Nội Dung
Hướng dẫn giải Bài 3. Phép cộng và phép trừ đa thức một biến sgk Toán 7 tập 2 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 5 6 7 8 9 trang 35 36 sgk Toán 7 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
BÀI 3. PHÉP CỘNG VÀ PHÉP TRỪ ĐA THỨC MỘT BIẾN
Hoạt động khởi động trang 33 Toán 7 tập 2 CTST
Có thể cộng và trừ hai đa thức một biến như cộng và trừ hai số thực không?
Trả lời:
Ta có thể cộng và trừ hai đa thức một biến như cộng và trừ hai số thực.
1. PHÉP CỘNG HAI ĐA THỨC MỘT BIẾN
Hoạt động khám phá 1 trang 33 Toán 7 tập 2 CTST
Hãy lập biểu thức biểu thị tổng chu vi hình vuông (Hình 1a) và hình chữ nhật (Hình 1b).

Trả lời:
Chu vi hình vuông là \(4x\)
Chu vi hình chữ nhật là \(2.[x+(x + 1)]\)
⇒ Tổng chu vi 2 hình là:
\({4x}+2.[x.(x + 1)] = 4x + 2(2x+1)\\= 4x +4x + 2 = 8x+2\).
Thực hành 1 trang 34 Toán 7 tập 2 CTST
Cho hai đa thức \(P(x) = 7{x^3} – 8x + 12\) và \(Q(x) = 6{x^2} – 2{x^3} + 3x – 5\). Hãy tính $P(x) + Q(x)$ bằng hai cách.
Trả lời:
♦ Cách 1:
$P(x) + Q(x)$
$= 7{x^3} – 8x + 12 + 6{x^2} – 2{x^3} + 3x – 5$
$= (7{x^3} – 2{x^3}) + 6{x^2} + ( – 8x + 3x) + (12 – 5)$
$= 5{x^3} + 6{x^2} – 5x + 7$
♦ Cách 2: đặt tính
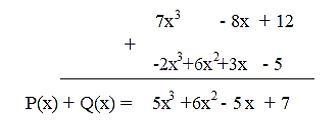
2. PHÉP TRỪ HAI ĐA THỨC MỘT BIẾN
Hoạt động khám phá 2 trang 34 Toán 7 tập 2 CTST
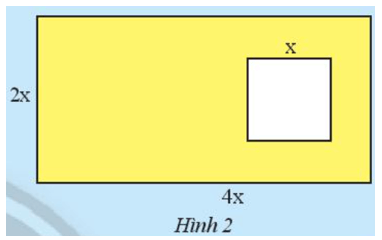
Hình 2 gồm một hình chữ nhật có chiều dài 4x cm, chiều rộng 2x cm và hình vuông nhỏ bên trong có cạnh x cm.
Hãy lập biểu thức biểu thị diện tích của phần được tô màu vàng trong Hình 2.
Trả lời:
Diện tích hình chữ nhật là \(2x.4x = 8{x^2}\)
Diện tích phần hình vuông là \({x^2}\)
Diện tích phần màu vàng còn lại là:
\(8{x^2} – {x^2} = 7{x^2}\)
Thực hành 2 trang 35 Toán 7 tập 2 CTST
Cho hai đa thức \(P(x) = 2{x^3} – 9{x^2} + 5\) và \(Q(x) = 2{x^2} + 4{x^3} – 7x\). Hãy tính $P(x) – Q(x)$ bằng hai cách.
Trả lời:
♦ Cách 1:
$P(x) – Q(x)$
$= 2x^3 – 9x^2 + 5 – (2x^2 + 4x^3 – 7x)$
$= 2x^3 – 9x^2 + 5 – 2x^2 – 4x^3 + 7x$
$= (2x^3 – 4x^3) + (-9x^2 – 2x^2) + 7x + 5$
$= -2x^3 – 11x^2 + 7x + 5$
♦ Cách 2: đặt tính
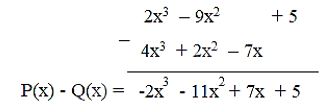
3. TÍNH CHẤT CỦA PHÉP CỘNG ĐA THỨC MỘT BIẾN
Thực hành 3 trang 35 Toán 7 tập 2 CTST
Thực hiện phép tính \((x – 4) + \left[ {({x^2} + 2x) + (7 – x)} \right]\).
Trả lời:
Bỏ dấu ngoặc rồi nhóm các đơn thức cùng lũy thừa, ta được:
$(x – 4) + \left[ {({x^2} + 2x) + (7 – x)} \right]$
$= x – 4 + ({x^2} + 2x + 7 – x)$
$= x – 4 + {x^2} + 2x + 7 – x$
$= {x^2} + (x + 2x – x) + ( – 4 + 7)$
$= {x^2} + 2x + 3$.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 7 8 9 trang 35 36 sgk Toán 7 tập 2 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 35 Toán 7 tập 2 CTST
Cho hai đa thức \(P(x) = – 3{x^4} – 8{x^2} + 2x\) và \(Q(x) = 5{x^3} – 3{x^2} + 4x – 6\).
Hãy tính $P(x) + Q(x)$ và $P(x) – Q(x)$.
Bài giải:
• Ta có:
$P(x) + Q(x)$
$= – 3{x^4} – 8{x^2} + 2x + 5{x^3} – 3{x^2} + 4x – 6$
\(= – 3{x^4} + 5{x^3} + (- 8{x^2} – 3{x^2}) + (2x + 4x) – 6\)
\(= – 3{x^4} + 5{x^3} – 11{x^2} + 6x – 6\)
Vậy \(P(x) + Q(x) = – 3{x^4} + 5{x^3} – 11{x^2} + 6x – 6\).
• Ta có:
$P(x) – Q(x)$
$= – 3{x^4} – 8{x^2} + 2x – 5{x^3} + 3{x^2} – 4x + 6$
\(= – 3{x^4} – 5{x^3} + ( – 8{x^2} + 3{x^2}) + (2x – 4x) + 6\)
\(= – 3{x^4} – 5{x^3} – 5{x^2} – 2x + 6\)
Vậy \(P(x) – Q(x) = – 3{x^4} – 5{x^3} – 5{x^2} – 2x + 6\).
Giải bài 2 trang 35 Toán 7 tập 2 CTST
Cho đa thức \(M(x) = 7{x^3} – 2{x^2} + 8x + 4\).
Tìm đa thức $N(x)$ sao cho $M(x) + N(x) = 3{x^2} – 2x$.
Bài giải:
Ta có:
$M(x) + N(x) = 3{x^2} – 2x$
$M(x) = 7{x^3} – 2{x^2} + 8x + 4$
Do đó:
$N(x) = M(x) + N(x) – M(x)$
\(= 3{x^2} – 2x – 7{x^3} + 2{x^2} – 8x – 4\)
\(= – 7{x^3} + 5{x^2} – 10x – 4\)
Vậy $N(x) = – 7{x^3} + 5{x^2} – 10x – 4$.
Giải bài 3 trang 36 Toán 7 tập 2 CTST
Cho đa thức \(A(y) = – 5{y^4} – 4{y^2} + 2y + 7\).
Tìm đa thức $B(y)$ sao cho \(B(y) – A(y) = 2{y^3} – 9{y^2} + 4y\).
Bài giải:
Ta có:
\(B(y) – A(y) = 2{y^3} – 9{y^2} + 4y\)
$A(y) = – 5{y^4} – 4{y^2} + 2y + 7$
Do đó:
$⇒ B(y) = 2{y^3} – 9{y^2} + 4y – 5{y^4} – 4{y^2} + 2y + 7$
$= – 5{y^4} + 2{y^3} – 13{y^2} + 6y + 7$
Vậy $B(y) = – 5{y^4} + 2{y^3} – 13{y^2} + 6y + 7$.
Giải bài 4 trang 36 Toán 7 tập 2 CTST
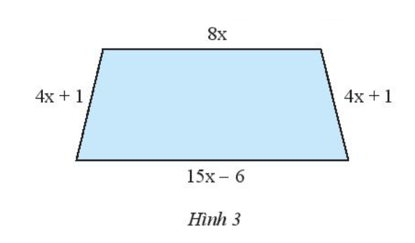
Viết biểu thức biểu thị chu vi của hình thang cân trong Hình 3.
Bài giải:
Chu vi của hình thang cân là:
\(C = 8x + (15x – 6) + (4x + 1) + (4x + 1)\)
\(= 31x – 4\)
Vậy biểu thức biểu thị chu vi của hình thang cân là $31x – 4$.
Giải bài 5 trang 36 Toán 7 tập 2 CTST
Cho tam giác (Hình 4) có chu vi bằng $12t – 3$. Tìm cạnh chưa biết của tam giác đó.
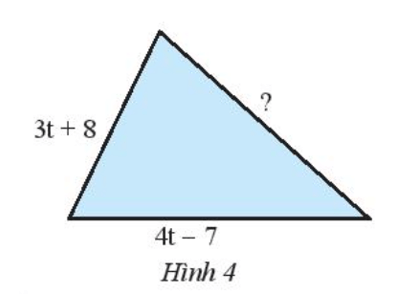
Bài giải:
Ta có:
Chu vi hình tam giác là: $12t – 3$
⇒ Cạnh cần tìm là:
$12t – 3 – (3t + 8) – (4t – 7) = 5t – 4$
Vậy độ dài cạnh còn lại của tam giác bằng $5t – 4$.
Giải bài 6 trang 36 Toán 7 tập 2 CTST
Cho ba đa thức \(P(x) = 9{x^4} – 3{x^3} + 5x – 1\).
\(Q(x) = – 2{x^3} – 5{x^2} + 3x – 8\) và \(R(x) = – 2{x^4} + 4{x^2} + 2x – 10\).
Tính $P(x) + Q(x) + R(x)$ và $P(x) – Q(x) – R(x)$.
Bài giải:
• Ta có:
$P(x)+Q(x)+R(x)$
$= 9{x^4} – 3{x^3} + 5x – 1 – 2{x^3} – 5{x^2} + 3x – 8 – 2{x^4} + 4{x^2} + 2x – 10$
$= (9{x^4} – 2{x^4}) + (- 3{x^3} – 2{x^3}) + (- 5{x^2} + 4{x^2}) +(5x + 3x + 2x) + (- 8 – 10 – 1)$
$= 7{x^4} – 5{x^3} – {x^2} + 10x – 19$
Vậy $P(x)+Q(x)+R(x) = 7{x^4} – 5{x^3} – {x^2} + 10x – 19$.
• Ta có:
$P(x)-Q(x)-R(x)$
$= 9{x^4} – 3{x^3} + 5x – 1 + 2{x^3} + 5{x^2} – 3x + 8 + 2{x^4} – 4{x^2} – 2x + 10$
$= (9{x^4} + 2{x^4}) + (- 3{x^3} + 2{x^3}) + (5{x^2} – 4{x^2}) + (5x – 3x – 2x) + (10 – 1 + 8)$
$= 11{x^4} – {x^3} + {x^2} + 17$
Vậy $P(x)-Q(x)-R(x) = 11{x^4} – {x^3} + {x^2} + 17$.
Giải bài 7 trang 36 Toán 7 tập 2 CTST
Cho đa thức \(P(x) = {x^3} – 4{x^2} + 8x – 2\). Hãy viết $P(x)$ thành tổng của hai đa thức bậc bốn.
Bài giải:
Ta thấy trong đa thức P(x) chưa có hạng tử thức bậc 4 nên ta sẽ thêm đơn thức bậc 4 vào đa thức sao cho kết quả của đa thức là không đổi.
Do đó:
$P(x) = {x^3} – 4{x^2} + 8x – 2$
$= {x^3} – 4{x^2} + 8x – 2 + {x^4} – {x^4}$
$= {x^4} + {x^3} – 4{x^2} + 8x – 2 – {x^4}$
$= ({x^4} + {x^3} – 4{x^2} + 8x – 2) + (- {x^4})$
Hoặc có thể viết tổng của hai đa thức sau:
$P(x) = (x^4 + x^3 – 4x^2) + (-x^4 + 8x – 2)$
Giải bài 8 trang 36 Toán 7 tập 2 CTST
Cho hình vuông cạnh 2x và bên trong là hình chữ nhật có độ dài hai cạnh là x và 3 (Hình 5).
Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh
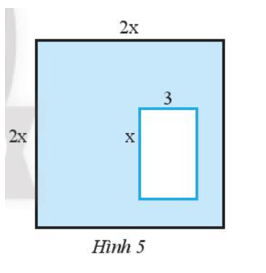
Bài giải:
Ta có:
Diện tích hình vuông là \(2x.2x = 4{x^2}\)
Diện tích hình chữ nhật là \(3.x = 3x\)
⇒ Diện tích phần cần tìm là: \(4{x^2} – 3x\)
Vậy biểu thức biểu thị diện tích của phần được tô màu xanh là \(4{x^2} – 3x\).
Giải bài 9 trang 36 Toán 7 tập 2 CTST
a) Thực hiện phép tính: \((3x – 1) + \left[ {(2{x^2} + 5x) + (4 – 3x)} \right]\).
b) Cho $A = 4x + 2, C = 5 – 3{x^2}$. Tìm đa thức $B$ sao cho $A + B = C$.
Bài giải:
a) Ta có:
$(3x – 1) + \left[ {(2{x^2} + 5x) + (4 – 3x)} \right]$
$= 3x – 1 + 2{x^2} + 5x + 4 – 3x$
$= 2{x^2}+( 3x +5x- 3x )+ (4 – 1)$
$= 2{x^2} + 5x + 3$
b) Vì $A + B = C$ nên $B = C – A$
Thay vào ta được:
\(B = 5 – 3{x^2} – 4x – 2\)
\(= – 3{x^2} – 4x + 3\)
Vậy $B = – 3{x^2} – 4x + 3$.
Bài trước:
👉 Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 trang 31 32 sgk Toán 7 tập 2 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 trang 40 sgk Toán 7 tập 2 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 trang 35 36 sgk Toán 7 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
