Nội Dung
Hướng dẫn giải Bài §3. Hằng đẳng thức đáng nhớ sgk Toán 8 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 6 trang 23 sgk Toán 8 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
§3. HẰNG ĐẲNG THỨC ĐÁNG NHỚ
Câu hỏi khởi động trang 18 Toán 8 tập 1 CD
Diện tích của hình vuông MNPQ (Hình 4) có thể được tính theo những cách nào?
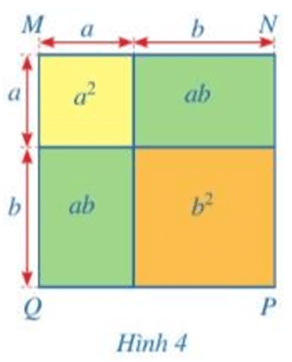
Trả lời:
♦ Cách 1:
Diện tích hình vuông MNPQ là:
\({a^2} + ab + ab + {b^2} = {a^2} + 2{\rm{a}}b + {b^2}\)
♦ Cách 2:
Độ dài cạnh của hình vuông MNPQ là: \(a + b\)
⇒ Diện tích của hình vuông MNPQ là:
\(\left( {a + b} \right).\left( {a + b} \right) = {\left( {a + b} \right)^2}\)
I. HẰNG ĐẲNG THỨC
Hoạt động 1 trang 18 Toán 8 tập 1 CD
Xét hai biểu thức: \(P = 2\left( {x + y} \right)\) và \(Q = 2{\rm{x}} + 2y\).
Tính giá trị của mỗi biểu thức P và Q rồi so sánh hai giá trị đó trong mỗi trường hợp sau:
a) Tại $x = 1; y = -1$;
b) Tại $x = 2; y = -3$.
Trả lời:
a) ♦ Thay $x = 1; y = -1$ vào biểu thức P ta được:
\(P = 2.\left[ {1 + \left( { – 1} \right)} \right] = 0\)
♦ Thay $x = 1; y = -1$ vào biểu thức Q ta được:
\(Q = 2.1 + 2.\left( { – 1} \right) = 0\)
\(\Rightarrow\) Tại $x = 1; y = -1, P = Q$.
b) ♦ Thay $x = 2; y = 3$ vào biểu thức P ta được:
\(P = 2.\left( {2 + 3} \right) = 10\)
♦ Thay $x = 2; y = 3$ vào biểu thức Q ta được:
\(Q = 2.2 + 2.3 = 10\)
\(\Rightarrow\) Tại $x = 2; y = 3, P = Q$.
Luyện tập vận dụng 1 trang 18 Toán 8 tập 1 CD
Chứng minh rằng: \(x\left( {x{y^2} + y} \right) – y\left( {{x^2}y + x} \right) = 0\).
Trả lời:
Ta có:
$x\left( {x{y^2} + y} \right) – y\left( {{x^2}y + x} \right)$
$= x.x{y^2} + xy – y.{x^2}y – {\rm{yx}}$
$= {x^2}{y^2} + xy – {x^2}{y^2} – xy$
$= \left( {{x^2}{y^2} – {x^2}{y^2}} \right) + \left( {xy – xy} \right) = 0$
Vậy \(x\left( {x{y^2} + y} \right) – y\left( {{x^2}y + x} \right) = 0\) (đpcm)
II. HẰNG ĐẲNG THỨC ĐÁNG NHỚ
Hoạt động 2 trang 18 Toán 8 tập 1 CD
Với a, b là hai số thực bất kì, thực hiện phép tính:
a) \(\left( {a + b} \right)\left( {a + b} \right)\);
b) \(\left( {a – b} \right)\left( {a – b} \right)\).
Trả lời:
a) Ta có:
$\left( {a + b} \right)\left( {a + b} \right) = a.a + ab + ab + b.b$
$= {a^2} + 2{\rm{a}}b + {b^2}$
b) Ta có:
$\left( {a – b} \right)\left( {a – b} \right) = a.a – a.b – a.b – b.\left( { – b} \right)$
$= {a^2} – 2{\rm{a}}b + {b^2}$
Luyện tập vận dụng 2 trang 19 Toán 8 tập 1 CD
Tính:
a) \({\left( {x + \dfrac{1}{2}} \right)^2}\);
b) \({\left( {2{\rm{x}} + y} \right)^2}\);
c) \({\left( {3 – x} \right)^2}\);
d) \({\left( {x – 4y} \right)^2}\).
Trả lời:
a) Ta có:
${\left( {x + \dfrac{1}{2}} \right)^2} = {x^2} + 2.x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2}$
$= {x^2} + x + \dfrac{1}{4}$
b) Ta có:
${\left( {2{\rm{x}} + y} \right)^2} = {\left( {2{\rm{x}}} \right)^2} + 2.2{\rm{x}}.y + {y^2}$
$= 4{{\rm{x}}^2} + 4{\rm{x}}y + {y^2}$
c) Ta có:
${\left( {3 – x} \right)^2} = {3^2} – 2.3.x + {x^2}$
$= 9 – 6{\rm{x}} + {x^2}$
d) Ta có:
${\left( {x – 4y} \right)^2} = {x^2} – 2.x.4y + {\left( {4y} \right)^2}$
$= {x^2} – 8{\rm{x}}y + 16{y^2}$
Luyện tập vận dụng 3 trang 19 Toán 8 tập 1 CD
Với mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
a) \({y^2} + y + \dfrac{1}{4}\);
b) \({y^2} + 49 – 14y\).
Trả lời:
a) Ta có:
${y^2} + y + \dfrac{1}{4} = {y^2} – 2.y.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2}$
$= {\left( {y – \dfrac{1}{2}} \right)^2}$
b) Ta có:
${y^2} + 49 – 14y = {y^2} – 14y + 49$
$= {y^2} – 2.y.7 + {7^2} = {\left( {y – 7} \right)^2}$
Luyện tập vận dụng 4 trang 19 Toán 8 tập 1 CD
Tính nhanh: \({49^2}\).
Trả lời:
Ta có:
${49^2} = {\left( {50 – 1} \right)^2}$
$= {50^2} – 2.50.1 + {1^2}$
$= 2500 – 100 – 1$
$= 2401$
Vậy: \({49^2} = 2401\)
Hoạt động 3 trang 19 Toán 8 tập 1 CD
Với $a, b$ là hai số thực bất kì, thực hiện phép tính: \(\left( {a – b} \right)\left( {a + b} \right)\).
Trả lời:
Ta có:
\(\left( {a – b} \right)\left( {a + b} \right) = a.a + a.b – ba – b.b = {a^2} – {b^2}\)
Luyện tập vận dụng 5 trang 20 Toán 8 tập 1 CD
Viết mỗi biểu thức sau dưới dạng tích:
a) \(9{{\rm{x}}^2} – 16\);
b) \(25 – 16{y^2}\).
Trả lời:
a) Ta có:
\(9{{\rm{x}}^2} – 16 = {\left( {3{\rm{x}}} \right)^2} – {4^2} = \left( {3{\rm{x}} – 4} \right)\left( {3{\rm{x}} + 4} \right)\)
b) Ta có:
\(25 – 16{y^2} = {5^2} – {\left( {4y} \right)^2} = \left( {5 – 4y} \right)\left( {5 + 4y} \right)\)
Luyện tập vận dụng 6 trang 20 Toán 8 tập 1 CD
Tính:
a) \(\left( {a – 3b} \right)\left( {a + 3b} \right)\);
b) \(\left( {2{\rm{x}} + 5} \right)\left( {2{\rm{x}} – 5} \right)\);
c) \(\left( {4y – 1} \right)\left( {4y + 1} \right)\).
Trả lời:
a) Ta có:
\(\left( {a – 3b} \right)\left( {a + 3b} \right) = {a^2} – {\left( {3b} \right)^2} = {a^2} – 9{b^2}\)
b) Ta có:
\(\left( {2{\rm{x}} + 5} \right)\left( {2{\rm{x}} – 5} \right) = {\left( {2{\rm{x}}} \right)^2} – {5^2} = 4{{\rm{x}}^2} – 25\)
c) Ta có:
\(\left( {4y – 1} \right)\left( {4y + 1} \right) = {\left( {4y} \right)^2} – {1^2} = 16{y^2} – 1\)
Luyện tập vận dụng 7 trang 20 Toán 8 tập 1 CD
Tính nhanh: \(48.52\).
Trả lời:
Ta có:
$48.52 = \left( {50 – 2} \right)\left( {50 + 2} \right)$
$= {50^2} – {2^2} = 2500 – 4$
$= 2496$.
Hoạt động 4 trang 20 Toán 8 tập 1 CD
Với a, b là hai số thực bất kì, thực hiện phép tính:
a) \(\left( {a + b} \right){\left( {a + b} \right)^2}\);
b) \(\left( {a – b} \right){\left( {a – b} \right)^2}\).
Trả lời:
a) Ta có:
$\left( {a + b} \right){\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {{a^2} + 2{\rm{a}}b + {b^2}} \right)$
$= {a^3} + 2{{\rm{a}}^2}b + a{b^2} + b{a^2} + 2{\rm{a}}{b^2} + {b^3}$
$= {a^3} + 3{{\rm{a}}^2}b + 3{\rm{a}}{b^3} + {b^3}$
b) Ta có:
$\left( {a – b} \right){\left( {a – b} \right)^2} = \left( {a – b} \right)\left( {{a^2} – 2{\rm{a}}b + {b^2}} \right)$
$= {a^3} – 2{{\rm{a}}^2}b + a{b^2} – b{a^2} + 2{\rm{a}}{b^2} – {b^3}$
$= {a^3} – 3{{\rm{a}}^2}b + 3{\rm{a}}{b^3} – {b^3}$
Luyện tập vận dụng 8 trang 21 Toán 8 tập 1 CD
Tính:
\(a){\left( {3 + x} \right)^3}\);
\(b){\left( {a + 2b} \right)^3}\);
\(c){\left( {2{\rm{x}} – y} \right)^3}\).
Trả lời:
a) Ta có:
${\left( {3 + x} \right)^3} = {3^3} + {3.3^2}x + 3.3.{x^2} + {x^3}$
$= 27 + 27{\rm{x}} + 9{{\rm{x}}^2} + {x^3}$
b) Ta có:
${\left( {a + 2b} \right)^3} = {a^3} + 3{{\rm{a}}^2}.\left( {2b} \right) + 3{\rm{a}}.{\left( {2b} \right)^2} + {\left( {2b} \right)^3}$
$= {a^3} + 6{{\rm{a}}^2}b + 12{\rm{a}}{b^2} + 8{b^3}$
c) Ta có:
${\left( {2{\rm{x}} – y} \right)^3} = {\left( {2{\rm{x}}} \right)^3} – 3.{\left( {2{\rm{x}}} \right)^2}y + 3.2{\rm{x}}.{y^2} + {y^3}$
$= 8{{\rm{x}}^3} – 12{{\rm{x}}^2}y + 6{\rm{x}}{y^2} + {y^3}$
Luyện tập vận dụng 9 trang 21 Toán 8 tập 1 CD
Viết biểu thức sau dưới dạng lập phương của một hiệu:
\(8{{\rm{x}}^3} – 36{{\rm{x}}^2}y + 54{\rm{x}}{y^2} – 27{y^3}\).
Trả lời:
Ta có:
$8{{\rm{x}}^3} – 36{{\rm{x}}^2}y + 54{\rm{x}}{y^2} – 27{y^3}$
$= {\left( {2{\rm{x}}} \right)^3} – 3.\left( {2{\rm{x}}} \right).3y + 3.2{\rm{x}}.{\left( {3y} \right)^2} – {\left( {3y} \right)^3}$
$= {\left( {2{\rm{x}} – 3y} \right)^3}$
Luyện tập vận dụng 10 trang 21 Toán 8 tập 1 CD
Tính nhanh: \({101^3} – {3.101^2} + 3.101 – 1\).
Trả lời:
Ta có:
${101^3} – {3.101^2} + 3.101 – 1$
$= {101^3} – {3.101^2}.1 + {3.101.1^2} – {1^3}$
$= {\left( {101 – 1} \right)^3} = {100^3}$
Hoạt động 5 trang 21 Toán 8 tập 1 CD
Với a, b là hai số thực bất kì, thực hiện phép tính:
a) \(\left( {a + b} \right)\left( {{a^2} – ab + {b^2}} \right)\);
b) \(\left( {a – b} \right)\left( {{a^2} + ab + {b^2}} \right)\).
Trả lời:
a) Ta có:
$\left( {a + b} \right)\left( {{a^2} – ab + {b^2}} \right)$
$= {a^3} – {a^2}b + a{b^2} + b{a^2} – a{b^2} + {b^3}$
$= {a^3} + {b^3}$
b) Ta có:
$\left( {a – b} \right)\left( {{a^2} + ab + {b^2}} \right)$
$= {a^3} + {a^2}b + a{b^2} – b{a^3} – a{b^3} – {b^3}$
$= {a^3} – {b^3}$
Luyện tập vận dụng 11 trang 22 Toán 8 tập 1 CD
Viết mỗi biểu thức sau dưới dạng tích:
a) \(27{{\rm{x}}^3} + 1\);
b) \(64 – 8{y^3}\).
Trả lời:
a) Ta có:
$27{{\rm{x}}^3} + 1 = {\left( {3{\rm{x}}} \right)^3} + 1$
$= \left( {3{\rm{x}} + 1} \right).\left[ {{{\left( {3{\rm{x}}} \right)}^2} – 3{\rm{x}}.1 + {1^2}} \right] $
$= \left( {3{\rm{x}} + 1} \right)\left( {9{{\rm{x}}^2} – 3{\rm{x}} + 1} \right)$
b) Ta có:
$64 – 8{y^3} = {4^3} – {\left( {2y} \right)^3}$
$= \left( {4 – 2y} \right)\left[ {{4^2} + 4.2y + {{\left( {2y} \right)}^2}} \right]$
$= \left( {4 – 2y} \right)\left( {16 + 8y + 4{y^2}} \right)$
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 trang 23 sgk Toán 8 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 23 Toán 8 tập 1 CD
Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
a) \(4{{\rm{x}}^2} + 28{\rm{x}} + 49\);
b) \(4{{\rm{a}}^2} + 20{\rm{a}}b + 25{b^2}\);
c) \(16{y^2} – 8y + 1\);
d) \(9{{\rm{x}}^2} – 6{\rm{x}}y + {y^2}\).
Bài giải:
a) Ta có:
\(4{{\rm{x}}^2} + 28{\rm{x}} + 49 \\= {\left( {2{\rm{x}}} \right)^2} + 2.2{\rm{x}}.7 + {7^2} \\= {\left( {2{\rm{x}} + 7} \right)^2}\)
b) Ta có:
\(4{{\rm{a}}^2} + 20{\rm{a}}b + 25{b^2} \\= {\left( {2{\rm{a}}} \right)^2} + 2.2{\rm{a}}.5b + {\left( {5b} \right)^2} \\= {\left( {2{\rm{a}} + 5b} \right)^2}\)
c) Ta có:
\(16{y^2} – 8y + 1 \\= {\left( {4y} \right)^2} – 2.4y.1 + {1^2} \\= {\left( {4y – 1} \right)^2}\)
d) Ta có:
\(9{{\rm{x}}^2} – 6{\rm{x}}y + {y^2} \\= {\left( {3{\rm{x}}} \right)^2} – 2.3{\rm{x}}.y + {y^2} \\= {\left( {3{\rm{x}} – y} \right)^2}\)
Giải bài 2 trang 23 Toán 8 tập 1 CD
Viết mỗi biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu:
a) \({a^3} + 12{{\rm{a}}^2} + 48{\rm{a}} + 64\);
b) \(27{{\rm{x}}^3} + 54{{\rm{x}}^2}y + 36{\rm{x}}{y^2} + 8{y^3}\);
c) \({x^3} – 9{{\rm{x}}^2} + 27{\rm{x}} – 27\);
d) \(8{{\rm{a}}^3} – 12{{\rm{a}}^2}b + 6{\rm{a}}{b^2} – {b^3}\).
Bài giải:
a) Ta có:
\({a^3} + 12{{\rm{a}}^2} + 48{\rm{a}} + 64 \\= {a^3} + 3{{\rm{a}}^2}.4 + 3{\rm{a}}{.4^2} + {4^3} \\= {\left( {a + 4} \right)^3}\)
b) Ta có:
\(27{{\rm{x}}^3} + 54{{\rm{x}}^2}y + 36{\rm{x}}{y^2} + 8{y^3}\\= {\left( {3{\rm{x}}} \right)^3} + 3.{\left( {3{\rm{x}}} \right)^2}.2y + 3.3{\rm{x}}.{\left( {2y} \right)^2} + {\left( {2y} \right)^3} \\= {\left( {3{\rm{x}} + 2y} \right)^3}\)
c) Ta có:
\({x^3} – 9{{\rm{x}}^2} + 27{\rm{x}} – 27 \\= {x^3} – 3.{x^2}.3 + 3.x{.3^2} – {3^3} \\= {\left( {x – 3} \right)^3}\)
d) Ta có:
\(8{{\rm{a}}^3} – 12{{\rm{a}}^2}b + 6{\rm{a}}{b^2} – {b^3} \\= {\left( {2{\rm{a}}} \right)^2} – 3.{\left( {2{\rm{a}}} \right)^2}.b + 3.2{\rm{a}}.{b^2} – {b^3} \\= {\left( {2{\rm{a}} – b} \right)^3}\)
Giải bài 3 trang 23 Toán 8 tập 1 CD
Viết mỗi biểu thức sau dưới dạng tích:
a) \(25{{\rm{x}}^2} – 16\);
b) \(16{{\rm{a}}^2} – 9{b^2}\);
c) \(8{{\rm{x}}^3} + 1\);
d) \(125{{\rm{x}}^3} + 27{y^3}\);
e) \(8{{\rm{x}}^3} – 125\);
g) \(27{{\rm{x}}^3} – {y^3}\).
Bài giải:
a) Ta có:
\(25{{\rm{x}}^2} – 16 = {\left( {5{\rm{x}}} \right)^2} – {4^2} \\= \left( {5{\rm{x}} + 4} \right)\left( {5{\rm{x}} – 4} \right)\)
b) Ta có:
\(16{{\rm{a}}^2} – 9{b^2} = {\left( {4{\rm{a}}} \right)^2} – {\left( {3b} \right)^2} \\= \left( {4{\rm{a}} – 3b} \right)\left( {4{\rm{a}} + 3b} \right)\)
c) Ta có:
\(8{{\rm{x}}^3} + 1 = {\left( {2{\rm{x}}} \right)^3} + {1^3} \\= \left( {2{\rm{x}} + 1} \right)\left( {4{{\rm{x}}^2} – 2{\rm{x}} + 1} \right)\)
d) Ta có:
\(125{{\rm{x}}^3} + 27{y^3} = {\left( {5{\rm{x}}} \right)^3} + {\left( {3y} \right)^3} \\= \left( {5{\rm{x}} + 3y} \right)\left( {25{{\rm{x}}^2} – 15{\rm{x}}y + 9{y^2}} \right)\)
e) Ta có:
\(8{{\rm{x}}^3} – 125 = {\left( {2{\rm{x}}} \right)^3} – {5^3} \\= \left( {2{\rm{x}} – 5} \right)\left( {4{{\rm{x}}^2} + 10{\rm{x + }}25} \right)\)
g) Ta có:
\(27{{\rm{x}}^3} – {y^3} = {\left( {3x} \right)^3} – {y^3} \\= \left( {3{\rm{x}} – y} \right)\left( {9{{\rm{x}}^2} + 3{\rm{x}}y + {y^2}} \right)\)
Giải bài 4 trang 23 Toán 8 tập 1 CD
Tính giá trị của mỗi biểu thức:
a) \(A = {x^2} + 6{\rm{x}} + 10\) tại $x = -103$;
b) \(B = {x^3} + 6{{\rm{x}}^2} + 12{\rm{x}} + 12\) tại $x = 8$.
Bài giải:
a) Ta có:
\(A = {x^2} + 6{\rm{x}} + 10 \\= {x^2} + 2.x.3 + {3^2} + 1 \\= {\left( {x + 3} \right)^2} + 1\)
Thay $x = -103$ vào biểu thức A rút gọn ta được:
\(A = {\left( { – 103 + 3} \right)^2} + 1 = 10000 + 1 = 10001\)
Vậy $A = 10001$ tại $x = – 103$
b) Ta có:
\(B = {x^3} + 6{{\rm{x}}^2} + 12{\rm{x}} + 12 \\= {x^3} + 3.{x^2}.2 + 3.x{.2^2} + {2^3} + 4 \\= {\left( {x + 2} \right)^3} + 4\)
Thay $x = 8$ vào biểu thức B vừa rút gọn ta được:
\(B = {\left( {8 + 2} \right)^3} + 4 = {10^3} + 4 = 1004\)
Vậy $B = 1004$ tại $x = 8$.
Giải bài 5 trang 23 Toán 8 tập 1 CD
Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến x:
a) \(C = {\left( {3{\rm{x}} – 1} \right)^2} + {\left( {3{\rm{x}} + 1} \right)^2} – 2\left( {3{\rm{x}} – 1} \right)\left( {3{\rm{x}} + 1} \right)\);
b) \(D = {\left( {x + 2} \right)^3} – {\left( {x – 2} \right)^3} – 12\left( {{x^2} + 1} \right)\);
c) \(E = \left( {x + 3} \right)\left( {{x^2} – 3{\rm{x}} + 9} \right) – \left( {x – 2} \right)\left( {{x^2} + 2{\rm{x}} + 4} \right)\);
d) \(G = \left( {2{\rm{x}} – 1} \right)\left( {4{{\rm{x}}^2} + 2{\rm{x}} + 1} \right) – 8\left( {x + 2} \right)\left( {{x^2} – 2{\rm{x}} + 4} \right)\).
Bài giải:
a) Ta có:
$C = {\left( {3{\rm{x}} – 1} \right)^2} + {\left( {3{\rm{x}} + 1} \right)^2} – 2\left( {3{\rm{x}} – 1} \right)\left( {3{\rm{x}} + 1} \right)$
$= {\left( {3{\rm{x}} – 1} \right)^2} – 2\left( {3{\rm{x}} – 1} \right)\left( {3{\rm{x}} + 1} \right) + {\left( {3{\rm{x}} + 1} \right)^2}$
$= {\left( {3{\rm{x}} – 1 – 3{\rm{x}} – 1} \right)^2}$
$= {\left( { – 2} \right)^2} = 4$
Vậy giá trị của biểu thức $C = 4$ không phụ thuộc vào biến $x$.
b) Ta có:
$D = {\left( {x + 2} \right)^3} – {\left( {x – 2} \right)^3} – 12\left( {{x^2} + 1} \right)$
$= \left( {x + 2 – x + 2} \right)\left[ {{{\left( {x + 2} \right)}^2} + \left( {x + 2} \right)\left( {x – 2} \right) + {{\left( {x – 2} \right)}^2}} \right] – 12{{\rm{x}}^2} – 12$
$= 4.\left( {{x^2} + 4{\rm{x}} + 4 + {x^2} – 4 + {x^2} – 4{\rm{x}} + 4} \right) – 12{{\rm{x}}^2} – 12$
$= 4.\left( {3{{\rm{x}}^2} + 4} \right) – 12{{\rm{x}}^2} – 12$
$= 12{{\rm{x}}^2} + 16 – 12{{\rm{x}}^2} – 12 = 4$
Vậy giá trị của biểu thức $D = 4$ không phụ thuộc vào biến $x$.
c) Ta có:
$E = \left( {x + 3} \right)\left( {{x^2} – 3{\rm{x}} + 9} \right) – \left( {x – 2} \right)\left( {{x^2} + 2{\rm{x}} + 4} \right)$
$= \left( {{x^3} + {3^3}} \right) – \left( {{x^3} – {2^2}} \right)$
$= {x^3} + 27 – {x^3} + 8 = 35$
Vậy giá trị của biểu thức $E = 35$ không phụ thuộc vào biến $x$.
d) Ta có:
$G = \left( {2{\rm{x}} – 1} \right)\left( {4{{\rm{x}}^2} + 2{\rm{x}} + 1} \right) – 8\left( {x + 2} \right)\left( {{x^2} – 2{\rm{x}} + 4} \right)$
$= \left[ {{{\left( {2{\rm{x}}} \right)}^3} – {1^3}} \right] – 8\left( {{x^3} + {2^3}} \right)$
$= 8{{\rm{x}}^3} – 1 – 8{{\rm{x}}^3} – 64 = – 65$
Vậy giá trị của biểu thức $G = -65$ không phụ thuộc vào biến $x$.
Giải bài 6 trang 23 Toán 8 tập 1 CD
Tính nhanh: $(0,76)^3 + (0,24)^3 + 3 . 0,76 . 024$.
Bài giải:
Ta có:
$(0,76)^3 + (0,24)^3 + 3 . 0,76 . 024$
$= (0,76 + 0,24)^3 – 3 . 0,76 . 024 . (0,76 + 024) + 3 . 0,76 . 024$
$= 1^3 – 3 . 0,76 . 024 . 1 + 3 . 0,76 . 024$
$= 1 – 3 . 0,76 . 024 + 3 . 0,76 . 024 = 1$.
Vậy $(0,76)^3 + (0,24)^3 + 3 . 0,76 . 024 = 1$.
Bài trước:
👉 Giải bài 1 2 3 4 5 6 7 trang 16 17 sgk Toán 8 tập 1 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 trang 26 27 sgk Toán 8 tập 1 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 trang 23 sgk Toán 8 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
