Nội Dung
Hướng dẫn giải Bài §4. Đồ thị của hàm số bậc nhất y = ax + b (a≠0) sgk Toán 8 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 6 trang 77 sgk Toán 8 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
§4. ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT $y = ax + b (a ≠ 0)$
Câu hỏi khởi động trang 71 Toán 8 tập 1 CD
Ở bài học trước, ta đã học đồ thị của một hàm số trên mặt phẳng tọa độ. Trong bài học này, ta sẽ tìm hiểu một trường hợp riêng trong đồ thị của hàm số, đó là đồ thị của hàm số bậc nhất.
Đồ thị hàm số bậc nhất \(y = {\rm{ax + b}}\left( {a \ne 0} \right)\) có tính chất gì?
Trả lời:
Đồ thị hàm số bậc nhất \(y = {\rm{ax + b}}\left( {a \ne 0} \right)\) là một đường thẳng.
I. ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT
Hoạt động 1 trang 71 Toán 8 tập 1 CD
Xét hàm số: $y = x – 2$.
a) Tìm giá trị của y tương ứng với giá trị của $x$ trong bảng sau:
| $x$ | 0 | 2 | 3 |
| $y = x – 2$ | ? | ? | ? |
b) Vẽ các điểm $A (0; -2); B(2; 0); C(3; 1)$ của đồ thị hàm số $y = x – 2$ trong mặt phẳng tọa độ $Oxy$. Dùng thước thẳng để kiểm tra ba điểm $A, B, C$ có thẳng hàng hay không?
Trả lời:
a) Thay các giá trị $x = 0; x = 2; x = 3$ vào công thức đồ thị hàm số $y = x – 2$ ta được các giá trị $y$ tương ứng ở bảng sau:
| $x$ | 0 | 2 | 3 |
| $y$ | -2 | 0 | 1 |
b) Vẽ các điểm $A (0; -2); B(2; 0); C(3; 0)$

Kẻ đường thẳng qua điểm $A$ và $C$ ta thấy đường thẳng đi qua điểm $B$
Vậy ba điểm $A, B, C$ có thẳng hàng.
Luyện tập vận dụng 1 trang 72 Toán 8 tập 1 CD
Cho hàm số $y = 4x + 3$. Tìm điểm thuộc đồ thị hàm số của hàm số có hoành độ bằng $0$.
Trả lời:
Với $x = 0$ thì $y = 4.0 + 3 = 3$
Vậy điểm có hoành độ bằng $0$ thuộc đồ thị hàm số $y = 4x + 3$ là $(0; 3)$.
II. VẼ ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT
Luyện tập vận dụng 2 trang 73 Toán 8 tập 1 CD
Vẽ đồ thị của mỗi hàm số sau:
a) $y = 3x$;
b) $y = 2x + 2$.
Trả lời:
a) Hàm số $y = 3x$:
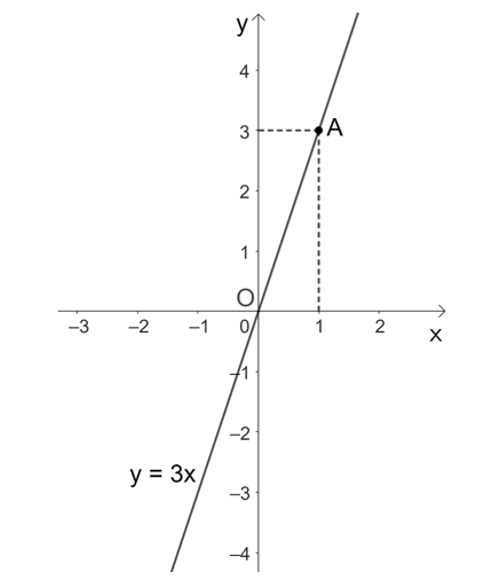
Với $x = 1$ thì $y = 3$ ta được điểm $A(1; 3)$ thuộc đồ thị hàm số $y = 3x$
Vậy đồ thị hàm số $y = 3x$ là đường thẳng đi qua $2$ điểm $O(0; 0)$ và $A(1; 3)$
Khi đó, đồ thị hàm số $y = 3x$ được biểu diễn như hình vẽ:
b) Hàm số $y = 2x + 2$:
Với $x = 0$ thì $y = 2$ ta được điểm $M(0; 2)$ thuộc đồ thị hàm số $y = 2x + 2$
Với $y = 0$ thì $x = -1$ ta được điểm $N(-1; 0)$ thuộc vào đồ thị hàm số $y = 2x + 2$
Vậy đồ thị hàm số $y = 2x + 2$ là đường thẳng đi qua điểm $M(0; 2)$ và $N(-1; 0)$
Khi đó, đồ thị hàm số $y = 2x + 2$ được biểu diễn như hình vẽ:

III. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG $y = ax + b (a ≠ 0)$
Hoạt động 2 trang 73 Toán 8 tập 1 CD
Quan sát các đường thẳng $y = x +1$ và $y = -x – 1$ (Hình 20).
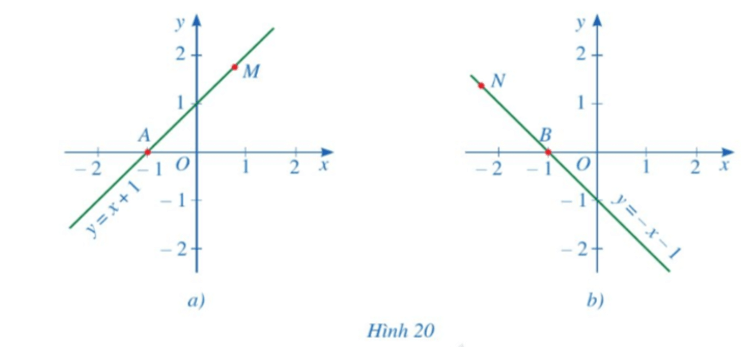
a) Tung độ các điểm $M, N$ là số dương hay số âm?
b) Tìm góc tạo bởi hai tia $Ax$ và $AM$ ở Hình 20a.
c) Tìm góc tạo bởi hai tia $Bx$ và $BN$ ở Hình 20b.
Trả lời:
a) Tung độ của điểm $M$ mang dấu dương.
Tung độ của điểm $N$ mang dấu dương
b) Góc tạo bởi hai tia $Ax$ và $AM$ là góc $MAO$.
c) Góc tạo bởi 2 tia $Bx$ và $BN$ là góc $NBO$.
Hoạt động 3 trang 74 Toán 8 tập 1 CD
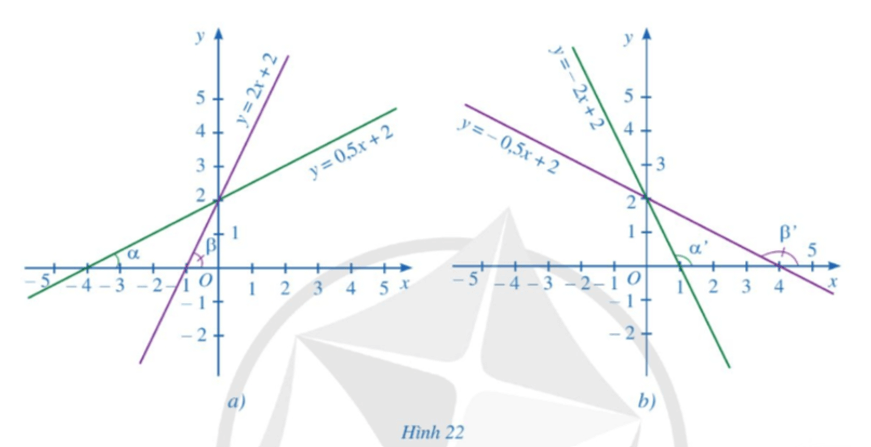
Hình 22a biểu diễn đồ thị của các hàm số bậc nhất: $y = 0,5x + 2; y = 2x + 2$. Hình 22b biểu diễn đồ thị của các hàm số bậc nhất: $y = -2x + 2; y = -0,5x + 2$.
a) Quan sát Hình 22a, so sánh các góc $α, β$ và so sánh các giá trị tương ứng của hệ số của $x$ trong các hàm số bậc nhất rồi rút ra nhận xét.
b) Quan sát Hình 22b, so sánh các góc $α’, β’$ và so sánh các giá trị tương ứng của hệ số của $x$ trong các hàm số bậc nhất rồi rút ra nhận xét.
Trả lời:
a) Quan sát Hình 22a ta thấy: \(\widehat \alpha < \widehat \beta \)
– Hệ số $x$ của hàm số $y = 0,5x + 2$ là $0,5$.
– Hệ số $x$ của hàm số $y = 2x + 2$ là $2$.
Từ đó ta suy ra: hệ số của $x$ trong các hàm số $y = 0,5x + 2$ nhỏ hơn hệ số của $x$ của đường thẳng $y = 2x + 2$.
Nhận xét:
• Khi hệ số của $x$ lớn hơn $0$ thì góc tạo bởi đường thẳng đó với trục $Ox$ là góc nhọn.
• Hệ số của $x$ càng nhỏ thì góc tạo bởi đường thẳng đó với trục $Ox$ càng nhỏ.
b) Quan sát Hình 22b ta thấy: \(\widehat {\alpha ‘} < \widehat {\beta ‘}\)
– Hệ số $x$ của hàm số $y = -0,5 x + 2$ là $-0,5$
– Hệ số $x$ của hàm số $y = -2x + 2$ là $-2$.
Ta thấy: $- 0,5 > -2$
Từ đó ta suy ra: hệ số của $x$ trong các hàm số $y = – 2x + 2$ nhỏ hơn hệ số của $x$ của đường thẳng $y = – 0,5x + 2$.
Nhận xét:
• Khi hệ số của $x$ nhỏ hơn $0$ thì góc tạo bởi đường thẳng đó với trục $Ox$ là góc tù.
• Hệ số của $x$ càng nhỏ thì góc tạo bởi đường thẳng đó với trục $Ox$ càng lớn.
Luyện tập vận dụng 3 trang 75 Toán 8 tập 1 CD
Tìm hệ số góc của đường thẳng $y = -5x + 11$.
Trả lời:
Hệ số góc của đường thẳng $y = -5x + 11$ là $-5$.
Hoạt động 4 trang 76 Toán 8 tập 1 CD
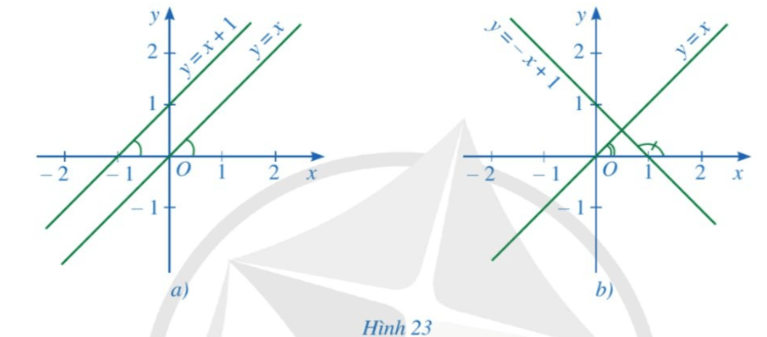
a) Quan sát Hình 23a, tìm hệ số góc của hai đường thẳng $y = x$ và $y = x + 1$ và nêu vị trí tương đối của hai đường thẳng đó.
b) Quan sát Hình 23b, tìm hệ số góc của hai đường thẳng $y = x$ và $y = – x + 1$ và nêu vị trí tương đối của hai đường thẳng đó.
Trả lời:
a) Hệ số góc của đường thẳng $y = x$ là $1$
Hệ số góc của đường thẳng $y = x + 1$ là $1$
⇒ Hai đường thẳng $y = x$ và $y = x + 1$ song song với nhau.
b) Hệ số góc của đường thẳng $y = x$ là $1$
Hệ số góc của đường thẳng $y = -x + 1$ là $-1$
⇒ Hai đường thẳng $y = x$ và $y = -x + 1$ cắt nhau.
Luyện tập vận dụng 4 trang 76 Toán 8 tập 1 CD
Xét vị trí tương đối của hai đường thẳng $y = -5x$ và $y = -5x +2$.
Trả lời:
Hai đường thẳng $y = -5x$ và $y = -5x +2$ có hệ số góc bằng nhau và hệ số tự do khác nhau nên hai đường thẳng đó song song với nhau.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 trang 77 sgk Toán 8 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 77 Toán 8 tập 1 CD
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về hai đường thẳng $d$ là đồ thị của hàm số $y = ax + b \left( {a \ne 0} \right)$?
a) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng \( – \dfrac{b}{a}\);
b) Đường thẳng d cắt trục tung tại điểm có tung độ bằng \( – \dfrac{b}{a}\);
c) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b;
d) Đường thẳng d cắt trục tung tại điểm có tung độ bằng b.
Bài giải:
Ta có:
• Đường thẳng $d$ cắt trục tung, tức là $y = 0$ nên ta có: $ax + b = 0$.
Suy ra $ax = – b$ hay $x = – \dfrac{b}{a}$
Khi đó, đường thẳng $d$ cắt trục tung tại điểm có tung độ bằng $- \dfrac{b}{a}$
• Đường thẳng $d$ cắt trục hoành, tức là $x = 0$ nên ta có: $y = a . 0 + b = 0 + b = b$.
Khi đó, đường thẳng $d$ cắt trục hoành tại điểm có hoành độ bằng $b$.
Do đó:
a) Sai
b) Đúng
c) Đúng
d) Sai
Giải bài 2 trang 77 Toán 8 tập 1 CD
Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong số các đường thẳng sau:
$y = -2x + 5; y = -2x; y = 4x -1$.
Bài giải:
• Đường thẳng $y = – 2x + 5$ có hệ số góc bằng $– 2$ và hệ số tự do bằng $5$.
• Đường thẳng $y = – 2x$ có hệ số góc bằng $– 2$ và hệ số tự do bằng $0$.
• Đường thẳng $y = 4x – 1$ có có hệ số góc bằng $4$ và hệ số tự do bằng$ – 1$.
Do đó:
Hai đường thẳng $y = – 2x + 5$ và $y = – 2x$ có hệ số góc bằng nhau và hệ số tự do khác nhau nên hai đường thẳng này song song.
Hai đường thẳng $y = – 2x + 5$ và $y = 4x – 1$ có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.
Hai đường thẳng $y = – 2x$ và $y = 4x – 1$ có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.
Vậy các cặp đường thẳng cắt nhau là: $y = – 2x + 5$ và $y = 4x – 1$; $y = – 2x$ và $y = 4x – 1$; các cặp đường thẳng song song là $y = – 2x + 5$ và $y = – 2x$.
Giải bài 3 trang 77 Toán 8 tập 1 CD
Vẽ đồ thị các hàm số \(y = 3{\rm{x}};y = 3{\rm{x}} + 4;y = – \dfrac{1}{2}x;y = – \dfrac{1}{2}x + 3\) trên cùng một mặt phẳng tọa độ.
Bài giải:
♦ Hàm số $y = 3x$:
Với $x = 1$ thì $y = 3$, ta được điểm $A(1; 3)$ thuộc đồ thị hàm số $y = 3x$
Vậy đồ thị hàm số $y = 3x$ là đường thẳng đi qua hai điểm $O(0; 0)$ và $A(1; 3)$
♦ Hàm số $y = 3x + 4$:
Với $x = 0$ thì $y = 4$, ta được điểm $B(0; 4)$ thuộc đồ thị hàm số $y = 3x + 4$
Với $x = -1$ thì $y = 1$, ta được điểm $C(-1; 1)$ thuộc đồ thị hàm số $y = 3x + 4$
Vậy đồ thị hàm số $y = 3x + 4$ là đường thẳng đi qua hai điểm $B(0; 4)$ và $C(-1; 1)$
♦ Hàm số $y = – \dfrac{1}{2}x$:
Với $x = 2$ thì $y = -1$, ta được điểm $M(2; -1)$ thuộc đồ thị hàm số \(y = – \dfrac{1}{2}x\)
Vậy đồ thị hàm số \(y = – \dfrac{1}{2}x\) là đường thẳng đi qua hai điểm $O(0; 0)$ và điểm $M(2; -1)$
♦ Hàm số $y = – \dfrac{1}{2}x + 3x$:
Với $x = 0$ thì $y = 3$, ta được điểm $N(0; 3)$ thuộc đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\)
Với $y = 0$ thì $x = 6$ ta được điểm $P(6; 0)$ thuộc đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\)
Vậy đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\) là đường thẳng đi qua hai điểm $N(0; 3)$ và $P(6; 0)$
⇒ Ta vẽ đồ thị các hàm số \(y = 3{\rm{x}};y = 3{\rm{x}} + 4;y = – \dfrac{1}{2}x;y = – \dfrac{1}{2}x + 3\) trên cùng một mặt phẳng tọa độ như sau:

Giải bài 4 trang 77 Toán 8 tập 1 CD
Xác định đường thẳng \(y = ax + b \left( {a \ne 0} \right)\) có hệ số góc bằng $-1$ và đi qua điểm $M (1; 2)$. Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Bài giải:
Theo đề bài, đường thẳng $y = ax + b (a ≠ 0)$ có hệ số góc bằng $– 1$ nên đường thẳng có dạng $y = – x + b$.
Mặt khác, đường thẳng đi qua điểm $M(1; 2)$ nên ta có:
$– 1 + b = 2$ suy ra $b = 3$.
Do đó, đường thẳng cần tìm là $y = – x + 3$.
• Với $x = 0$ thì $y = – 0 + 3 = 0 + 3 = 3$, ta được điểm $A(0; 3)$ thuộc đồ thị của hàm số $y = – x + 3$.
• Với $y = 0$ thì $– x + 3 = 0$ suy ra $x = 3$, ta được điểm $B(3; 0)$ thuộc đồ thị của hàm số $y = – x + 3$.
Do đó, đồ thị của hàm số $y = – x + 3$ là đường thẳng đi qua hai điểm $A(0; 3)$ và $B(3; 0)$.
Ta vẽ đồ thị hàm số như sau:

Giải bài 5 trang 77 Toán 8 tập 1 CD
a) Vẽ đường thẳng $y = 2x -1$ trên mặt phẳng tọa độ.
b) Xác định đường thẳng \(y = ax + b \left( {a \ne 0} \right)\) đi qua điểm $M (1; 3)$ và song song với đường thẳng $y = 2x -1$. Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Bài giải:
a) Vẽ đường thẳng $y = 2x -1$ trên mặt phẳng tọa độ
Với $x = 0$ thì $y = -1$, ta được điểm $A(0; -1)$ thuộc đồ thị hàm số $y = 2x – 1$
Với $x = 1$ thì $y = 1$, ta được điểm $B(1; 1)$ thuộc đường thẳng $y = 2x – 1$
Đồ thị hàm số $y = 2x – 1$ là một đường thẳng đi qua hai điểm $A(0; -1)$ và điểm $B(1; 1)$
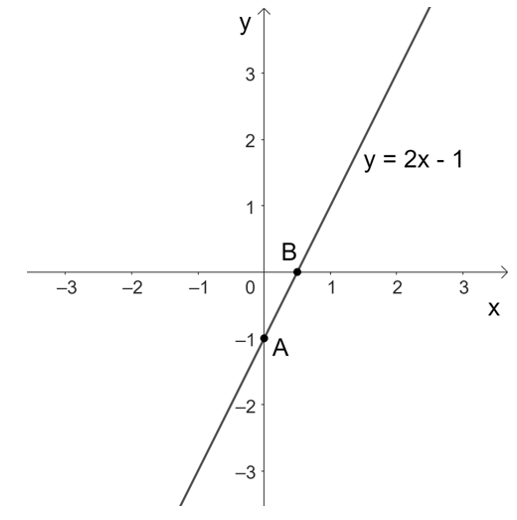
b) Vì đường thẳng \(y = ax + b \left( {a \ne 0} \right)\) song song với đường thẳng $y = 2x -1$ nên $a = 2$
Đường thẳng dã cho là: $y = 2x + b$
Vì đường thẳng $y = 2x + b$ đi qua điểm $M(1; 3)$ nên:
$3 = 2.1 + b$ suy ra $b = 1$
Vậy đường thẳng cần tìm là: $y = 2x + 1$
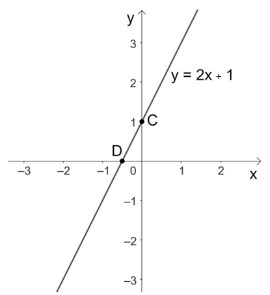
Vẽ đường thẳng $y = 2x + 1$:
Với $x = 0$ thì $y = 1$, ta được điểm $C(0, 1)$ thuộc đồ thị hàm số $y = 2x + 1$
Với $y = 0$ thì $x = – \dfrac{1}{2}$, ta được điểm $D(- \dfrac{1}{2}; 0)$ thuộc đồ thị hàm số $y = 2x + 1$
Đồ thị hàm số $y = 2x + 1$ là đường thẳng đi qua hai điểm $C(0, 1)$ và $D(- \dfrac{1}{2}; 0)$.
Giải bài 6 trang 77 Toán 8 tập 1 CD
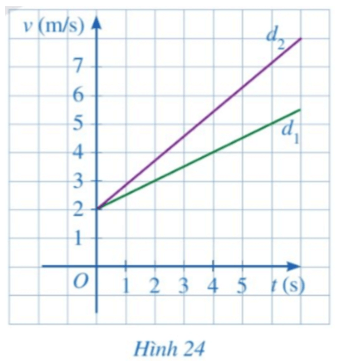
Một phần đường thẳng \({d_1},{d_2}\) ở Hình 24 lần lượt biểu thị tốc độ (đơn vị: m/s) của vật thứ nhất, vật thứ hai theo thời gian t (s).
a) Nêu nhận xét về tung độ giao điểm của hai đường thẳng \({d_1},{d_2}\). Từ đó, nêu nhận xét về tốc độ của hai chuyển động.
b) Trong hai đường thẳng \({d_1},{d_2}\), đường thẳng nào có hệ số góc lớn hơn?
c) Từ giây thứ nhất trở đi, vật nào có tốc độ lớn hơn? Vì sao?
Bài giải:
Quan sát Hình 24, ta thấy:
a) Tung độ giao điểm của hai đường thẳng \({d_1},{d_2}\) đều bằng $2$.
Nhận xét: Hai chuyển động đều có cùng tốc độ bạn đầu là $2m/s$.
b) Trong 2 đường thẳng \({d_1},{d_2}\) đường thẳng $d_2$ có hệ số góc lớn hơn.
c) Từ giây thứ nhất trở đi, vật thứ hai có tốc độ lớn hơn vì đường thẳng $d_2$ cao hơn đường thẳng $d_1$ từ giây thứ nhất.
Bài trước:
👉 Giải bài 1 2 3 4 5 6 trang 70 sgk Toán 8 tập 1 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 7 8 trang 78 79 sgk Toán 8 tập 1 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 trang 77 sgk Toán 8 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
