Nội Dung
Hướng dẫn giải Bài tập cuối chương VI sgk Toán 8 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 trang 37 38 sgk Toán 8 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
GIẢI BÀI TẬP CUỐI CHƯƠNG VI
Sau đây là phần Giải bài 1 2 3 4 5 trang 37 38 sgk Toán 8 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 37 Toán 8 tập 2 CD
Để học tốt môn Ngữ văn lớp 8, bạn Thảo đọc những văn bản truyện sau: Tôi đi học (Thanh Tịnh); Gió lạnh đầu mùa (Thạch Lam); Lão Hạc (Nam Cao); Người thầy đầu tiên (Chingiz Aitmatov); Tắt đèn (Ngô Tất Tố); Don Quixote (Miguel de Cervantes); Lá cờ thêu sáu chữ vàng (Nguyễn Huy Tưởng); Cái kính (Aziz Nesin).
Hãy phân nhóm những văn bản truyện nêu trên theo những tiêu chí sau:
| Truyện ngắn | Tên văn bản truyện, tác giả (liệt kê cụ thể) |
| Tiểu thuyết | Tên văn bản truyện, tác giả (liệt kê cụ thể) |
| Truyện lịch sử | Tên văn bản truyện, tác giả (liệt kê cụ thể) |
| Truyện cười | Tên văn bản truyện, tác giả (liệt kê cụ thể) |
Bài giải:
Ta phân nhóm những văn bản truyện nêu trên như sau:
| Truyện ngắn | Tôi đi học (Thanh Tịnh); Gió lạnh đầu mùa (Thạch Lam); Lão Hạc (Nam Cao); Người thầy đầu tiên (Chingiz Aitmatov) |
| Tiểu thuyết | Tắt đèn (Ngô Tất Tố); Don Quixote (Miguel de Cervantes) |
| Truyện lịch sử | Lá cờ thêu sáu chữ vàng (Nguyễn Huy Tưởng) |
| Truyện cười | Cái kính (Aziz Nesin) |
Giải bài 2 trang 37 Toán 8 tập 2 CD
Biểu đồ cột kép trong Hình 39 biểu diễn số lượng học sinh trung học cơ sở (THCS) và trung học phổ thông (THPT) của Việt Nam trong các năm học 2016 – 2017; 2017 – 2018, 2018 – 2019, 2019 – 2020.
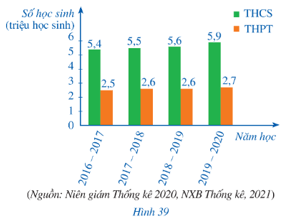
a) Lập bảng thống kê số lượng học sinh THCS và THPT của Việt Nam trong các năm học đó (đơn vị: triệu học sinh) theo mẫu sau:
| Năm học | 2016 – 2017 | 2017 – 2018 | 2018 – 2019 | 2019 – 2020 |
| Số học sinh THCS (triệu học sinh) | ? | ? | ? | ? |
| Số học sinh THPT (triệu học sinh) | ? | ? | ? | ? |
b) Lập bảng thống kê tỉ số giữa số lượng học sinh THCS và số lượng học sinh THPT của Việt Nam trong các năm học đó theo mẫu sau (viết tỉ số ở dạng số thập phân và làm tròn đến hàng phần mười):
| Năm học | 2016 – 2017 | 2017 – 2018 | 2018 – 2019 | 2019 – 2020 |
| Tỉ số của số học sinh THCS và số học sinh THPT | ? | ? | ? | ? |
c) Nêu nhận xét về sự thay đổi của các tỉ số trong Bảng 12.
Bài giải:
a) Từ biểu đồ cột kép ở Hình 39, ta có bảng thống kê số lượng học sinh THCS và THPT của Việt Nam trong các năm học đó như sau:
| Năm học | 2016 – 2017 | 2017 – 2018 | 2018 – 2019 | 2019 – 2020 |
| Số học sinh THCS (triệu học sinh) | 5,4 | 5,5 | 5,6 | 5,9 |
| Số học sinh THPT (triệu học sinh) | 2,5 | 2,6 | 2,6 | 2,7 |
b) Ta có:
– Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2016 – 2017 là: \(\frac{5,4}{2,5} \approx 2,2\).
– Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2017 – 2018 là: \(\frac{5,5}{2,6} \approx 2,1\).
– Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2018 – 2019 là: \(\frac{5,6}{2,6} \approx 2,2\).
– Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2019 – 2020 là: \(\frac{5,9}{2,7} \approx 2,2\).
Ta có bảng thống kê tỉ số giữa số lượng học sinh THCS và số lượng học sinh THPT của Việt Nam trong các năm học đó như sau:
| Năm học | 2016 – 2017 | 2017 – 2018 | 2018 – 2019 | 2019 – 2020 |
| Tỉ số của số học sinh THCS và số học sinh THPT | 2,2 | 2,1 | 2,2 | 2,2 |
c) Trong Bảng 12, ta thấy rằng tỉ số của số học sinh THCS và số học sinh THPT qua các năm học gần như là không thay đổi. Điều này cho thấy số lượng học sinh tham gia học THCS và THPT trong các năm khá ổn định, không có quá nhiều sự biến đổi.
Giải bài 3 trang 38 Toán 8 tập 2 CD
Biểu đồ đoạn thẳng trong Hình 40 biểu diễn tuổi thọ trung bình của người Việt Nam qua 30 năm (từ năm 1989 đến năm 2019).
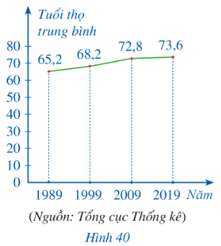
a) Lập bảng thống kê tuổi thọ trung bình của người Việt Nam trong các năm đó theo mẫu sau (đơn vị: tuổi):
| Năm | 1989 | 1999 | 2009 | 2019 |
| Tuổi thọ trung bình | ? | ? | ? | ? |
b) Một bài báo có nêu thông tin: So với năm 1989, tuổi thọ trung bình của người Việt Nam trong năm 2019 đã tăng lên $14\%$. Thông tin của bài báo đó có chính xác không?
Bài giải:
a) Từ biểu đồ đoạn thẳng ở Hình 40, ta có bảng thống kê tuổi thọ trung bình của người Việt Nam trong các năm 1989, 1999, 2009, 2019 (đơn vị: tuổi) như sau:
| Năm | 1989 | 1999 | 2009 | 2019 |
| Tuổi thọ trung bình | 65,2 | 68,2 | 72,8 | 73,6 |
b) Tỉ số phần trăm giữa tuổi thọ trung bình của người Việt Năm năm 2019 so với năm 1989 là:
\(\frac{73,6.100}{65,2}\% \approx 113\%\)
Tuổi thọ trung bình của người Việt Năm năm 2019 so với năm 1989 đã tăng số $\%$ là:
\(113\% – 100\% = 13\% \)
Vậy thông tin của bài báo là không chính xác.
Giải bài 4 trang 38 Toán 8 tập 2 CD
Trong trò chơi vòng quay số đã giới thiệu ở Hoạt động 2 của §4, tính xác suất của biến cố:
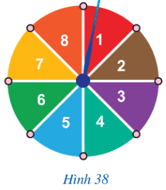
a) “Chiếc kim chỉ vào hình quạt ghi số chia cho $4$ dư $3$”;
b) “Chiếc kim chỉ vào hình quạt ghi số chỉ có đúng một ước nguyên tố”.
Bài giải:
a) Có $8$ kết quả có thể xảy ra là: $1; 2; 3; 4; 5; 6; 7; 8$.
Có $2$ kết quả thuận lợi của biến cố “Chiếc kim chỉ vào hình quạt ghi số chia cho $4$ dư $3$” là: $3; 7$.
Xác suất của biến cố “Chiếc kim chỉ vào hình quạt ghi số chia cho $4$ dư $3$” là: \(\frac{2}{8} = \frac{1}{4}\).
b) Có $6$ kết quả thuận lợi của biến cố “Chiếc kim chỉ vào hình quạt ghi số chỉ có đúng một ước nguyên tố” là: $2; 3; 4; 5; 7; 8$.
Xác suất của biến cố “Chiếc kim chỉ vào hình quạt ghi số chỉ có đúng một ước nguyên tố” là: \(\frac{6}{8} = \frac{3}{4}\).
Giải bài 5 trang 38 Toán 8 tập 2 CD
Một hộp có $5$ chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số nguyên dương không vượt quá $5$, hai thẻ khác nhau thì ghi hai số khác nhau. Lấy ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp.
a) Sau $40$ lần lấy thẻ liên tiếp, hãy tính xác suất thực nghiệm của các biến cố sau “Thẻ lấy ra ghi số chẵn” và “Thẻ lấy ra ghi số lẻ”.
b) Tính xác suất của các biến cố “Thẻ lấy ra ghi số chẵn” và “Thẻ lấy ra ghi số lẻ”.
c) Nêu mối liên hệ giữa xác suất thực nghiệm của mỗi biến cố “Thẻ lấy ra ghi số chẵn” và “Thẻ lấy ra ghi số lẻ” với xác suất của mỗi biến cố đó khi số lần lấy thẻ ngày càng lớn.
Bài giải:
a) Vì lấy thẻ $40$ lần liên tiếp nên xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số chẵn” ngày càng gần xác suất của biến cố đó.
Vì lấy thẻ $40$ lần liên tiếp nên xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số lẻ” ngày càng gần xác suất của biến cố đó.
b) Số kết quả có thể xảy ra khi rút thẻ là: $5$.
Có $2$ kết quả thuận lợi của biến cố “Thẻ lấy ra ghi số chẵn” là: $2, 4$.
Xác suất của biến cố “Thẻ lấy ra ghi số chẵn” là \(\frac{2}{5}\).
Có $3$ kết quả thuận lợi của biến cố “Thẻ lấy ra ghi số lẻ” là: $1, 3, 5$.
Xác suất của biến cố “Thẻ lấy ra ghi số chẵn” là \(\frac{3}{5}\).
c) Khi số lần lấy thẻ càng lớn thì xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số chẵn” ngày càng gần với xác suất của nó là \(\frac{2}{5}\).
Khi số lần lấy thẻ càng lớn thì xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số lẻ” ngày càng gần với xác suất của nó là \(\frac{3}{5}\).
Hoặc:
Tập hợp gồm các kết quả có thể xảy ra đối với số ghi trên thẻ khi lấy ngẫu nhiên một chiếc thẻ trong hộp là:
$B = \{1; 2; 3; 4; 5\}$.
Tập hợp $B$ có $5$ phần tử.
a) Ghi lại số của thẻ lấy ra sau $40$ lần rút thẻ liên tiếp, ta được kết quả như sau:
| Số ghi trên thẻ | 1 | 2 | 3 | 4 | 5 |
| Số lần xuất hiện | 9 | 5 | 6 | 8 | 12 |
Chú ý: Kết quả được ghi lại ở trên là ngẫu nhiên.
⦁ Xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số chẵn” là: \(\frac{5 + 8}{40} = \frac{13}{40}\).
⦁ Xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số lẻ” là:\(1 – \frac{13}{40} = \frac{27}{40}\).
Bài trước:
👉 Giải bài 1 2 3 4 trang 36 sgk Toán 8 tập 2 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 7 8 trang 43 44 sgk Toán 8 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 trang 37 38 sgk Toán 8 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
