Nội Dung
Hướng dẫn giải Bài §28. Hàm số bậc nhất và đồ thị của hàm số bậc nhất sgk Toán 8 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 24 25 26 27 28 29 trang 50 sgk Toán 8 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
Bài 28 HÀM SỐ BẬC NHẤT VÀ ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT
Bài toán mở đầu trang 47 Toán 8 tập 2 KNTT
Một ô tô đi từ bến xe Giáp Bát (Hà Nội) đến thành phố Vinh (Nghệ An) Với vận tốc $60$ km/h. Hỏi sau $t$ giờ ô tô đó cách trung tâm Hà Nội bao nhiêu kilômét? Biết rằng bến xe Giáp Bát cách trung tâm Hà Nội $7$ km và coi rằng trung tâm Hà Nội, bến xe Giáp Bát và thành phố Vinh nằm trên cùng một đường thẳng.

Trả lời:
Quãng đường đi được của ô tô sau $t$ giờ là $60t$ (km).
Khoảng cách từ vị trí của ô tô đến trung tâm Hà Nội sau $t$ giờ là $60t + 7$ (km).
1. KHÁI NIỆM HÀM SỐ BẬC NHẤT
Hoạt động 1 trang 47 Toán 8 tập 2 KNTT
Xét bài toán mở đầu.
Viết công thức tính quãng đường $S$ đi được của ô tô sau $t$ giờ. Quãng đường $s$ có phải là một hàm số của thời gian không?
Trả lời:
Công thức tính quãng đường $S$ đi được của ô tô sau $t$ giờ $S=60t$ (km).
Quãng đường $S$ là một hàm số của thời gian $t$.
Hoạt động 2 trang 47 Toán 8 tập 2 KNTT
Viết công thức tính khoảng cách $d$ từ vị trí của ô tô đến trung tâm Hà Nội sau $t$ giờ.
Trả lời:
Công thức tính khoảng cách d từ vị trí của ô tô đến trung tâm Hà Nội sau $t$ giờ là: $d = 60t + 7$ (km).
Hoạt động 3 trang 47 Toán 8 tập 2 KNTT
Từ kết quả của HĐ2, hãy hoàn thành bảng sau vào vở.
| $t$ (giờ) | $1$ | $2$ | $3$ | $4$ | $5$ |
| $d (km)$ | $?$ | $?$ | $?$ | $?$ | $?$ |
Khoảng cách $d$ có phải là một hàm số của thời gian $t$ không?
Trả lời:
Với $t = 1$ thì $d = 60 . 1 + 7 = 67$;
Với $t = 2$ thì $d = 60 . 2 + 7 = 127$;
Với $t = 3$ thì $d = 60 . 3 + 7 = 187$;
Với $t = 4$ thì $d = 60 . 4 + 7 = 247$;
Với $t = 5$ thì $d = 60 . 5 + 7 = 307$;
Vậy ta hoành thành được bảng như sau:
| $t$ (giờ) | $1$ | $2$ | $3$ | $4$ | $5$ |
| $d (km)$ | $67$ | $127$ | $187$ | $247$ | $307$ |
Câu hỏi trang 48 Toán 8 tập 2 KNTT
Trong các hàm số sau, những hàm số nào là hàm số bậc nhất?
a) $y = 3x – 2$;
b) $y = -2x$;
c) \(y = 2x^2 + 3\);
d) $y = 3(x – 1)$;
e) $y = 0x + 1$.
Trả lời:
a) $y = 3x – 2$ là hàm số bậc nhất.
b) $y = -2x$ là hàm số bậc nhất.
c) \(y = 2x^2 + 3\) không phải là hàm số bậc nhất vì bậc của $x$ trong hàm số \(y = 2x^2 + 3\) là $2$.
d) $y = 3(x – 1) = 3x – 3$ là hàm số bậc nhất.
e) $y = 0x + 1$ không phải là hàm số bậc nhất vì $a = 0$.
Vận dụng trang 48 Toán 8 tập 2 KNTT
Trong hệ đo lường Mỹ, quãng đường thường được đo bằng dặm (mile) và $1$ dặm bằng khoảng $1,609 km$.
a) Viết công thức để chuyển đổi $x$ (dặm) sang $y (km)$. Công thức tính $y$ theo $x$ này có phải là một hàm số bậc nhất của $x$ không?
b) Một ô tô chạy với vận tốc $55$ dặm/giờ trên một quãng đường có quy định vận tốc tối đa là $80$ km/h. Hỏi ô tô đó có vi phạm luật giao thông không?
Trả lời:
a) Vì $1$ dặm bằng khoảng $1,609 km$ nên $x$ dặm bằng khoảng $1,609x \,km$.
Do đó, công thức chuyển đổi $x$ (dặm) sang $y (km)$ là: $y = 1,609x$.
Công thức tính $y$ theo $x$ là một hàm số bậc nhất của $x$.
b) Vận tốc của ô tô tính bằng km/h là:
$1,609 . 55 = 88,495 \,km/h > 80 km/h$.
Vậy ô tô đã vi phạm luật giao thông.
Tranh luận trang 48 Toán 8 tập 2 KNTT
Pi: Hàm số \(y = \frac{{x + 1}}{2}\) có phải là hàm số bậc nhất không?
Vuông: Đây là hàm số bậc nhất.
Tròn: Không đúng, tớ nghĩ đây không phải hàm số bậc nhất.
Theo em, Vuông hay Tròn ai nói đúng? Vì sao?
Trả lời:
Ta có:
\(y = \frac{{x + 1}}{2} = \frac{x}{2} + \frac{1}{2} = \frac{1}{2}x + \frac{1}{2}\)
Vậy hàm số \(y = \frac{{x + 1}}{2}\) là hàm số bậc nhất.
Như thế, thì Vuông nói đúng.
2. ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT
Hoạt động 4 trang 48 Toán 8 tập 2 KNTT
Cho hàm số bậc nhất $y=2x−1$.
Hoàn thành bảng giá trị sau vào vở:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=2x−1$ | $?$ | $?$ | $?$ | $?$ | $?$ |
Trả lời:
Ta có:
Với $x = – 2$ thì $y = 2 . (– 2) – 1 = – 5$;
Với $x = – 1$ thì $y = 2 . (– 1) – 1 = – 3$;
Với $x = 0$ thì $y = 2 . 0 – 1 = – 1$;
Với $x = 1$ thì $y = 2 . 1 – 1 = 1$;
Với $x = 2$ thì $y = 2 . 2 – 1 = 3$;
Vậy ta hoàn thành được bảng như sau:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=2x−1$ | $5$ | $-3$ | $-1$ | $1$ | $3$ |
Hoạt động 5 trang 49 Toán 8 tập 2 KNTT
Gọi $A, B, C, D, E$ là các điểm trên đồ thị hàm số $y=2x−1$ có hoành độ $x$ lần lượt là $-2; -1; 0; 1; 2$. Từ kết quả của HĐ4, hãy xác định tọa độ các điểm $A, B, C, D, E$.
Trả lời:
Với $x = -2$ ta có: $y = 2.(-2) – 1= -5$, suy ra $A(-2; -5)$
Với $x= -1$ ta có $y = 2.(-1) -1 = -3$, suy ra $B(-1; -3)$
Với $x = 0$ ta có $y = 2. 0 -1 = -1$, suy ra $C(0; -1)$
Với $x = 1$ ta có $y = 2. 1 – 1 = 1$, suy ra $D(1; 1)$
Với $x = 2$ ta có $y = 2. 2 – 1 = 3$, suy ra $E(2; 3)$
Hoạt động 6 trang 49 Toán 8 tập 2 KNTT
Trên mặt phẳng tọa độ $Oxy$, biểu diễn các điểm $A, B, C, D, E$ trong HĐ5. Dùng thước thẳng để kiểm nghiệm rằng các điểm này cùng nằm trên một đường thẳng.
Trả lời:
Ta biểu diễn các điểm $A, B, C, D, E$ trên cùng một mặt phẳng tọa độ như sau:
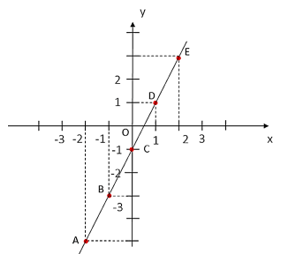
Dùng thước thẳng ta thấy các điểm $A, B, C, D, E$ cùng nằm trên một đường thẳng.
Luyện tập trang 49 Toán 8 tập 2 KNTT
Vẽ đồ thị của các hàm số $y=−2x+3$ và \(y = \frac{1}{2}x\).
Trả lời:
♦ Xét hàm số $y = –2x + 3$
Cho $x = 0$ thì $y = 3$, ta được giao điểm của đồ thị hàm số $y = –2x + 3$ với trục $Oy$ là $A(0; 3)$.
Cho $x = 1$ thì $y = 1$, ta được điểm $B(1; 1)$ thuộc đồ thị hàm số $y = –2x + 3$.
⇒ Đồ thị hàm số $y = –2x + 3$ là đường thẳng $AB$.
♦ Xét hàm số \(y = \frac{1}{2}x\)
Cho $x = 0$ thì $y = 0$, ta được điểm ở gốc tọa độ $O(0; 0)$ thuộc đồ thị hàm số \(y = \frac{1}{2}x\).
Cho $x = 2$ thì $y = 1$, ta được điểm $C(2; 1)$ thuộc đồ thị hàm số \(y = \frac{1}{2}x\).
⇒ Đồ thị hàm số \(y = \frac{1}{2}x\) là đường thẳng $OC$.
Ta vẽ đồ thị như sau

GIẢI BÀI TẬP
Sau đây là phần Giải bài 24 25 26 27 28 29 trang 50 sgk Toán 8 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 7.24 trang 50 Toán 8 tập 2 KNTT
Trong các hàm số sau, những hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số $a, b$ của chúng.
a) $y=0.x−5$;
b) $y=1−3x$;
c) $y=−0,6x$;
d) $y= \sqrt 2(x−1)+3$;
e) \(y = 2x^2 + 1\).
Bài giải:
a) $y=0.x−5$ không là hàm số bậc nhất do hệ số của $x$ là $0$.
b) $y=1−3x$ là hàm số bậc nhất với $a = –3; b = 1$.
c) $y=−0,6x$ là hàm số bậc nhất với $a=−0,6, b=0$.
d) $y= \sqrt 2(x−1)+3$ là hàm số bậc nhất với $a= \sqrt 2, b = – \sqrt 2 + 3$.
e) \(y = 2x^2 + 1\) không phải là hàm số bậc nhất vì bậc của $x$ ở đây là $2$.
Giải bài 7.25 trang 50 Toán 8 tập 2 KNTT
Cho hàm số bậc nhất $y=ax+3$.
a) Tìm hệ số $a$, biết rằng khi $x=1$ thì $y=5$.
b) Với giá trị $a$ tìm đượcc, hãy hoàn thành bảng giá trị sau vào vở:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y$ | $?$ | $?$ | $?$ | $?$ | $?$ |
Bài giải:
a) Thay $x = 1, y = 5$ vào công thức hàm số $y = ax + 3$ ta được:
$5 = a.1 + 3$, suy ra $a = 2$.
Vậy $y = 2x + 3$.
b) Ta có:
Với $x = – 2$ thì $y = 2 . (– 2) + 3 = – 1$;
Với $x = – 1$ thì $y = 2 . (– 1) + 3 = 1$;
Với $x = 0$ thì $y = 2 . 0 + 3 = 3$;
Với $x = 1$ thì $y = 2 . 1 + 3 = 5$;
Với $x = 2$ thì $y = 2 . 2 + 3 = 7$;
Vậy ta hoàn thành được bảng như sau:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y$ | $-1$ | $1$ | $3$ | $5$ | $7$ |
Giải bài 7.26 trang 50 Toán 8 tập 2 KNTT
Vẽ đồ thị của các hàm số sau:
a) $y=2x−6$;
b) $y=−3x+5$;
c) \(y = \frac{3}{2}x\).
Bài giải:
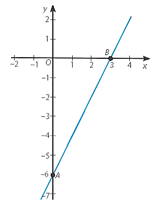
a) Vẽ đồ thị hàm số $y = 2x – 6$
Cho $x = 0$ thì $y = – 6$, ta được giao điểm của đồ thị với trục $Oy$ là $A(0; – 6)$.
Cho $y = 0$ thì $x = 3$, ta được giao điểm của đồ thị với trục $Ox$ là $B(3; 0)$.
⇒ Đồ thị của hàm số $y = 2x – 6$ là đường thẳng $AB$.
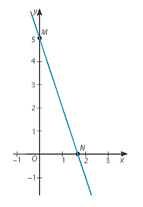
b) Vẽ đồ thị hàm số $y = –3x + 5$
Cho $x = 0$ thì $y = 5$, ta được giao điểm của đồ thị với trục $Oy$ là $M(0; 5)$.
Cho $y = 0$ thì $x = \frac{5}{3}$, ta được giao điểm của đồ thị với trục $Ox$ là $N(\frac{5}{3}; 0)$.
Đồ thị của hàm số $y = –3x + 5$ là đường thẳng $MN$.
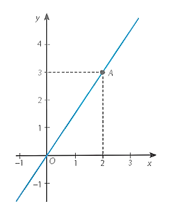
c) Vẽ đồ thị hàm số \(y = \frac{3}{2}x\)
Cho $x = 0$ thì $y = 0$, ta có đồ thị hàm số đi qua gốc tọa độ $O(0; 0)$.
Cho $x = 2$ thì $y = 3$, ta có đồ thị hàm số đi qua điểm $A(2; 3)$.
Đồ thị của hàm số \(y = \frac{3}{2}x\) là đường thẳng $OA$.
Giải bài 7.27 trang 50 Toán 8 tập 2 KNTT
Đồng euro (EUR) là đơn vị tiền tệ chính thức ở một số quốc gia thành viên của Liên minh châu Âu. Vào một ngày, tỉ giá hối đoái giữa đồng euro và đồng đô là Mỹ (USD) là: $1$ EUR = $1,1052$ USD.
a) Viết công thức để chuyển đổi $x$ euro sang $y$ đô la Mỹ. Công thức tính $y$ theo $x$ này có phải là một hàm số bậc nhất của $x$ không?
b) Vào ngày đó, $200$ euro có giá trị bằng khoảng bao nhiêu đô la Mỹ?
c) Vào ngày đó, $500$ đô la Mỹ có giá trị bằng khoảng bao nhiêu euro?
(Làm tròn kết quả của câu b và câu c đến hàng đơn vị).
Bài giải:
a) Vì $1$ EUR = $1,1052$ USD nên $x$ EUR = $1,1052x$ USD.
Do đó công thức để chuyển đổi $x$ euro sang $y$ đô la Mỹ là $y = 1,1052x$.
Công thức tính $y$ theo $x$ này là một hàm số bậc nhất của $x$ với $a = 1,1052$ và $b = 0$.
b) Thay $x = 200$ vào công thức $y = 1,1052x$, ta có:
$y = 1,1052 . 200 ≈ 221$.
Vậy vào ngày đó, $200$ euro có giá trị bằng khoảng $221$ đô la Mỹ.
c) Thay $y = 500$ vào công thức $y = 1,1052x$, ta có:
$500 = 1,1052x$ hay $x = \frac{500}{1,1052} ≈ 452$
Vậy vào ngày đó, $500$ đô là Mỹ có giá trị bằng khoảng $452$ euro.
Giải bài 7.28 trang 50 Toán 8 tập 2 KNTT
Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là $22 \,000$ đồng/tháng và cước gọi là $800$ đồng/ phút
a) Lập công thức tính số điện cước điện thoại $y$ (đồng) phải trả trong tháng khi gọi $x$ phút.
b) Tính số tiền cước điện thoại phải trả khi gọi $75$ phút.
c) Nếu số tiền cước điện thoại phải trả là $94 000$ đồng thì trong tháng đó thuê bao đã gọi bao nhiêu phút?
Bài giải:
a) Công thức tính số điện cước điện thoại $y$ (đồng) phải trả trong tháng khi gọi $x$ phút là:
$y = 800x + 22 \,000$ (đồng).
b) Số tiền cước điện thoại phải trả khi gọi $75$ phút, tức là $x = 75$ là:
$y = 800 . 75 + 22 \,000 = 82 000$ (đồng).
c) Nếu số tiền cước điện thoại phải trả là $94 000$ đồng, tức $y = 94 \,000$, thay giá trị này vào công thức $y = 800x + 22 \,000$, ta được:
$94 \,000 = 800x + 22 \,000$, suy ra $x = 90$.
Vậy trong tháng đó thuê bao đã gọi $90$ phút.
Giải bài 7.29 trang 50 Toán 8 tập 2 KNTT
Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất $y=ax+b$, trong đó $b$ biểu thị chi phí cố định của hoạt động kinh doanh và hệ số $a$ biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là $36$ triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là $1,8$ triệu đồng.
a) Viết công thức của hàm số bậc nhất biểu thị chi phí $y$ (triệu đồng) để sản xuất $x$ (xe đạp) trong một ngày.
b) Vẽ đồ thị hàm số thu được ở câu a.
c) Chi phí để sản xuất $15$ chiếc xe đạp trong một ngày là bao nhiêu?
d) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là $72$ triệu đồng?
Bài giải:
a) Chi phí cố định hằng ngày là $36$ triệu đồng nên $b = 36$.
Chi phí sản xuất mỗi chiếc xe đạp là $1,8$ triệu đồng nên $a = 1,8$.
Do đó, công thức của hàm số bậc nhất biểu thị chi phí $y$ (triệu đồng) để sản xuất $x$ (xe đạp) trong một ngày là:
$y = 1,8x + 36$.
b) Cho $x = 0$ thì $y = 36$ ta được giao điểm của đồ thị hàm số với trục $Oy$ là $M(0; 36)$.
Cho $y = 0$ thì $x = –20$, ta được giao điểm của đồ thị hàm số với trục $Ox$ là $N(–20; 0)$.
Đồ thị của hàm số $y = 1,8x + 36$ là đường thẳng $MN$.

c) Chi phí để sản xuất $15$ chiếc xe đạp (tức $x = 15$) trong $1$ ngày là:
$y = 1,8 . 15 + 36 = 63$ (triệu đồng).
d) Thay $y = 72$ vào công thức hàm số $y = 1,8x + 36$ ta được:
$72 = 1,8x + 36$
Suy ra $x = 20$ (chiếc xe).
Vậy với chi phí trong ngày là $72$ triệu đồng thì có thể sản xuất được $20$ chiếc xe đạp.
Bài trước:
👉 Giải bài 18 19 20 21 22 23 trang 44 45 46 sgk Toán 8 tập 2 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 30 31 32 33 34 35 trang 54 sgk Toán 8 tập 2 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 24 25 26 27 28 29 trang 50 sgk Toán 8 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
