Nội Dung
Hướng dẫn giải Bài §14. Hình thoi và hình vuông sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 29 30 31 32 33 trang 71 72 sgk Toán 8 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
Bài 14 HÌNH THOI VÀ HÌNH VUÔNG
Bài toán mở đầu trang 67 Toán 8 tập 1 KNTT
Lấy một tờ giấy, gấp làm tư tạo ra một góc vuông $O$, đánh dấu hai điểm $A, B$ trên hai cạnh góc vuông rồi cắt chéotheo đoạn thẳng $AB$ (H.3.46a). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác đó là hình gì? Vì sao? Nếu ta có $OA = OB$ thì tứ giác nhận được là hình gì (H.3.46b)?
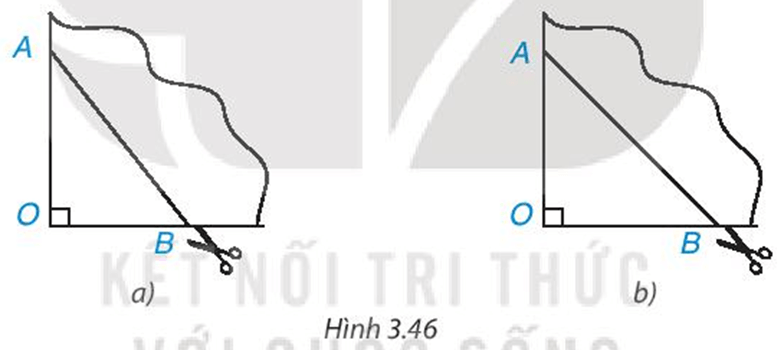
Trả lời:
♦ Hình 3.46a):
Khi gấp làm tư tạo ra một góc vuông $O$, đánh dấu hai điểm $A, B$ trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh $AB$.
Khi đó, tứ giác $ABCD$ là hình thoi.
♦ Hình 3.46b):
Khi gấp làm tư tạo ra một góc vuông $O$, đánh dấu hai điểm $A, B$ trên hai cạnh góc vuông. Nếu $OA = OB$ thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.
1. HÌNH THOI
Câu hỏi trang 67 Toán 8 tập 1 KNTT
Hình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi.
Trả lời:
Hình thoi có bốn cạnh bằng nhau nên ta suy ra hai cặp cạnh đối bằng nhau. Do đó hình thoi cũng là hình bình hành.
Ta suy ra tính chất hình thoi dựa vào tính chất của hình bình hành như sau:
– Hình thoi có hai góc đối bằng nhau.
– Hình thoi có các cặp cạnh đối song song.
– Hình thoi có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Hoạt động 1 trang 68 Toán 8 tập 1 KNTT
Cho hình thoi $ABCD$ có hai đường chéo $AC, BD$ cắt nhau tại $O$ (H.3.48).
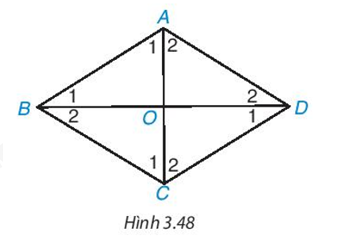
a) $∆ABD$ có cân tại $A$ không?
b) $AC$ có vuông góc với $BD$ không và $AC$ có là đường phân giác của góc $A$ không? Vì sao?
Trả lời:
a) Vì tứ giác $ABCD$ là hình thoi nên $AB = AD$.
Suy ra $∆ABD$ có cân tại $A$.
b) Vì tứ giác $ABCD$ là hình thoi nên $AB = BC = CD = DA$.
Xét $∆ABC$ và $∆ADC$ có:
$AB = AD$ (chứng minh trên);
$BC = CD$ (chứng minh trên);
Cạnh $AC$ chung.
Do đó $∆ABC = ∆ADC$ (c.c.c)
Suy ra \(\)\(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng)
Hay $AC$ là đường phân giác của góc $A$.
Tam giác $ABD$ cân tại $A$ có $AO$ là đường phân giác của góc $A$ (vì $AC$ là đường phân giác góc $A$) nên $AO$ cũng là đường cao.
Khi đó $AO ⊥ BD$ hay $AC ⊥ BD$.
Vậy $AC$ vuông góc với $BD$ và $AC$ là đường phân giác của góc $A$.
Câu hỏi trang 68 Toán 8 tập 1 KNTT
Hãy viết giả thiết, kết luận của câu c trong Định lí 2.
Trả lời:
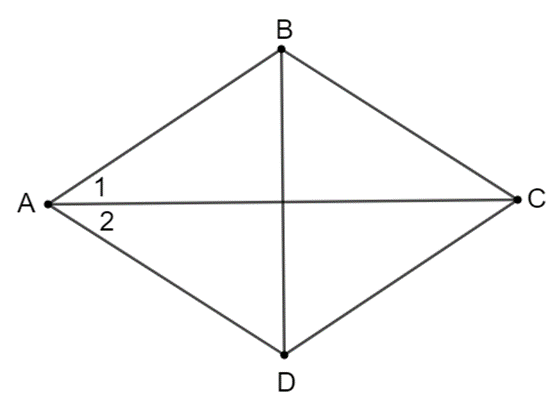
Giả thiết, kết luận của Định lí 2.
a) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
| GT | Hình bình hành $ABCD$ có $AB = BC$. |
| KL | $ABCD$ là hình thoi. |
Ta có thể viết giả thiết đối với các cặp cạnh kề khác, chẳng hạn như:
Hình bình hành $ABCD$ có $BC = CD$ hoặc $CD = DA$ hoặc $DA = AB$.
b) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
| GT | Hình bình hành $ABCD$ có $AC ⊥ BD$. |
| KL | $ABCD$ là hình thoi. |
c) Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
| GT | Hình bình hành $ABCD$ có \(\widehat {A_1} = \widehat {A_2}\). |
| KL | $ABCD$ là hình thoi. |
Ta có thể viết giả thiết tương tự đối với tia phân giác góc $B$ hoặc góc $C$ hoặc góc $D$.
Luyện tập 1 trang 69 Toán 8 tập 1 KNTT
Trong Hình 3.51, hình nào là hình thoi? Vì sao?

Trả lời:
♦ Hình 3.51a):
Tứ giác đã cho có hai đường chéo cắt nhau tại trung điểm của mỗi đường và chúng vuông góc với nhau nên tứ giác đó là hình thoi.
♦ Hình 3.51b):
Gọi tứ giác trong Hình 3.51b) là tứ giác $ABCD$.
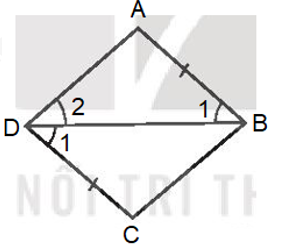
Vì \(\widehat {{B_1}} = \widehat {{D_1}}\) mà hai góc này ở vị trí so le trong nên $AB // CD$.
Mà $AB = CD$ nên tứ giác $ABCD$ là hình bình hành.
Mặt khác, \(\widehat {{D_1}} = \widehat {{D_2}}\) hay $DB$ là tia phân giác của \(\widehat {ADC}\)
Khi đó, hình bình hành $ABCD$ có $DB$ là tia phân giác của \(\widehat {ADC}\).
Do đó tứ giác $ABCD$ là hình thoi.
♦ Hình 3.51c):
Tứ giác trong Hình 3.51c) hai đường chéo vuông góc với nhau và có đường chéo là đường vuông góc của một góc của tứ giác.
Từ đó ta suy ra tứ giác đã cho không phải là hình thoi.
Vậy Hình 3.51a và Hình 3.51b là hình thoi.
2. HÌNH VUÔNG
Hoạt động 2 trang 70 Toán 8 tập 1 KNTT
Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
Trả lời:
Hình vuông cũng là hình thoi, hình chữ nhật.
Mà hình chữ nhật có hai đường chéo bằng nhau còn hình thoi có hai đường chéo vuông góc với nhau.
Do đó, hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
Câu hỏi trang 70 Toán 8 tập 1 KNTT
Hãy viết giả thiết, kết luận của câu a trong Định lí 4.
Trả lời:
Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
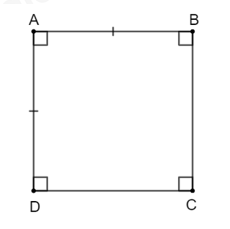
| GT | Hình chữ nhật $ABCD$ có $AB = AD$. |
| KL | $ABCD$ là hình vuông. |
Ta có thể viết giả thiết đối với cặp cạnh kề khác như: $AB = BC; \,BC = CD; \,CD = AD$.
Luyện tập 2 trang 71 Toán 8 tập 1 KNTT
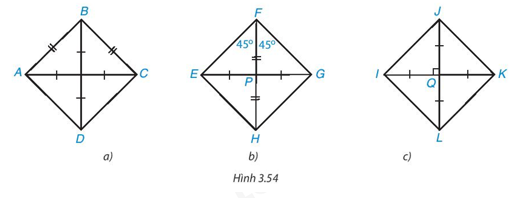
Với mỗi hình dưới đây, ta dùng dấu hiệu nhận biết nào để khẳng định đó là hình vuông?
Trả lời:
♦ Hình 3.54a):
Tứ giác $ABCD$ có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra tứ giác này là hình chữ nhật.
Mà $AB = BC$ nên tứ giác $ABCD$ là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
♦ Hình 3.54b):
Tứ giác $EFGH$ có hai đường chéo cắt nhau tại trung điểm $P$ của mỗi đường.
Ta có $\widehat {EFG} = \widehat {EFP} + \widehat {GFP} = {45^o} + {45^o} = {90^o}$
Suy ra tứ giác $EFGH$ là hình chữ nhật.
Hình chữ nhật $EFGH$ có đường chéo $FH$ là đường phân giác của \(\widehat {EFG}\).
Do đó tứ giác $EFGH$ là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có một đường chéo là đường phân giác của một góc của hình vuông.
♦ Hình 3.54c):
Tứ giác $IJKL$ có hai đường chéo $IK$ và $JL$ bằng nhau và cắt nhau tại trung điểm $Q$ của mỗi đường.
Suy ra tứ giác $IJKL$ là hình chữ nhật.
Mà $IK ⊥ JL$ nên tứ giác $IJKL$ là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai đường chéo vuông góc là hình vuông.
Vận dụng trang 71 Toán 8 tập 1 KNTT
Trở lại tình huống mở đầu. Hãy giải thích tại sao:
– Trong trường hợp a, ta được hình thoi.
– Trong trường hợp b, ta được hình vuông.
Trả lời:
– Trong trường hợp a):
Khi gấp làm tư tạo ra một góc vuông $O$, đánh dấu hai điểm $A, B$ trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh $AB$.
Khi đó, tứ giác $ABCD$ là hình thoi.
– Trong trường hợp b):
Khi gấp làm tư tạo ra một góc vuông $O$, đánh dấu hai điểm $A, B$ trên hai cạnh góc vuông. Nếu $OA = OB$ thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 29 30 31 32 33 trang 71 72 sgk Toán 8 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 3.29 trang 71 Toán 8 tập 1 KNTT
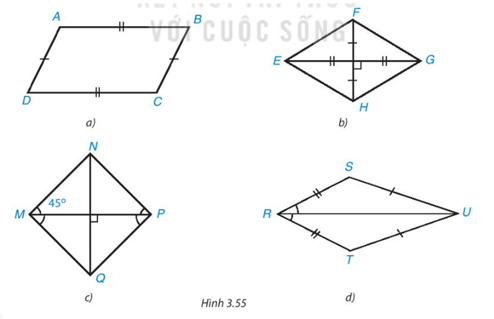
Tìm các hình thoi và hình vuông trong Hình 3.55.
Bài giải:
♦ Xét Hình 3.55a):
Tứ giác $ABCD$ có $AB = CD; \,AD = BC$.
Suy ra tứ giác $ABCD$ là hình bình hành.
♦ Xét Hình 3.55b):
Tứ giác $EFGH$ có hai đường chéo $EG$ và $FH$ cắt nhau tại trung điểm của mỗi đường. Suy ra tứ giác $EFGH$ là hình bình hành.
Hình bình hành $EFGH$ có hai đường chéo vuông góc với nhau. Do đó tứ giác $EFGH$ là hình thoi.
♦ Xét Hình 3.55c):
Tam giác $MNP$ có:
$\widehat {NMP} = \widehat {NPM} = {45^0}$
$⇒ \widehat {MNP} = {180^0} – {45^0} – {45^0} = {90^0}\) (1)
$\widehat {NMP} = {45^0} + {45^0} = {90^0}$ (2)
$\widehat {NPQ} = {45^0} + {45^0} = {90^0}$ (3)
Từ (1), (2) và (3) suy ra $MNPQ$ là hình chữ nhật (vì có 3 góc vuông).
Xét hình chữ nhật $MNPQ$ có \(MP \bot NQ\) nên $MNPQ$ là hình vuông (dựa theo dấu hiệu nhận biết hình vuông).
♦ Xét Hình 3.55d):
Tứ giác $SRTU$ là hình cái diều (không phải hình thoi) vì các cạnh của tứ giác không bằng nhau.
Giải bài 3.30 trang 72 Toán 8 tập 1 KNTT
Cho tam giác $ABC$, $D$ là một điểm nằm giữa $B$ và $C$. Qua $D$ kẻ các đường thẳng song song với $AB, AC$, chúng cắt các cạnh $AC, AB$ lần lượt tại $E, F$.
a) Tứ giác $AEDF$ là hình gì? Vì sao?
b) Nếu tam giác $ABC$ cân tại $A$ thì điểm $D$ ở vị trí nào trên cạnh $BC$ để tứ giác $AEDF$ là hình thoi?
c) Nếu tam giác $ABC$ vuông tại $A$ thì tứ giác $AEDF$ là hình gì?
d) Nếu tam giác $ABC$ vuông cân tại $A$ thì điểm $D$ ở vị trí nào trên cạnh $BC$ để $AEDF$ là hình vuông?
Bài giải:
Ta có hình vẽ minh họa sau:
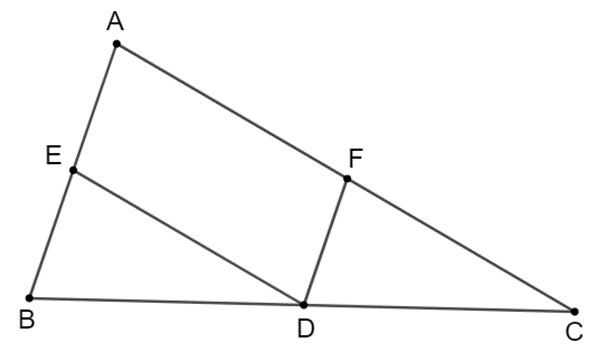
a) Tứ giác $AEDF$ có $AE // DF; \,AF // DE$ (giả thiết).
Suy ra tứ giác $AEDF$ là hình bình hành.
b) Hình bình hành $AEDF$ là hình thoi khi $AD$ là tia phân giác của góc $A$
Mà tam giác $ABC$ cân tại $A$ nên đường phân giác $AD$ đồng thời là đường trung tuyến.
Do đó $D$ là trung điểm của $BC$.
Ngược lại, nếu $D$ là trung điểm của cạnh $BC$ của tam giác $ABC$ cân tại $A$ thì hình bình hành $AEDF$ có đường chéo $AD$ là đường phân giác của góc $A$ nên $AEDF$ là hình thoi.
c) Nếu $ΔABC$ vuông tại $A$ thì tứ giác $AEDF$ là hình chữ nhật (vì hình vuông là hình bình hành có một góc vuông).
d) Tam giác $ABC$ vuông cân tại $A$ tức là vừa vuông tại $A$ vừa cân tại $A$.
Theo câu c, nếu $ΔABC$ vuông tại $A$ thì $AEDF$ là hình chữ nhật.
Để hình chữ nhật $AEDF$ là hình vuông thì tức nó cũng là hình thoi.
Theo câu b, $AEDF$ là hình thoi nếu $D$ là trung điểm của cạnh $BC$ của tam giác $ABC$ cân tại $A$.
Vậy nếu tam giác $ABC$ vuông cân tại $A$ thì để $AEDF$ là hình vuông thì điểm $D$ là trung điểm của $BC$.
Giải bài 3.31 trang 72 Toán 8 tập 1 KNTT
Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.
Bài giải:
Giả sử có hình chữ nhật $ABCD$. Gọi $E, F, G, H$ lần lượt là trung điểm của $AB, BC, CD, DA$. Ta có hình vẽ minh họa sau:
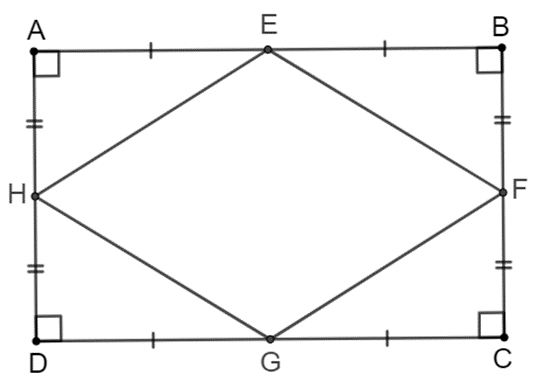
Xét các tam giác $AEH, BEF, CGF, DGH$ có:
\( \widehat A = \widehat B = \widehat C = \widehat D = 90^0\)
$AE = BE = CG = DG$ (vì $E, G$ là trung điểm của $AB, CD$ và $AB = CD$)
$EH = EF = GF = GH$ (vì $F, H$ là trung điểm của $BC, AD$ và $BC = AD$)
\(⇒ \Delta AEH = \Delta BEF = \Delta CGF = \Delta DGH \)
Suy ra $EH = EF = FG = GH$ (các cạnh tương ứng) nên tứ giác $EFGH$ là hình thoi (vì có 4 cạnh bằng nhau).
Giải bài 3.32 trang 72 Toán 8 tập 1 KNTT
Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.
Bài giải:
Giả sử có hình thoi $ABCD$. Gọi $E, F, G, H$ lần lượt là trung điểm của $AB, BC, CD, DA$. Ta có hình vẽ minh họa sau:

Ta cần chứng minh $EFGH$ là hình chữ nhật. Thật vậy:
Do $ABCD$ là hình thoi nên:
$AB = BC = CD = DA$
Do $E, H$ lần lượt là trung điểm của $AB, AD$ nên:
$AH = DH = AE = BE$
Tam giác $AHE$ có $AH = AE$ nên là tam giác cân tại $A$, suy ra \(\widehat {AHE} = \widehat {AEH}\)
Mà \(\widehat {HAE} + \widehat {AHE} + \widehat {AEH} = 180^\circ \)
Suy ra \(\widehat {AHE} = \frac{{180^\circ – \widehat {HAE}}}{2}\)
Tương tự, ta có tam giác $DHG$ cân tại $D$ nên:
\(\widehat {DHG} = \frac{{180^\circ – \widehat {HDG}}}{2}\)
Mặt khác, do $ABCD$ là hình thoi nên $AB // CD$
Suy ra \(\widehat {HAE} + \widehat {HDG} = 180^\circ \)
Khi đó:
\(\widehat {AHE} + \widehat {DHG} = \frac{{180^\circ – \widehat {HAE}}}{2} + \frac{{180^\circ – \widehat {HDG}}}{2}\)
\(= \frac{{180^\circ – \widehat {HAE} + 180^\circ – \widehat {HDG}}}{2}\)
\(= \frac{{360^\circ – (\widehat {HAE} + \widehat {HDG})}}{2}\)
\(= \frac{{360^\circ – 180^\circ }}{2}\)
Mà \(\widehat {AHE} + \widehat {DHG} + \widehat {EHG} = 180^\circ \)
Suy ra \(\widehat {EHG} = 180^\circ – (\widehat {AHE} + \widehat {DHG}) = 180^\circ – 90^\circ = 90^\circ \)
Chứng minh tương tự như trên ta cũng có \(\widehat {HEF} = \widehat {EFG} = \widehat {FGH} = {90^0}.\)
Tứ giác $EFGH$ có bốn góc vuông nên là hình chữ nhật.
Giải bài 3.33 trang 72 Toán 8 tập 1 KNTT
Cho hình chữ nhật $ABCD$ có chu vi bằng $36 cm$. Gọi $M$ là trung điểm của cạnh $BC$. Biết rằng $MA ⊥ MD$. Tính độ dài các cạnh của hình chữ nhật $ABCD$ (H.3.56).
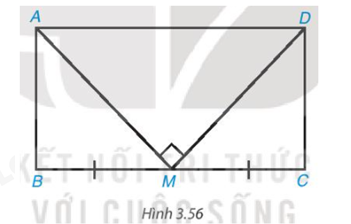
Bài giải:
Gọi $I$ là trung điểm của $AD$.

Theo tính chất của đường trung tuyến ứng với cạnh huyền, ta có:
\(MI = \frac{{A{\rm{D}}}}{2}\) (1)
Xét tứ giác $ABMI$ có:
\( \widehat A = \widehat B = \widehat I = 90^0 \Leftrightarrow ABMI\) là hình chữ nhật.
$⇒ AB = MI$ (2)
Từ (1) và (2) suy ra \(AB = \frac{{A{\rm{D}}}}{2}\) nên $AD = 2AB$.
Mà \(AB + A{\rm{D}} = \frac{{36}}{2} = 18\) (cm).
Suy ra $AB + 2AB = 18$
Hay $3AB = 18$
Do đó $AB = 6 (cm)$.
Suy ra $AD = 2AB = 2 . 6 = 12 (cm)$.
Vậy độ dài các cạnh của hình chữ nhật $ABCD$ là $AB = CD = 6 cm; \,AD = BC = 12 cm$.
Bài trước:
👉 Giải bài 25 26 27 28 trang 66 sgk Toán 8 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 34 35 36 37 38 trang 73 sgk Toán 8 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 29 30 31 32 33 trang 71 72 sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
