Nội Dung
Hướng dẫn giải Bài 28. Phép chia đa thức một biến sgk Toán 7 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 30 31 32 33 34 35 trang 43 sgk Toán 7 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
BÀI 28. PHÉP CHIA ĐA THỨC MỘT BIẾN
Bài toán mở đầu trang 39 Toán 7 tập 2 KNTT
Tìm đa thức $P$ sao cho $A = B. P$, trong đó $A = 2x^4 – 3x^3 – 3x^2 + 6x – 2$ và $B = x^2 – 2$.
Tròn: “Mình nghĩ mãi là chưa giải được bài toán này. Vuông có cách nào giải không?”
Vuông: “Ừ nhỉ! Nếu A và B là hai số thì chỉ việc lấy A chia cho B là xong nhưng A và B lại là hai đa thức”.
Pi: “Cũng thế thôi các em ạ. Trước hết các em phải tìm hiểu cách chia hai đa thức”.
Trả lời:
Ta thực hiện theo các bước sau:
Bước 1. Lấy hạng tử có bậc cao nhất của A chia cho hạng tử có bậc cao nhất của B:
$2x^4 : x^2 = 2x^2$.
Bước 2. Lấy A trừ đi tích $B. 2x^2$ ta được dư thứ nhất là $-3x^3 + x^2 + 6x – 2$.
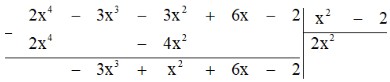
Bước 3. Lấy hạng tử cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B:
$(-3x^3) : x^2 = -3x$.
Bước 4. Lấy dư thứ nhất trừ đi tích $B. (-3x)$ ta được dư thứ hai là $x^2 – 2$.
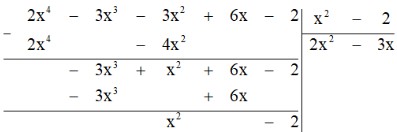
Bước 5. Lấy hạng tử cao nhất của dư thứ hai chia cho hạng tử bậc cao nhất của B:
$x^2 : x^2 = 1$.
Bước 6. Lấy dư thứ nhất trừ đi tích $B. 1$ ta được dư thứ ba là $0$.
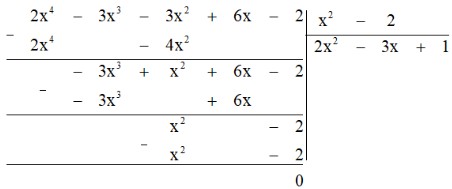
Bước 7. Dư cuối cùng bằng 0 nên quá trình chia kết thúc.
Vậy $A : B = 2x^2 – 3x + 1$.
1. LÀM QUEN VỚI PHÉP CHIA ĐA THỨC
Hoạt động 1 trang 40 Toán 7 tập 2 KNTT
Tìm thương của mỗi phép chia sau:
a) $12x^3 : 4x$;
b) $(2x^4 ) : x^4$;
c) $2x^5 : 5x^2$.
Trả lời:
a) Ta có:
$12x^3 : 4x = (12:4) . (x^3 : x) = 3.x^2$
b) Ta có:
$(-2x^4 ) : x^4 = [(-2) : 1] . (x^4 : x^4) = -2$
c) Ta có:
$2x^5 : 5x^2 = (2:5) . (x^5 : x^2) = \frac{2}{5}x^3$
Hoạt động 2 trang 40 Toán 7 tập 2 KNTT
Giả sử $x \ne 0$. Hãy cho biết:
a) Với điều kiện nào (của hai số mũ) thì thương hai lũy thừa của x cũng là một lũy thừa của x với số mũ nguyên dương?
b) Thương hai lũy thừa của $x$ cùng bậc bằng bao nhiêu?
Trả lời:
a) Do \({x^m}:{x^n} = {x^{m – n}}\) nên muốn thương hai lũy thừa của $x$ cũng là một lũy thừa của $x$ với số mũ nguyên dương, tức là $m – n > 0$ thì $m > n$.
b) Ta có:
\({x^m}:{x^m} = {x^{m – m}} = {x^0} = 1\)
Vậy thương hai lũy thừa của $x$ cùng bậc bằng $1$.
Luyện tập 1 trang 40 Toán 7 tập 2 KNTT
Thực hiện các phép chia sau:
a) $3{x^7}:\frac{1}{2}{x^4}$;
b) $(- 2x):x$;
c) $0,25{x^5}:( – 5{x^2})$.
Trả lời:
a) Ta có:
$3{x^7}:\dfrac{1}{2}{x^4} = (3:\dfrac{1}{2}).({x^7}:{x^4}) = 6{x^3}$
b) Ta có:
$(- 2x):x = [( – 2):1].(x:x) = – 2$
c) Ta có:
$0,25{x^5}:( – 5{x^2}) = [0,25:( – 5)].({x^5}:{x^2}) = – 0,05.{x^3}$
2. CHIA ĐA THỨC CHO ĐA THỨC, TRƯỜNG HỢP CHIA HẾT
Câu hỏi trang 41 Toán 7 tập 2 KNTT
Kiểm tra lại rằng ta có phép chia hết $A : B = 2x^2 – 5x + 1$, nghĩa là xảy ra:
$A = B . (2x^2 – 5x + 1)$.
Trả lời:
Ta có:
$B . (2x^2 – 5x + 1)$
$= (x^2 – 4x – 3) . (2x^2 – 5x + 1)$
$= x^2 .(2x^2 – 5x + 1) – 4x . (2x^2 – 5x + 1) – 3.(2x^2 – 5x + 1)$
$= x^2 . 2x^2 + x^2 . (-5x) + x^2 . 1 – [4x . 2x^2 + 4x . (-5x) + 4x . 1] \\– [3.2x^2 + 3.(-5x) + 3.1]$
$= 2x^4 – 5x^3 + x^2 – ( 8x^3 – 20x^2 + 4x) – (6x^2 – 15x + 3)$
$= 2x^4 – 5x^3 + x^2 – 8x^3 + 20x^2 – 4x – 6x^2 + 15x – 3$
$= 2x^4 + (-5x^3 – 8x^3) + (x^2 + 20x^2 – 6x^2 ) + (-4x + 15x) – 3$
$= 2x^4 – 13x^3 + 15x^2 + 11x – 3$
$= A$
Vậy ta có phép chia hết $A : B = 2x^2 – 5x + 1$
Luyện tập 2 trang 41 Toán 7 tập 2 KNTT
Thực hiện phép chia:
a) $(-x^6 + 5x^4 – 2x^3) : (0,5x^2)$;
b) $(9x^2 – 4) : (3x + 2)$.
Trả lời:
a) Ta có:
$(-x^6 + 5x^4 – 2x^3) : (0,5x^2)$
$= (-x^6 : 0,5x^2) + (5x^4 : 0,5x^2) + (-2x^3 : 0,5x^2)$
$= -2x^4 + 10x^2 – 4x$
Vậy $(-x^6 + 5x^4 – 2x^3) : (0,5x^2) = -2x^4 + 10x^2 – 4x$.
b) Ta có:
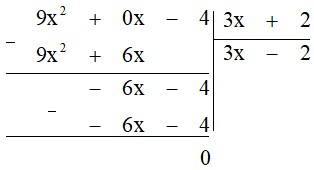
Vậy $(9x^2 – 4) : (3x + 2) = 3x – 2$.
Vận dụng trang 41 Toán 7 tập 2 KNTT
Em hãy giải bài toán trong tình huống mở đầu.
Trả lời:
Ta có: $A = B . P$ nên $P = A : B$
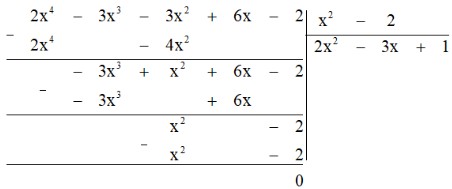
3. CHIA ĐA THỨC CHO ĐA THỨC, TRƯỜNG HỢP CHIA CÓ DƯ
Hoạt động 3 trang 42 Toán 7 tập 2 KNTT
Hãy mô tả lại các bước đã thực hiện trong phép chia đa thức D cho đa thức E.
Trả lời:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của D chia cho hạng tử bậc cao nhất của E.
Bước 2: Lấy D trừ đi tích của E với thương mới thu được ở bước 1.
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của E.
Bước 4: Lấy dư thứ nhất trừ đi tích E với thương vừa thu được ở bước 3. Ta được dư thứ hai có bậc nhỏ hơn bậc của E thì quá trình chia kết thúc.
Hoạt động 4 trang 42 Toán 7 tập 2 KNTT
Kí hiệu dư thứ hai là $G = – 6x + 10$. Đa thức này có bậc bằng $1$. Lúc này phép chia có thể tiếp tục được không? Vì sao?
Trả lời:
Lúc này phép chia không thực hiện được nữa vì bậc của đa thức $-6x + 10$ (là $1$) nhỏ hơn bậc của đa thức chia $x^2 + 1$ (là $2$).
Hoạt động 5 trang 42 Toán 7 tập 2 KNTT
Hãy kiểm tra lại đẳng thức $D = E . (5x – 3) + G$.
Trả lời:
Ta có:
$E . (5x – 3) + G$
$= (x^2 + 1) . (5x – 3) + (-6x + 10)$
$= x^2 .(5x – 3) + 1. (5x – 3) + (-6x) + 10$
$= x^2 . 5x + x^2 . (-3) + 5x – 3 – 6x + 10$
$= 5x^3 – 3x^2 + (5x – 6x) + (-3 + 10)$
$= 5x^3 – 3x^2 – x + 7$
$= D$
Vậy đẳng thức đúng.
Luyện tập 3 trang 42 Toán 7 tập 2 KNTT
Tìm dư $R$ và thương $Q$ trong phép chia đa thức $A= 3x^4 – 6x – 5$ cho đa thức $B = x^2 + 3x – 1$ rồi viết $A$ dưới dạng $A = B . Q + R$.
Trả lời:
Thực hiện phép chia ta được:
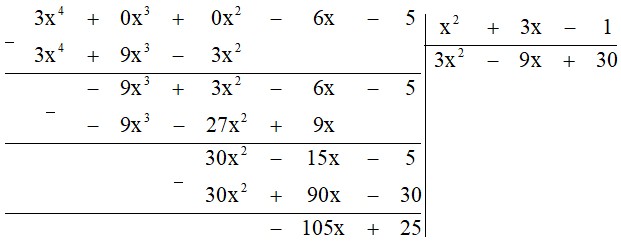
Do đó dư $R$ bằng $-105x + 25$; thương $Q$ bằng $3x^2 – 9x + 30$.
Vậy $A = (x^2 + 3x – 1) . (3x^2 – 9x + 30) -105x + 25$.
Thử thách nhỏ trang 42 Toán 7 tập 2 KNTT
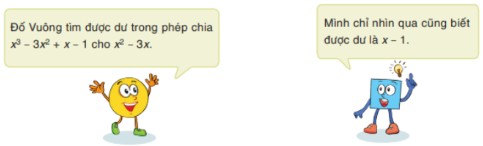
Em có biết tại sao Vuông làm nhanh thế không?
Trả lời:
Ta có:
$x^3 – 3x^2 + x – 1 = (x^3 – 3x^2 ) + (x -1)$.
Vì $x^3 – 3x^2$ chia cho $x^2 – 3x$ không dư; bậc của $x – 1$ nhỏ hơn bậc của $x^2 – 3x$ nên số dư của phép chia $(x^3 – 3x^2 ) + (x -1)$ cho $x^2 – 3x$ là $x – 1$.
Vậy Vuông làm nhanh và đúng.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 30 31 32 33 34 35 trang 43 sgk Toán 7 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 7.30 trang 43 Toán 7 tập 2 KNTT
Tính:
a) $8x^5 : 4x^3$;
b) $120x^7 : (-24x^5)$;
c) $\dfrac{3}{4}{( – x)^3}:\dfrac{1}{8}x$;
d) $-3,72x^4 : (-4x^2)$.
Bài giải:
a) Ta có:
$8x^5 : 4x^3 = (8 : 4) . (x^5 : x^3) = 2.x^2$
b) Ta có:
$120x^7 : (-24x^5) = [120 : (-24)] . (x^7 : x^5) = -5.x^2$
c) Ta có:
$\dfrac{3}{4}{( – x)^3}:\dfrac{1}{8}x = \dfrac{{ – 3}}{4}{x^3}:\dfrac{1}{8}x = \left( {\dfrac{{ – 3}}{4}:\dfrac{1}{8}} \right).({x^3}:x) = – 6{x^2}$
d) Ta có:
$-3,72x^4 : (-4x^2) = [(-3,72) : (-4)] . (x^4 : x^2) = 0,93x^2$
Giải bài 7.31 trang 43 Toán 7 tập 2 KNTT
Thực hiện các phép chia đa thức sau:
a) $(-5x^3 + 15x^2 + 18x) : (-5x)$;
b) $(-2x^5 – 4x^3 + 3x^2) : 2x^2$.
Bài giải:
a) Ta có:
$(-5x^3 + 15x^2 + 18x) : (-5x)$
$= (-5x^3) : (-5x) + 15x^2 : (-5x) + 18x : (-5x)$
$= [(-5): (-5)] . (x^3 : x) + [15 : (-5)] . (x^2 : x) + [18 : (-5)]. (x : x)$
$= x^2 – 3x – \dfrac{{18}}{5}$.
b) Ta có:
$(-2x^5 – 4x^3 + 3x^2) : 2x^2$
$= (-2x^5 : 2x^2) + (-4x^3 : 2x^2) + (3x^2 : 2x^2)$
$= [(-2) : 2] . (x^5 : x^2) + [(-4) : 2] . (x^3 : x^2) + (3 : 2) . (x^2 : x^2)$
$= -x^3 – 2x + \dfrac{3}{2}$.
Giải bài 7.32 trang 43 Toán 7 tập 2 KNTT
Thực hiện phép chia đa thức sau bằng cách đặt tính chia:
a) $(6x^3 – 2x^2 – 9x + 3) : (3x – 1)$;
b) $(4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)$.
Bài giải:
a) Thực hiện đặt phép chia ta được:
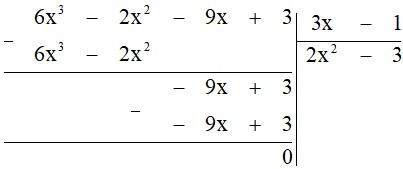
b) Thực hiện đặt phép chia ta được:
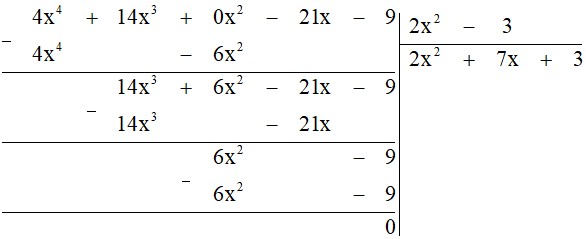
Giải bài 7.33 trang 43 Toán 7 tập 2 KNTT
Thực hiện phép chia $0,5x^5 + 3,2x^3 – 2x^2$ cho $0,25x^n$ trong mỗi trường hợp sau:
a) $n = 2$.
b) $n = 3$.
Bài giải:
a) Ta có:
$(0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^2$
$= 0,5x^5 : 0,25x^2 + 3,2x^3 : 0,25x^2 + (2x^2 : 0,25x^2)$
$= (0,5:0,25).(x^5 : x^2) + (3,2 : 0,25). (x^3 : x^2 ) + (2 : 0,25). (x^2 : x^2)$
$= 2x^3 + 12,8x + 4$
b) Ta có:
$(0,5x^5 + 3,2x^3 – 2x^2 ) : 0,25x^3$
Thực hiện đặt phép chia ta được:
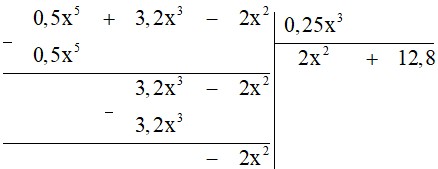
Giải bài 7.34 trang 43 Toán 7 tập 2 KNTT
Trong mỗi trường hợp sau đây, tìm thương $Q(x)$ và dư $R(x)$ trong phép chia $F(x)$ cho $G(x)$ rồi biểu diễn $F(x)$ dưới dạng:
$F(x) = G(x) . Q(x) + R(x)$.
a) $F(x) = 6x^4 – 3x^3 + 15x^2 + 2x – 1$; $G(x) = 3x^2$;
b) $F(x) = 12x^4 + 10x^3 – x – 3$; $G(x) = 3x^2 + x + 1$.
Bài giải:
a) Ta có:
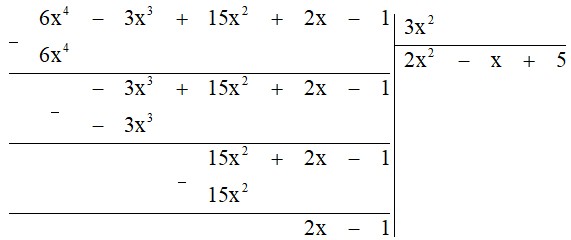
Thương $Q(x) = 2x^2 – x + 5$
Dư $R(x) = 2x – 1$
Vậy:
$F(x) = 3x^2 . (2x^2 – x + 5) + 2x – 1$
b) Ta có:
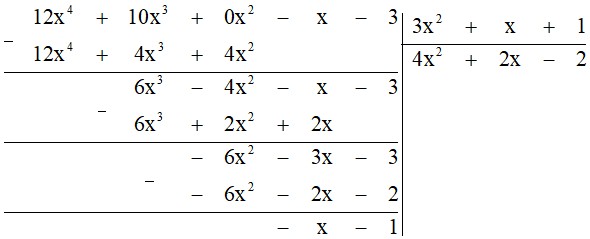
Thương $Q(x) = 4x^2 + 2x – 2$
Dư $R(x) = -x – 1$
Vậy:
$F(x) = (3x^2 + x + 1) . (4x^2 + 2x – 2) – x – 1$
Giải bài 7.35 trang 43 Toán 7 tập 2 KNTT
Bạn Tâm lúng túng khi muốn tìm thương và dư trong phép chia đa thức $21x – 4$ cho $3x^2$. Em có thể giúp bạn Tâm được không?
Bài giải:
Chia đa thức $21x – 4$ cho $3x^2$ được thương là $0$, dư $21x – 4$.
Bài trước:
👉 Giải bài 23 24 25 26 27 28 29 trang 38 sgk Toán 7 tập 2 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 36 37 38 39 40 41 trang 45 sgk Toán 7 tập 2 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 30 31 32 33 34 35 trang 43 sgk Toán 7 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
