Nội Dung
Hướng dẫn giải Bài Luyện tập chung trang 83 sgk Toán 7 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 31 32 33 34 35 trang 83 sgk Toán 7 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
GIẢI BÀI TẬP LUYỆN TẬP CHUNG
Sau đây là phần Giải bài 31 32 33 34 35 trang 83 sgk Toán 7 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 9.31 trang 83 Toán 7 tập 2 KNTT
Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.
Bài giải:
Ta vẽ hình minh họa như sau:
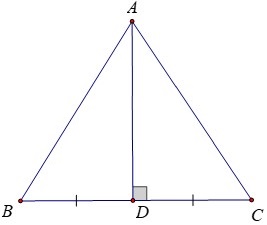
Từ $A$ kẻ đường thẳng $m$ vuông góc với $BC$ tại trung điểm $D$ của $BC$.
\(\Rightarrow AD\) là đường trung tuyến của $BC$.
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
$\widehat {ADB} = \widehat {ADC} = {90^0}\\AD:chung\\BD = CD\left( {gt} \right)\\ \Rightarrow \Delta ABD = \Delta ACD\left( {c – g – c} \right)$
\(\Rightarrow AB = AC\) (2 cạnh tương ứng)
\(\Rightarrow \Delta ABC\) cân tại $A$ (đpcm).
Giải bài 9.32 trang 83 Toán 7 tập 2 KNTT
Cho ba điểm phân biệt thẳng hàng $A, B, C$. Gọi $d$ là đường thẳng vuông góc với $AB$ tại $A$. Với điểm $M$ thuộc $d$, $M$ khác $A$, vẽ đường thẳng $CM$. Qua $B$ kẻ đường thẳng vuông góc với đường thẳng $CM$, cắt $d$ tại $N$. Chứng minh đường thẳng $BM$ vuông góc với đường thẳng $CN$.
Bài giải:
Ta vẽ hình minh họa như sau:
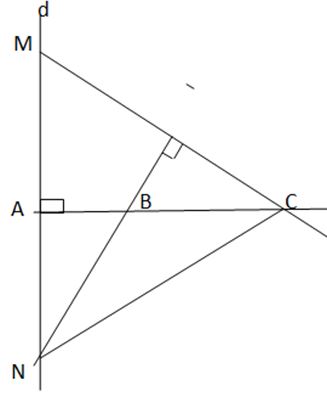
Xét tam giác $MNC$ có
• $BN \bot CM$
• $CA \bot MN$
• \(BN \cap CA =\) {B}
\( \Rightarrow B\) là trực tâm của tam giác $MNC$
\(\Rightarrow MB \bot CN\).
Giải bài 9.33 trang 83 Toán 7 tập 2 KNTT
Có một mảnh tôn hình tròn cần đục lỗ ở tâm. Làm thế nào để xác định được tâm của mảnh tôn đó?
Bài giải:
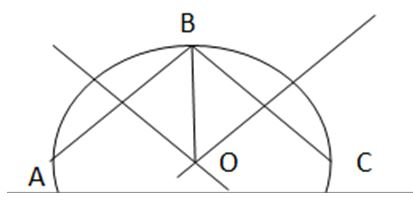
– Lấy ba điểm phân biệt $A, B, C$ trên đường viền ngoài mảnh tôn.
– Vẽ đường trung trực cạnh $AB$ và cạnh $BC$. Hai đường trung trực này cắt nhau tại $O$. Khi đó $O$ là tâm cần xác định.
Giải bài 9.34 trang 83 Toán 7 tập 2 KNTT
Cho tam giác $ABC$. Kẻ tia phân giác $At$ của góc tạo bởi tia $AB$ và tia đối của $AC$. Chứng minh rằng nếu đường thẳng chứa tia $At$ song song với đường thẳng $BC$ thì tam giác $ABC$ cân tại $A$.
Bài giải:
Gọi $AM$ là tia đối của $AC$.
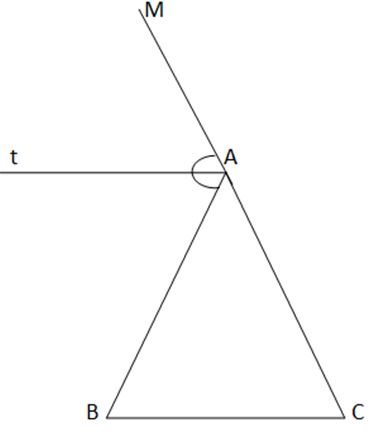
$At$ là đường phân giác của \(\widehat {MAB} \Rightarrow \widehat {MAt} = \widehat {BAt}\)
Ta có: \(At\parallel BC\) nên:
\(\widehat {ABC} = \widehat {BAt}\) (hai góc sole trong)
\(\widehat {ACB} = \widehat {MAt}\) (hai góc đồng vị)
Mà \(\widehat {MAt} = \widehat {BAt}\) \(\Rightarrow \widehat {ABC} = \widehat {ACB}\)
Vậy tam giác $ABC$ cân tại $A$ (dấu hiệu nhận biết tam giác cân).
Giải bài 9.35 trang 83 Toán 7 tập 2 KNTT
Kí hiệu \({S_{ABC}}\) là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC.
a) Chứng minh \({S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\).
Gợi ý: Sử dụng \(GM = \dfrac{1}{3}AM\) để chứng minh \({S_{GMB}} = \dfrac{1}{3}{S_{ABM}},{S_{GCM}} = \dfrac{1}{3}{S_{ACM}}\).
b) Chứng minh \({S_{GCA}} = {S_{GAB}} = \dfrac{1}{3}{S_{ABC}}\).
Nhận xét. Từ bài tập trên ta có: $S_{GBC} = S_{GCA} = S_{GAB} =\dfrac{1}{3}{S_{ABC}}$ điều này giúp ta cảm nhận tại sao có thể đặt thăng bằng miếng bìa hình tam giác trên giá nhọn đặt tại trọng tâm của tam giác đó.
Bài giải:
a) Vì G là trọng tâm tam giác ABC nên \(GM = \dfrac{1}{3}AM\)
Kẻ \(BP \bot AM\)
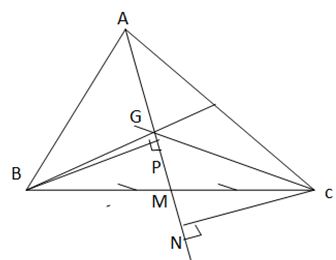
Ta có:
${S_{GMP}} = \dfrac{1}{2}BP.GM\\{S_{ABM}} = \dfrac{1}{2}BP.AM$
\(\Rightarrow \dfrac{{{S_{GMP}}}}{{{S_{ABM}}}} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \Rightarrow {S_{GMP}} = \dfrac{1}{3}{S_{ABM}}\)(1)
Tương tự, kẻ \(CN \bot AM\), ta có:
${S_{GMC}} = \dfrac{1}{2}CN.GM\\{S_{ACM}} = \dfrac{1}{2}CN.AM\\ \Rightarrow \dfrac{{{S_{GMC}}}}{{{S_{ACM}}}} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \Rightarrow {S_{GMC}} = \dfrac{1}{3}{S_{ACM}}\left( 2 \right)$
Cộng 2 vế của (1) và (2) ta có:
${S_{GMB}} + {S_{GMC}} = \dfrac{1}{3}\left( {{S_{AMC}} + {S_{ABM}}} \right)\\ \Rightarrow {S_{GBC}} = \dfrac{1}{3}{S_{ABC}}$
b) Ta có:
${S_{GAB}} = \dfrac{1}{2}BP.AG\\{S_{GAC}} = \dfrac{1}{2}CN.AG$
Xét \(\Delta BPM\) và \(\Delta CNM\) có:
\(\widehat {BPM} = \widehat {CNM} = {90^0}\)
$BM = CM$ ($M$ là trung điểm của $BC$)
\(\widehat {PMB} = \widehat {CMN}\) (2 góc đối đỉnh)
\(\Rightarrow \Delta BPM = \Delta CNM\) (cạnh huyền – góc nhọn)
\(\Rightarrow BP = CN\) (cạnh tương ứng)
\(\Rightarrow {S_{GAB}} = {S_{GAC}}\)
Ta có: \(AG = \dfrac{2}{3}AM\)
${S_{ACB}} = {S_{GAB}} + {S_{GAC}} + {S_{GCB}}\\ \Rightarrow {S_{ACB}} = {S_{GAB}} + {S_{GAC}} + \dfrac{1}{3}{S_{ABC}}\\ \Rightarrow \dfrac{2}{3}{S_{ABC}} = 2{S_{GAC}}\\ \Rightarrow \dfrac{1}{3}{S_{ABC}} = {S_{GAC}} = {S_{GAB}}$.
Vậy \({S_{GCA}} = {S_{GAB}} = \dfrac{1}{3}{S_{ABC}}\) (đpcm).
Bài trước:
👉 Giải bài 26 27 28 29 30 trang 81 sgk Toán 7 tập 2 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 36 37 38 39 40 trang 84 sgk Toán 7 tập 2 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 31 32 33 34 35 trang 83 sgk Toán 7 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
