Toán 7 – KNTT

Giải bài 36 37 38 39 40 41 trang 45 sgk Toán 7 tập 2 Kết Nối Tri Thức

Hướng dẫn giải Bài Luyện tập chung trang 45 sgk Toán 7 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 36 37 38 39 40 41 trang 45 sgk Toán 7 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.

GIẢI BÀI TẬP LUYỆN TẬP CHUNG

Sau đây là phần Giải bài 36 37 38 39 40 41 trang 45 sgk Toán 7 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 7.36 trang 45 Toán 7 tập 2 KNTT

Rút gọn biểu thức sau:

$(5x^3 – 4x^2) : 2x^2 + (3x^4 + 6x) : 3x – x(x^2 – 1)$.

Bài giải:

Ta có:

$(5x^3 – 4x^2) : 2x^2 + (3x^4 + 6x) : 3x – x(x^2 – 1)$

$= 5x^3 : 2x^2 + (-4x^2 : 2x^2) + 3x^4 : 3x + 6x : 3x – [x. x^2 + x . (-1)]$

$= (5:2) . (x^3 : x^2) + [(-4) : 2] . (x^2 : x^2) + (3 : 3) . (x^4 : x) + (6 : 3). (x:x) – (x^3 – x)$

$= \dfrac{5}{2} x – 2 + x^3 + 2 – x^3 + x$

$= (x^3 – x^3) + (\dfrac{5}{2} x + x) + (-2 + 2)$

$= 0 + \dfrac{7}{2} x + 0$

$= \dfrac{7}{2} x$

Giải bài 7.37 trang 45 Toán 7 tập 2 KNTT

Rút gọn các biểu thức sau:

a) $2x(x+3) – 3x^2(x+2) + x(3x^2 + 4x – 6)$;

b) $3x(2x^2 – x) – 2x^2(3x+1) + 5(x^2 – 1)$.

Bài giải:

a) Ta có:

$2x(x+3) – 3x^2(x+2) + x(3x^2 + 4x – 6)$

$= (2x . x + 2x . 3) – (3x^2 . x + 3x^2 . 2) + (x . 3x^2 + x . 4x – x . 6)$

$= 2x^2 + 6x – (3x^3 + 6x^2) + (3x^3 + 4x^2 – 6x)$

$= 2x^2 + 6x – 3x^3 – 6x^2 + 3x^3 + 4x^2 – 6x$

$= (– 3x^3 + 3x^3 ) + (2x^2 – 6x^2 + 4x^2 ) + (6x – 6x)$

$= 0 + 0 + 0$

$= 0$

b) Ta có:

$3x(2x^2 – x) – 2x^2(3x+1) + 5(x^2 – 1)$

$= [3x . 2x^2 + 3x . (-x)] – (2x^2 . 3x + 2x^2 . 1) + [5x^2 + 5 . (-1)]$

$= 6x^3 – 3x^2 – (6x^3 +2x^2) + 5x^2 – 5$

$= 6x^3 – 3x^2 – 6x^3 – 2x^2 + 5x^2 – 5$

$= (6x^3 – 6x^3 ) + (-3x^2 – 2x^2 + 5x^2) – 5$

$= 0 + 0 – 5$

$= – 5$

Giải bài 7.38 trang 45 Toán 7 tập 2 KNTT

Tìm giá trị của $x$ biết rằng:

a) $3x^2 – 3x(x – 2) = 36$;

b) $5x(4x^2 – 2x + 1) – 2x(10x^2 – 5x + 2) = -36$.

Bài giải:

a) Ta có:

${\rm{ }}3{x^2}–{\rm{ }}3x\left( {x{\rm{ }}–{\rm{ }}2} \right){\rm{ }} = {\rm{ }}36\\ \Leftrightarrow 3{x^2}–{\rm{ [}}3x.x + 3x.( – 2)] = 36\\ \Leftrightarrow 3{x^2} – (3{x^2} – 6x) = 36\\ \Leftrightarrow 3{x^2} – 3{x^2} + 6x = 36\\ \Leftrightarrow 6x = 36\\ \Leftrightarrow x = 36:6\\ \Leftrightarrow x = 6$

Vậy $x = 6$.

b) Ta có:

${\rm{ }}5x\left( {4{x^2}–{\rm{ }}2x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}–{\rm{ }}2x\left( {10{x^2}–{\rm{ }}5x{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }} – 36\\ \Leftrightarrow 5x.4{x^2} + 5x.( – 2x) + 5x.1 – [2x.10{x^2} + 2x.( – 5x) + 2x.2] = – 36\\ \Leftrightarrow 20{x^3} – 10{x^2} + 5x – (20{x^3} – 10{x^2} + 4x) = – 36\\ \Leftrightarrow 20{x^3} – 10{x^2} + 5x – 20{x^3} + 10{x^2} – 4x = – 36\\ \Leftrightarrow (20{x^3} – 20{x^3}) + ( – 10{x^2} + 10{x^2}) + (5x – 4x) = – 36\\ \Leftrightarrow x = – 36$

Vậy $x = -36$

Giải bài 7.39 trang 45 Toán 7 tập 2 KNTT

Thực hiện các phép tính sau:

a) $(x^3 – 8) : (x – 2)$;

b) $(x – 1)(x + 1)(x^2 + 1)$.

Bài giải:

a) Thực hiện đặt phép chia ta được:

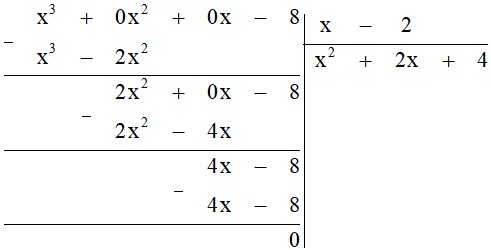
Vậy $(x^3 – 8) : (x – 2) = x^2 + 2x + 4$.

b) Ta có:

$(x – 1)(x + 1)(x^2 + 1)$

$= [x .(x + 1) – 1 .(x + 1)] . (x^2 + 1)$

$= {x.x + x.1 + (-1).x + (-1).1}. (x^2 + 1)$

$= (x^2 + x – x – 1) . (x^2 + 1)$

$= (x^2 – 1) . (x^2 + 1)$

$= x^2 . (x^2 +1) – 1.(x^2 + 1)$

$= x^2 . x^2 + x^2 . 1 – (1.x^2 + 1.1)$

$= x^4 + x^2 – (x^2 + 1)$

$= x^4 + x^2 – x^2 – 1$

$= x^4 – 1$

Vậy $(x – 1)(x + 1)(x^2 + 1) = x^4 – 1$.

Giải bài 7.40 trang 45 Toán 7 tập 2 KNTT

Trong một trò chơi ở câu lạc bộ Toán học, chủ trò viết lên bảng biểu thức:

$P(x) = x^2 (7x – 5) – (28x^5 – 20x^4 – 12x^3) : 4x^2$.

Luật chơi là sau khi chủ trò đọc một số a nào đó, các đội chơi phải tìm giá trị của $P(x)$ tại $x = a$. Đội nào tính đúng và tính nhanh nhất thì thắng cuộc.

Khi chủ trò vừa đọc $a = 5$, Vuông đã tính ngay được $P(a) = 15$ và thắng cuộc. Em có biết Vuông làm cách nào không?

Bài giải:

Ta có:

$P(x) = x^2 (7x – 5) – (28x^5 – 20x^4 – 12x^3) : 4x^2$

$= x^2 . 7x – x^2 . 5 – ( 28x^5 : 4x^2 – 20x^4 : 4x^2 – 12x^3 : 4x^2)$

$= 7x^3 – 5x^2 – (7x^3 – 5x^2 – 3x)$

$= 7x^3 – 5x^2 – 7x^3 + 5x^2 +3x$

$= (7x^3 – 7x^3 ) + (– 5x^2 + 5x^2 ) + 3x$

$= 0 +0 + 3x$

$= 3x$

Khi $x = 5$ thì $P(5) = 3 . 5 =15$

Vậy Vuông chỉ cần rút gọn biểu thức $P(x)$, sau đó thay $x = 5$ vào $P(x)$ đã rút gọn.

Giải bài 7.41 trang 45 Toán 7 tập 2 KNTT

Tìm số $b$ sao cho đa thức $x^3 – 3x^2 + 2x – b$ chia hết cho đa thức $x – 3$.

Bài giải:

Thực hiện đặt phép chia ta được:

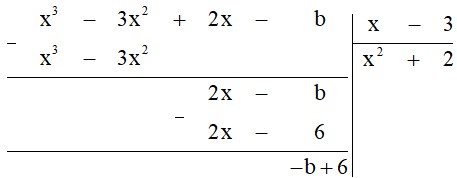
Để đa thức $x^3 – 3x^2 + 2x – b$ chia hết cho đa thức $x – 3$ thì $–b + 6 = 0$ hay $b = 6$

Vậy $b = 6$.

Bài trước:

👉 Giải bài 30 31 32 33 34 35 trang 43 sgk Toán 7 tập 2 Kết Nối Tri Thức

Bài tiếp theo:

👉 Giải bài 42 43 44 45 46 trang 46 sgk Toán 7 tập 2 Kết Nối Tri Thức

Trên đây là bài Hướng dẫn Giải bài 36 37 38 39 40 41 trang 45 sgk Toán 7 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“