Nội Dung
Hướng dẫn giải Bài Luyện tập chung sgk Toán 8 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 36 37 38 39 40 trang 56 sgk Toán 8 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
GIẢI BÀI TẬP LUYỆN TẬP CHUNG
Sau đây là phần Giải bài 36 37 38 39 40 trang 56 sgk Toán 8 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 7.36 trang 56 Toán 8 tập 2 KNTT
Cho hai hàm số $y=2x−1$ và $y=−x+2$.
a) Trong cùng mặt phẳng tọa độ $Oxy$, vẽ đồ thị của hai hàm số đã cho.
b) Tìm tọa độ giao điểm của hai đồ thị trên.
Bài giải:
a) Đồ thị hàm số $y=2x−1$ là một đường thẳng đi qua hai điểm là $(0;-1)$ và $(\frac{1}{2};0)$.
Đồ thị hàm số $y=−x+2$ là một đường thẳng đi qua hai điểm là $(0;2)$ và $(2;0)$.
Đồ thị của hai hàm số đã cho như hình sau:
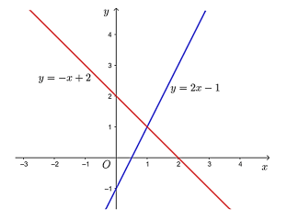
b) Phương trình hoành độ của hai hàm số là:
$2x−1=−x+2$
$⇔ 3x=3 ⇒ x=1$
Thay $x=1$ vào hàm số $y=2x−1 ⇒ y=1$
Vậy tọa đô giao điểm của hai đồ thị trên là điểm $A (1;1)$.
Giải bài 7.37 trang 56 Toán 8 tập 2 KNTT
Cho hàm số bậc nhất $y=(3−m)x+2m+1$.
Tìm các giá trị của $m$ để đồ thị của hàm số đã cho là:
a) Đường thẳng đi qua điểm $(1;2)$.
b) Đường thẳng cắt đường thẳng $y=x+1$ tại một điểm nằm trên trục tung.
Bài giải:
Hàm số $y = (3 – m)x + 2m + 1$ là hàm số bậc nhất khi $3 – m ≠ 0$, hay $m ≠ 3$.
a) Vì đồ thị đi qua điểm $(1; 2)$ nên ta có:
$2 = (3 – m).1 + 2m + 1$
$⇔ 2 = 3 – m + 2m + 1$
$⇒ m = –2.$
Giá trị này của $m$ thỏa mãn điều kiện $m ≠ 3$.
Vậy với $m = –2$ thì đồ thị của hàm số đi qua điểm $(1;2)$.
b) Vì đường thẳng $y = x + 1$ cắt trục tung tại điểm $(0; 1)$ nên để đường thẳng đã cho cắt đường thẳng $y = x + 1$ tại một điểm nằm trên trục tung thì đường thẳng $y = (3 – m)x + 2m + 1$ phải đi qua điểm $(0; 1)$. Từ đó suy ra:
$1 = (3 – m) . 0 + 2m + 1$ hay $m = 0$.
So sánh với điều kiện ta thấy $m = 0$ thỏa mãn.
Vậy với $m = 0$ thì đường thẳng đã cho cắt đường thẳng $y=x+1$ tại một điểm nằm trên trục tung.
Giải bài 7.38 trang 56 Toán 8 tập 2 KNTT
Cho đồ thị của một hàm số bậc nhất $y=f(x)$ như HÌnh 7.18.
Hãy giải các phương trình sau:
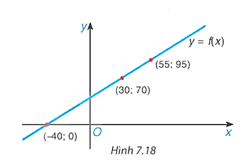
a) $f(x)=70$;
b) $f(x)=95$;
c) $f(x)=0$.
Bài giải:
Từ đồ thị đã cho, ta thấy:
a) $f(x) = 70$ khi $x = 30$;
b) $f(x) = 95$ khi $x = 55$;
c) $f(x) = 0$ khi $x = – 40$.
Giải bài 7.39 trang 56 Toán 8 tập 2 KNTT
Giá cước taxi của một hãng xe taxi khi quãng đường di chuyển $x (km)$ trong khoảng từ trên $1 km$ đến $30 km$ được cho bởi công thức sau:
$T(x) = 10 000 + 13 600.(x – 1)$ (đồng).
a) Tính số tiền phải trả khi xe di chuyển $20 km$.
b) Nếu một hành khách phải trả $200 \,400$ đồng thì hành khách đó đã di chuyển bao nhiêu kilômét?
Bài giải:
Điều kiện: $1 < x ≤ 30$.
a) Thay $x = 20$ vào công thức đã cho, ta có:
$T(20) = 10 000 + 13 600 . (20 – 1) = 268 \,400$ (đồng).
Vậy số tiền phải trả khi xe di chuyển $20 km$ là $268 \,400$ đồng.
b) Nếu một hành khách phải trả $200 \,400$ đồng, tức là $T(x) = 200 \,400$. Từ đây, ta có phương trình:
$200 \,400 = 10 \,000 + 13 \,600.(x – 1)$
$⇔ 13 \,600.(x – 1) = 190 \,400$
$⇔ x – 1 = 190 \,400 : 13 \,600$
$⇔ x – 1 = 14$
$⇔ x = 15$ (thỏa mãn điều kiện).
Vậy hành khách đó đã di chuyển $15 km$.
Giải bài 7.40 trang 56 Toán 8 tập 2 KNTT
Trong lí thuyết tài chính, giá trị sổ sách là giá trị của một tài sản mà công ty sử dụng để xây dựng bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt tài sản đó.
Giả sử một công ty vừa mua một chiếc máy photocopy mới với giá $18$ triệu đồng. Công ty lựa chọn cách tính khấu hao chiếc máy photocopy này theo phương pháp khấu hao đường thẳng trong thời gian $3$ năm, tức là mỗi năm giá trị của chiếc máy photocopy sẽ giảm $18 : 3 = 6$ triệu đồng.
a) Viết hàm số bậc nhất biểu thị giá trị sổ sách $V(x)$ của máy photocopy dưới dạng một hàm số theo thời gian sử dụng $x$ (năm) của nó.
b) Vẽ đồ thị của hàm số bậc nhất $y = V(x)$.
c) Giá trị sổ sách của máy photocopy sau $2$ năm sử dụng là bao nhiêu?
d) Sau thời gian sử dụng là bao lâu thì máy photocopy có giá trị sổ sách là $9$ triệu đồng?
Bài giải:
a) Vì mỗi năm giá trị của chiếc máy photocopy sẽ giảm $6$ triệu đồng nên $x$ năm thì giá trị của chiếc máy này sẽ giảm $6x$ triệu đồng.
Do đó, hàm số bậc nhất biểu thị giá trị sổ sách của máy photocopy là $V(x) = 18 – 6x$.
b) Vẽ đồ thị hàm số $y = V(x) = 18 – 6x$.
Cho $x = 0$ thì $y = 18$, ta được giao điểm của đồ thị với trục $Oy$ là $A(0; 18)$.
Cho $y = 0$ thì $x = 3$, ta được giao điểm của đồ thị với trục $Oy$ là $B(3; 0)$.
Đồ thị hàm số $y = 18 – 6x$ là đường thẳng $AB$.
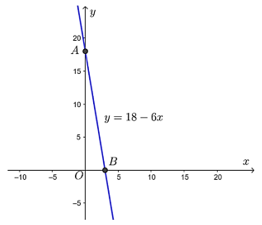
c) Giá trị sổ sách của máy sau $2$ năm sử dụng, tức với $x = 2$ là:
$V(2) = 18 – 6 . 2 = 18 – 12 = 6$ (triệu đồng).
d) Để có giá trị sổ sách là $9$ triệu đồng thì $V(x) = 9$, tức là:
$9 = 18 – 6x$, suy ra $x = 1,5$.
Vậy sau $1,5$ năm sử dụng thì máy photocopy có giá trị sổ sách là $9$ triệu đồng.
Bài trước:
👉 Giải bài 30 31 32 33 34 35 trang 54 sgk Toán 8 tập 2 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải Bài tập cuối chương VII trang 57 58 sgk Toán 8 tập 2 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 36 37 38 39 40 trang 56 sgk Toán 8 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
