Giải bài 4 5 6 7 trang 66 sgk Toán 8 tập 2 Kết Nối Tri Thức

Nội Dung

Hướng dẫn giải Bài §31. Cách tính xác suất của biến cố bằng tỉ số sgk Toán 8 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 4 5 6 7 trang 66 sgk Toán 8 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.

Bài 31 CÁCH TÍNH XÁC SUẤT CỦA BIẾN CỐ BẰNG TỈ SỐ

Bài toán mở đầu trang 63 Toán 8 tập 2 KNTT

Một túi đựng $20$ viên kẹo giống hệt nhau nhưng khác loại, trong đó có $7$ viên kẹo sữa, $4$ viên kẹo chanh, $6$ viên kẹo dừa và $3$ viên kẹo bạc hà. Bạn Lan lấy ngẫu nhiên một viên kẹo từ túi. Tính xác suất để Lan lấy được viên kẹo sữa.

Trả lời:

Có $20$ kết quả có thể của hành động trên. Bạn Lan lấy ngẫu nhiên một viên kẹo từ túi nên các kết quả có thể là đồng khả năng.

Có $7$ kết quả thuận lợi cho biến cố “Bạn Lan lấy được viên kẹo sữa”.

Vậy xác suất để Lan lấy được viên kẹo sữa là $\frac{7}{20}$.

Luyện tập 1 trang 64 Toán 8 tập 2 KNTT

Trở lại tình huống mở đầu.

Tính xác suất để Lan lấy được:

a) Viên kẹo sữa;

b) Viên kẹo chanh.

Trả lời:

Có $20$ kết quả có thể của hành động trên. Bạn Lan lấy ngẫu nhiên một viên kẹo từ túi nên các kết quả có thể là đồng khả năng.

a) Có $7$ kết quả thuận lợi cho biến cố “Bạn Lan lấy được viên kẹo sữa”.

Vậy xác suất để Lan lấy được viên kẹo sữa là $\frac{7}{20}$.

b) Có $4$ kết quả thuận lợi cho biến cố “Bạn Lan lấy được viên kẹo chanh”.

Vậy xác suất để Lan lấy được viên kẹo chanh là $\frac{4}{20} = \frac{1}{5}$.

Luyện tập 2 trang 65 Toán 8 tập 2 KNTT

Trên giá sách của thư viện có $15$ cuốn sách, trong đó có một số cuốn tiểu thuyết. Người thủ thư đặt thêm $5$ cuốn tiểu thuyết thư viện mới mua vào giá sách. Bạn Nam đến mượn sách, chọn ngẫu nhiên một cuốn sách trên giá. Biết rằng xác suất để chọn được cuốn tiểu thuyết là $\frac{3}{4}$. Hỏi lúc đầu trên giá sách có bao nhiêu cuốn tiểu thuyết?

Trả lời:

Gọi số lượng cuốn tiểu thuyết ban đầu là $x$ (cuốn).

Số lượng cuốn tiểu thuyết khi đặt thêm 5 cuốn tiểu thuyết: $x+5$ (cuốn).

Theo đề bài, ta có:

$\frac{{x + 5}}{{15 + 5}} = \frac{3}{4}$

$⇔ 4(x+5)=60$

$⇔ x+5=15$

$⇒ x=10$ (thỏa mãn)

Vậy lúc ban đầu có $10$ cuốn tiểu thuyết.

Tranh luận trang 65 Toán 8 tập 2 KNTT

Một túi đựng $17$ viên bi cùng khối lượng và kích thước, chỉ khác màu, trong đó có $8$ viên bi màu đỏ, $5$ viên bi màu xanh, $4$ viên bi màu vàng. Lấy ngẫu nhiên một viên bi từ trong túi. Tính xác suất của biến cố $E$: “lấy được viên bi màu đỏ”.

Tròn: Có $17$ viên bi nên có $17$ kết quả có thể. Có $8$ viên bi màu đỏ nên có $8$ kết quả thuận lợi cho biến cố $E$. Vậy $P(E) = \frac{8}{17}$.

Vuông: Các viên bi cùng khối lượng và kích thước, chỉ khác màu, nen chỉ có $3$ kết quả có thể là viên bi đỏ màu đỏ, viên bi màu trắng và viên bi màu vàng. Do đó $P(E) = \frac{1}{3}$.

Vuông và Tròn ai nói đúng? Tại sao?

Trả lời:

Mặc dù chỉ có ba kết quả có thể là: bi màu đỏ, bi màu trắng và bi màu vàng nhưng ba kết quả có thể này là không đồng khả năng vì số bi màu đỏ, bi màu trắng và bi màu vàng là khác nhau. Do đó, Vuông nói sai.

Các viên bi có cùng khối lượng và kích thước nhưng ta có thể đánh số các viên bi từ $1$ đến $17$. Vì chọn ngẫu nhiên nên có $17$ kết quả có thể là đồng khả năng.

Có $8$ viên bi màu đỏ nên có $8$ kết quả thuận lợi cho biến cố $E$. Vậy $P(E) = \frac{8}{17}$.

Do đó, Tròn nói đúng.

GIẢI BÀI TẬP

Sau đây là phần Giải bài 4 5 6 7 trang 66 sgk Toán 8 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 8.4 trang 66 Toán 8 tập 2 KNTT

Một tấm bìa cứng hình tròn được chia thành $20$ hình quạt như nhau, đánh số từ $1; 2;…; 20$ và được gắn vào trục quay có mũi tên cố định ở tâm (H.8.2). Quay tấm bìa và quan sát xem mũi tên chỉ vào hình quạt nào khi tấm bìa dừng lại.

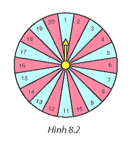
Tính xác suất để mũi tên:

a) Chỉ vào hình quạt ghi số chia hết cho $4$.

b) Chỉ vào hình quạt ghi số không phải là số nguyên tố.

Bài giải:

Có $20$ kết quả có thể, đó là $1; 2;…; 20$. Do $20$ hình quạt như nhau nên $20$ kết quả có thể này là đồng khả năng.

a) Có $4; 8; 12; 16; 20$ chia hết cho $4$ → Có $5$ hình quạt ghi số chia hết cho $4$.

Vậy xác suất để mũi tên chỉ vào hình quạt ghi số chia hết cho $4$ là: $\frac{5}{20} = \frac{1}{4}$.

b) Có số $1; 4; 6; 8; 9; 10; $ $12; 14; 15; 16; 18; 20$ không phải số nguyên tố → Có $12$ hình quạt ghi số không phải là số nguyên tố.

Vậy xác suất để mũi tên chỉ vào hình quạt ghi số không phải là số nguyên tố là: $\frac{12}{20} = \frac{3}{5}$.

Giải bài 8.5 trang 66 Toán 8 tập 2 KNTT

Một túi đựng các viên kẹo giống hệt nhau, chỉ khác màu, trong đó có $5$ viên kẹo màu đen, $3$ viên kẹo màu đỏ, $7$ viên kẹo màu trắng. Lấy ngẫu nhiên một viên kẹo trong túi.

Tính xác suất của các biến cố sau:

a) $E$: “Lấy được viên kẹo màu đen”;

b) $F$: “Lấy được viên kẹo màu đen hoặc màu đỏ”;

c) $G$: “Lấy được viên kẹo màu trắng”;

d) $H$: “Không lấy được viên kẹo màu đỏ”.

Bài giải:

Trong túi có $5 + 3 + 7 = 15$ (viên kẹo). Do đó, số kết quả có thể là $15$.

Vì lấy ngẫu nhiên nên $15$ kết quả có thể nảy là đồng khả năng.

a) Túi có $5$ viên kẹo màu đen. Vậy có $5$ kết quả thuận lợi cho $E$.

Do đó $P(E) = \frac{5}{15} = \frac{1}{3}$.

b) Túi có $5$ viên kẹo màu đen và $3$ viên kẹo màu đỏ. Vậy có $5 + 3 = 8$ kết quả thuận lợi cho $F$.

Do đó $P(F) = \frac{8}{15}$.

c) Túi có $7$ viên kẹo màu trắng. Vậy có $7$ kết quả thuận lợi cho $G$.

Do đó $P(G) = \frac{7}{15}$.

d) Túi có $5$ viên kẹo màu đen và $7$ viên kẹo màu trắng, tức là có $5 + 7 = 12$ viên kẹo không phải màu đỏ. Vậy có $5 + 7 = 12$ kết quả thuận lợi cho $H$.

Do đó $P(H) = \frac{12}{15} = \frac{4}{5}$.

Giải bài 8.6 trang 66 Toán 8 tập 2 KNTT

Trong một chiếc hộp có $15$ tấm thẻ giống nhau được đánh số $10; 11;…; 24$. Rút ngẫu nhiên một tấm thẻ từ trong hộp. Tính xác suất của các biến cố sau:

a) $A$: “Rút được tấm thẻ ghi số lẻ”;

b) $B$: “Rút được tấm thẻ ghi số nguyên tố”.

Bài giải:

Có $15$ kết quả có thể xảy ra. Do $15$ tấm thẻ giống nhau nên $15$ kết quả có thể này là đồng khả năng.

a) Có $11; 13; 15; 17; 19; 21; 23$ là số lẻ → Có $7$ kết quả thuận lợi cho biến cố $A$.

Do đó xác suất của biến cố $A$ là $P(A) = \frac{7}{15}$.

b) Có $11; 13; 17; 19; 23$ là số nguyên tố → Có $5$ kết quả thuận lợi cho biến cố $B$.

Do đó xác suất của biến cố $B$ là $P(B) = \frac{5}{15} = \frac{1}{3}$.

Giải bài 8.7 trang 66 Toán 8 tập 2 KNTT

Trò chơi vòng quay may mắn.

Một bánh xe hình tròn được chia thành $12$ hình quạt như nhau, trong đó có $2$ hình quạt ghi $100$ điểm, $2$ hình quạt ghi $200$ điểm, $2$ hình quạt ghi $300$ điểm, $2$ hình quạt ghi $400$ điểm, $1$ hình quạt ghi $500$ điểm, $2$ hình quạt ghi $1 \,000$ điểm, $1$ hình quạt ghi $2 \,000$ điểm (H.8.3). Ở mỗi lượt, người chơi quay bánh xe. Mũi tên cố định gắn trên vành bánh xe dừng ở hình quạt nào thì người chơi nhận được số điểm ghi trên hình quạt đó.

Bạn Lan chơi trò chơi này. Tính xác suất của biến cố sau:

a) $A$: “Trong một lượt quay, Lan quay được $400$ điểm”;

b) B: “Trong một lượt quay, Lan được ít nhất $500$ điểm”.

Bài giải:

Có $12$ kết quả có thể xảy ra. Do $12$ bánh xe như nhau nên $12$ kết quả có thể này là đồng khả năng.

a) Có $2$ hình quạt $400$ điểm → Có $2$ kết quả thuận lợi cho biến cố $A$.

Do đó, xác suất của biến cố $A$ là $P(A) = \frac{2}{12} = \frac{1}{6}$.

b) Có $1$ hình quạt ghi $500$ điểm, $2$ hình quạt ghi $1 \,000$ điểm, $1$ hình quạt ghi $2 \,000$ điểm → Có $4$ kết quả thuận lợi cho biến cố $B$.

Do đó, xác suất của biến cố $B$ là $P(B) = \frac{4}{12} = \frac{1}{3}$.

Bài trước:

👉 Giải bài 1 2 3 trang 62 sgk Toán 8 tập 2 Kết Nối Tri Thức

Bài tiếp theo:

👉 Giải bài 8 9 10 11 12 13 trang 71 72 sgk Toán 8 tập 2 Kết Nối Tri Thức

Trên đây là bài Hướng dẫn Giải bài 4 5 6 7 trang 66 sgk Toán 8 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“