Nội Dung
Hướng dẫn giải Bài tập cuối chương 2 sgk Toán 8 tập 1 bộ Chân Trời Sáng Tạo. Nội dung bài bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
GIẢI BÀI TẬP CUỐI CHƯƠNG 2
Sau đây là phần Giải Bài tập cuối chương 2 trang 54 55 56 sgk Toán 8 tập 1 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
CÂU HỎI TRẮC NGHIỆM
Giải bài 1 trang 54 Toán 8 tập 1 CTST
Trong các phát biểu sau, phát biểu nào sai?
Hình chóp tam giác đều có:
A. ba cạnh bên bằng nhau.
B. các cạnh bên bằng nhau và đáy là hình tam giác có ba góc bằng nhau.
C. tất cả các cạnh bên bằng nhau và đáy là tam giác đều.
D. tất cả các cạnh đều bằng nhau.
Trả lời:
Hình chóp tam giác đều có
– ba cạnh bên bằng nhau;
– đáy là tam giác đều nên ba góc bằng nhau và ba cạnh đáy bằng nhau.
Do đó cạnh bên và cạnh đáy của hình chóp tam giác đều có thể không bằng nhau hoặc bằng nhau, nên phương án D là sai.
⇒ Đáp án: D.
Giải bài 2 trang 54 Toán 8 tập 1 CTST
Trong các phát biểu sau, phát biểu nào đúng?
Hình chóp tứ giác đều có:
A. các mặt bên là tam giác đều.
B. tất cả các cạnh bằng nhau.
C. các cạnh bên bằng nhau và đáy là hình vuông.
D. các mặt bên là tam giác vuông.
Trả lời:
Hình chóp tứ giác đều có:
– bốn cạnh bên bằng nhau;
– đáy là hình vuông;
– các mặt bên là các tam giác cân.
nên phương án C là đúng.
⇒ Đáp án: C.
Giải bài 3 trang 54 Toán 8 tập 1 CTST
Trong các phát biểu sau, phát biểu nào đúng?
Chiều cao của hình chóp tam giác đều là:
A. độ dài đoạn thẳng nối từ đỉnh của hình chóp tới trung điểm của một cạnh đáy.
B. chiều cao của mặt đáy.
C. độ dài đường trung tuyến của một mặt bên của hình chóp.
D. độ dài đoạn thẳng nối từ đỉnh tới trọng tâm của tam giác đáy..
Trả lời:
Chiều cao của hình chóp tam giác đều là độ dài đoạn thẳng nối từ đỉnh tới trọng tâm của tam giác đáy.
⇒ Đáp án: D.
Giải bài 4 trang 54 Toán 8 tập 1 CTST
Hình chóp tam giác đều có diện tích đáy là \(30 \,cm^2\), mỗi mặt bên có diện tích \(42 \,cm^2\), có diện tích toàn phần là:
A. \(126 \,cm^2\).
B. \(132 \,cm^2\).
C. \(90 \,cm^2\).
D. \(156 \,cm^2\).
Trả lời:
Diện tích toàn phần của hình chóp tam giác đều:
\(S_{tp} = S_{xq} + S_{đáy} = 42.3 + 30 = 156 \,cm^2\)
⇒ Đáp án: D.
Giải bài 5 trang 54 Toán 8 tập 1 CTST
Hình chóp tứ giác đều có diện tích đáy là \(30 \,m^2\), chiều cao \(100 \,dm\), có thể tích là:
A. \(100 \,m^3\).
B. \(300 \,m^3\).
C. \(1000 \,m^3\).
D. \(300 \,dm^3\).
Trả lời:
Đổi \(100 dm = 10 m\)
Thể tích của hình chóp là:
\(V = \frac{1}{3}.S_{đáy}.h = \frac{1}{3}.30.10 = 100 \,m^3\).
⇒ Đáp án: A.
BÀI TẬP TỰ LUẬN
Giải bài 6 trang 55 Toán 8 tập 1 CTST
Trong các tấm bìa ở Hình 1, tấm bìa nào gấp được hình chóp tam giác đều, tấm bìa nào gấp được hình chóp tứ giác đều?
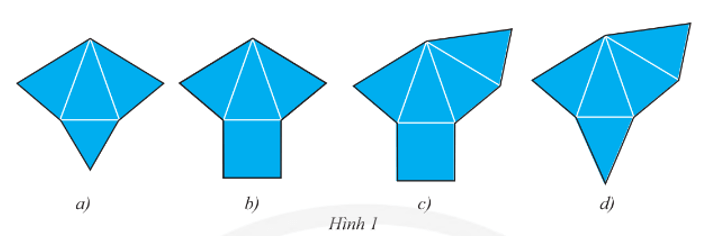
Bài giải:
Tấm bìa ở Hình 1a) gấp được hình chóp tam giác đều vì có đáy là tam giác đều, 3 mặt bên là các tam giác cân.
Tấm bìa ở Hình 1c) gấp được hình chóp tứ giác đều vì có đáy là tứ giác đều (hình vuông) và 4 mặt bên là các tam giác cân.
Giải bài 7 trang 55 Toán 8 tập 1 CTST
Quan sát hình chóp tam giác đều ở Hình 2 và cho biết:
a) Đỉnh, mặt đáy và các mặt bên của hình đó.
b) Độ dài cạnh \(MA\) và cạnh \(BC\).
c) Đoạn thẳng nào là đường cao của hình đó.
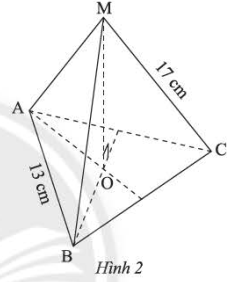
Bài giải:
Hình chóp tam giác đều ở Hình 2 có:
a) Đỉnh: \(M\)
Mặt đáy: \(ABC\)
Các mặt bên: \(MAB\); \(MAC\); \(MBC\)
b) Các cạnh bên bằng nhau: \(MA = MC = 17\) cm
Các cạnh đáy bằng nhau: \(BC = AB = 13\) cm
c) Đoạn thẳng \(MO\) là đường cao của hình chóp tam giác đều \(M.ABC\)
Giải bài 8 trang 55 Toán 8 tập 1 CTST
Quan sát hình chóp tứ giác đều ở Hình 3 và cho biết:
a) Mặt đáy và các mặt bên của hình đó.
b) Độ dài cạnh \(IB\) và cạnh \(BC\)
c) Đoạn thẳng nào là đường cao của hình đó.
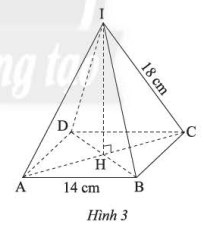
Bài giải:
Hình chóp tứ giác đều ở Hình 3 có:
a) Mặt đáy: \(ABCD\)
Các mặt bên: \(IAD\); \(IAB\); \(IBC\); \(ICD\)
b) Các cạnh bên bằng nhau: \(IB = IC = 18\) cm
Các cạnh đáy bằng nhau: \(BC = AB = 14\) cm
c) Đoạn thẳng \(IH\) là đường cao của hình chóp \(S.ABCD\).
Giải bài 9 trang 55 Toán 8 tập 1 CTST
Tính diện tích xung quanh, diện tích toàn phần và thể tích của:
a) Hình chóp tam giác đều có chiều cao là \(98,3\) cm; tam giác đáy có độ dài cạnh là \(40\) cm và chiều cao là \(34,6\) cm; chiều cao mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là \(99\) cm.
b) Hình chóp tứ giác đều có độ dài cạnh đáy là \(120\) cm, chiều cao là \(68,4\) cm, chiều cao mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều là \(91\) cm.
Bài giải:
a) Ta có hình vẽ minh họa sau:
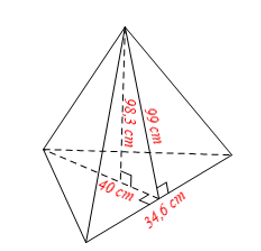
Diện tích xung quanh của hình chóp tam giác đều là:
\(S_{xq} = \frac{{99.40}}{2}.3 = 5940 \,cm^2\)
Diện tích đáy của hình chóp là:
\(S_{đáy} = \frac{{40.34,6}}{2} = 692 \,cm^2\)
Diện tích toàn phần của hình chóp là:
\(S_{tp} = S_{xq} + S_{đáy} = 5940 + 692 = 6632 \,cm^2\)
Thể tích của hình chóp là:
\(V = \frac{1}{3}.S_{đáy}.h = \frac{1}{3}.692.98,3 \approx 22674,53 \,cm^3\).
b) Ta có hình vẽ minh họa sau:
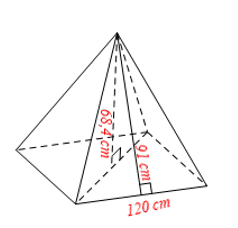
Diện tích xung quanh của hình chóp tứ giác đều là:
\(S_{xq} = \frac{{91.120}}{2}.4 = 21840 \,cm^2\)
Diện tích đáy của hình chóp là:
\(S_{đáy} = 120.120 = 14400 \,cm^2\)
Diện tích toàn phần của hình chóp là:
\(S_{tp} = S_{xq} + S_{đáy} = 21840 + 14400 = 36240 \,cm^2\)
Thể tích của hình chóp là:
\(V = \frac{1}{3}.S_{đáy}.h = \frac{1}{3}.14400.68,4 = 328320 \,cm^3\).
Giải bài 10 trang 56 Toán 8 tập 1 CTST
Tính thể tích khối rubik có dạng hình chóp tam giác đều (Hình 4). Biết khối rubik này có bốn mặt là các tam giác đều bằng nhau cạnh \(6\) cm và chiều cao \(3\sqrt 3\) cm; chiều cao của khối rubik bằng \(2\sqrt 6\) cm.

Bài giải:
Diện tích đáy của khối rubik có dạng hình chóp tam giác đều là:
\(S_{đáy} = \frac{{(3\sqrt 3).6}}{2} = 9\sqrt 3 \,cm^2\)
Thể tích của khối rubik có dạng hình chóp tam giác đều là:
\(V = \frac{1}{3}.S_{đáy}.h = \frac{1}{3}.9\sqrt 3.2\sqrt 6 ≈ 25,46 \,cm^3\)
Giải bài 11 trang 56 Toán 8 tập 1 CTST
Lớp bạn Na dự định gấp \(100\) hộp đựng quà dạng hình chóp tam giác đều có tất cả các mặt đều là hình tam giác đều cạnh \(5\) cm để đựng các món quà gửi tặng cho học sinh khó khăn dịp Tết Trung thu. Cho biết chiều cao của mỗi mặt là \(4,3\) cm. Tính diện tích giấy cần để làm hộp, biết rằng phải tốn \(20\% \) diện tích giấy cho các mép giấy và các phần bị bỏ đi.
Bài giải:
Ta có hình vẽ minh họa sau:
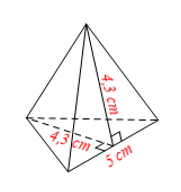
Diện tích toàn phần của 1 hộp là:
\(\frac{{5.4,3}}{2}.4 = 43 \,cm^2\)
Diện tích toàn phần của 100 hộp là:
\(43.100 = 4300 \,cm^2\)
Diện tích giấy cho các mép giấy và các phần giấy bỏ đi là:
\(4300.20\% = 860 \,cm^2\)
Diện tích giấy cần để làm hộp là:
\(4300 + 860 = 5160 \,cm^2\)
Giải bài 12 trang 56 Toán 8 tập 1 CTST
Một bể kính hình hộp chữ nhật chứa nước có hai cạnh đáy là \(50\) cm và \(40\) cm, khoảng cách từ mực nước tới miệng bể là \(15\) cm. Người ta dự định đặt vào bể một khối đá hình chóp tứ giác đều cạnh đáy là \(20\) cm, chiều cao \(15\) cm. Khi đó khoảng cách mực nước tới miệng bể là bao nhiêu? Biết rằng bề dày của đáy bể và thành bể không đáng kể, sau khi đặt khối đá vào, nước ngập khối đá và không tràn ra ngoài.
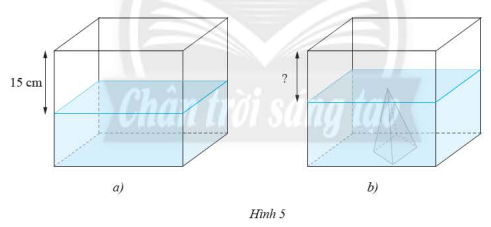
Bài giải:
Lượng nước cần đổ vào bể để bể chứa đầy nước là:
\(V_1 = 50.40.15 = 30000 \,cm^3\)
Thể tích khối đá là:
\(V_2 = \frac{1}{3}.20.20.15 = 2000 \,cm^3\)
Lượng nước cần đổ vào bể (sau khi có khối đá) để bể chứa đầy nước là:
\(V = V_1 – V_2 = 30000 – 2000 = 28000 \,cm^3\)
Khoảng cách mực nước tới miệng bể là:
\(h = \frac{V}{S_{đáy}} = \frac{28000}{50.40} = 14 \,(cm)\)
Bài trước:
👉 Giải bài 1 2 3 4 trang 52 53 sgk Toán 8 tập 1 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 trang 61 62 sgk Toán 8 tập 1 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải Bài tập cuối chương 2 trang 54 55 56 sgk Toán 8 tập 1 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
