Nội Dung
Hướng dẫn giải Bài tập cuối chương VII sgk Toán 8 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải Bài tập cuối chương VII trang 57 58 sgk Toán 8 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
GIẢI BÀI TẬP CUỐI CHƯƠNG VII
Sau đây là phần Giải Bài tập cuối chương VII trang 57 58 sgk Toán 8 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
A. TRẮC NGHIỆM
Giải bài 7.41 trang 57 Toán 8 tập 2 KNTT
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
A. $0x+2=0$.
B. $2x+1=2x+2$.
C.$2x^2+1=0$.
D. $3x−1=0$.
Trả lời:
Phương trình $3x – 1 = 0$ là phương trình bậc nhất một ẩn vì $a ≠ 0$ và bậc của phương trình là $1$.
⇒ Đáp án: D.
Giải bài 7.42 trang 57 Toán 8 tập 2 KNTT
Tập nghiệm $S$ của phương trình $3(x+1)−(x−2)=7−2x$ là
A. $S=0$.
B. $S={\frac{1}{2}}$.
C. $S=∅$.
D. $S=R$.
Trả lời:
Ta có:
$3(x+1)−(x−2)=7−2x$
$⇔ 3x+3−x+2=7−2x$
$⇔ 4x=2$
\(⇒ x = \frac{1}{2}\)
Vậy tập nghiệm của phương trình là $S=\{\frac{1}{2}\}$.
⇒ Đáp án: B.
Giải bài 7.43 trang 57 Toán 8 tập 2 KNTT
Hàm số nào nào sau đây là hàm số bậc nhất?
A. $y=0x+3$.
B. $y= 3x^2+2$.
C. $y=2x$.
D. $y=0$.
Trả lời:
Hàm số $y = 2x$ là hàm số bậc nhất một ẩn vì $a ≠ 0$ và bậc của phương trình là $1$.
⇒ Đáp án: C.
Giải bài 7.44 trang 57 Toán 8 tập 2 KNTT
Đường thẳng có hệ số góc bằng $2$ và đi qua điểm $(-1;2)$ là:
A. $y=2x+2$.
B. $y=2x−1$.
C. $y=−x+2$.
D. $y=2x+4$.
Trả lời:
Vì đường thẳng có hệ số góc là $2$ nên đường thẳng này có dạng $y = 2x + b$.
Lại có đường thẳng đi qua điểm $(–1; 2)$, thay $x = –1; y = 2$ vào $y = 2x + b$ ta được:
$2 = 2 . (– 1) + b$, suy ra $b = 4$.
Vậy ta có đường thẳng cần tìm là $y = 2x + 4$.
⇒ Đáp án: D.
Giải bài 7.45 trang 57 Toán 8 tập 2 KNTT
Giá trị $m$ để đường thẳng $y=(m+1)x+2$ song song với đường thẳng $y=−2x$ là
A. $m=−3$.
B. $m=−2$.
C. $m=2$.
D. $m=1$.
Trả lời:
Hai đường thẳng đã cho song song với nhau khi $m + 1 = –2$, tức là $m = –3$.
⇒ Đáp án: A.
B. TỰ LUẬN
Giải bài 7.46 trang 57 Toán 8 tập 2 KNTT
Giải các phương trình sau:
a) $5(x−1)−(6−2x)=8x−3$;
b) $\frac{2x – 1}{3} – \frac{5 – 3x}{2} = \frac{x + 7}{4}$.
Bài giải:
a) Ta có:
$5(x−1)−(6−2x)=8x−3$
$⇔ 5x−5−6+2x=8x−3$
$⇔ −x=8$
$⇒ x=−8$
Vậy tập nghiệm của phương trình là $S=\{-8\}$.
b) Ta có:
$\frac{2x – 1}{3} – \frac{5 – 3x}{2} = \frac{x + 7}{4}$
$⇔ \frac{4(2x – 1)}{12} – \frac{6(5 – 3x)}{12} = \frac{3(x + 7)}{12}$
$⇔ 8x – 4 – 30 + 18x = 3x + 21$
$⇔ 8x + 18x – 3x = 21 + 4 + 30$
$⇔ 23x = 55$
$⇒ x = \frac{55}{23}$
Vậy tập nghiệm của phương trình là $S=\{\frac{55}{23}\}$.
Giải bài 7.47 trang 57 Toán 8 tập 2 KNTT
Số tiền thuế thu nhập cá nhân khi mức thu nhập chịu thuế trong năm trong khoảng từ trên $60$ triệu đồng đến $120$ triệu đồng được cho bởi công thức sau:
$T(x)=0,1x−3$ (triệu đồng)
trong đó $60<x≤120$ (triệu đồng) là mức thu nhập chịu thuế của người đó trong năm.
a) Tính số thuế thu nhập phải đóng khi mức thu nhập chịu thuế trong năm là $100$ triệu đồng.
b) Nếu một người phải đóng $8$ triệu đồng tiền thuế thu nhập cá nhân thì mức thu nhập chịu thuế của người đó trong năm là bao nhiêu, biết rằng người đó có thu nhập chịu thuế trong khoảng từ trên $60$ triệu đồng đến $120$ triệu đồng?
Bài giải:
a) Số thuế thu nhập phải đóng khi mức thu nhập chịu thuế trong năm là $100$ triệu đồng:
$T(100) = 0,1 . 100 – 3 = 7$ (triệu đồng).
b) Nếu một người phải đóng $8$ triệu đồng tiền thuế thu nhập cá nhân nghĩa là $T(x) = 8$, tức là $0,1x – 3 = 8$, suy ra $x = 110$ (thỏa mãn điều kiện của đề bài).
Vậy người đó có thu nhập chịu thuế là $110$ triệu đồng.
Giải bài 7.48 trang 58 Toán 8 tập 2 KNTT
Một cửa hàng sách giảm giá $20\%$ cho một cuốn sách. Vì là khách quen của cửa hàng nên bạn An được giảm thêm $10\%$ trên giá đã giảm, do đó chỉ phải trả $36 \,000$ đồng cho cuốn sách đó. Hỏi giá ban đầu của cuốn sách đó nếu không giảm giá là bao nhiêu?
Bài giải:
Gọi $x$ (nghìn đồng) là giá ban đầu của cuốn sách đó. $(x > 36)$
Khi đó, theo chương trình khuyến mại, cuốn sách đó được giảm giá $0,2x$ (nghìn đồng), do vậy số tiền của cuốn sách lúc này là $x – 0,2x = 0,8x$ (nghìn đồng).
Số tiền được giảm giá theo chương trình khách hàng thân thiết là:
$0,1 . 0,8x = 0,08x$ (nghìn đồng).
Như vậy, tổng số tiền bạn An được giảm giá là $0,2x + 0,08x = 0,28x$ (nghìn đồng).
Do bạn An chỉ trả $36$ nghìn đồng nên ta có phương trình:
$x – 0,28x = 36$
$⇔ 0,72x = 36$
$⇔ x = \frac{36}{0,72}$
$⇒ x = 50$ (thỏa mãn).
Vậy giá ban đầu của cuốn sách đó là $50$ nghìn đồng.
Giải bài 7.49 trang 58 Toán 8 tập 2 KNTT
Hai ô tô cùng xuất phát từ Hà Nội đi Hạ Long lúc $8$ giờ sáng, trên cùng một tuyến đường. Vận tốc của một ô tô lớn hơn $5$ km/h so với ô tô kia. Xe đi nhanh hơn đến Hạ Long lúc $10$ giờ $45$ phút sáng, trước xe kia $15$ phút. Hỏi vận tốc của mỗi ô tô là bao nhiêu? Tính độ dài quãng đường từ Hà Nội đến Hạ Long.
Bài giải:
Thời gian di chuyển của ô tô đi nhanh hơn là:
$10$ giờ $45$ phút $– 8$ giờ = $2$ giờ $45$ phút = $2,75$ giờ.
Ta có $15$ phút = $0,25$ giờ.
Thời gian di chuyển của ô tô đi chậm hơn là: $2,75 + 0,25 = 3$ (giờ).
Gọi vận tốc ô tô đi chậm hơn là $x (km/h)$. Điều kiện $x > 0$.
Vận tốc của ô tô đi nhanh hơn là: $x + 5$ (km/h).
Quãng đường di chuyển của ô tô đi nhanh hơn là: $2,75(x + 5)$ (km).
Quãng đường di chuyển của ô tô đi chậm hơn là: $3x$ (km).
Vì quãng đường hai xe đi được là như nhau nên ta có phương trình:
$2,75(x + 5) = 3x$
Giải phương trình trên như sau:
$2,75(x + 5) = 3x$
$⇔ 2,75x + 13,75 = 3x$
$⇔ 3x – 2,75x = 13,75$
$⇔ 0,25x = 13,75$
$⇒ x = 55$ (thỏa mãn điều kiện).
Vận tốc của ô tô đi chậm hơn là $55$ km/h.
Vận tốc của ô tô đi nhanh hơn là $55 + 5 = 60$ (km/h).
Quãng đường từ Hà Nội đến Hạ Long dài $3 . 55 = 165 km$.
Giải bài 7.50 trang 58 Toán 8 tập 2 KNTT
Cho hàm số bậc nhất $y=(m+2)x+3$.
a) Tìm $m$ để đồ thị hàm số song song với đường thẳng $y=−x$.
b) Vẽ đồ thị hàm số với giá trị $m$ tìm được ở câu a.
c) Tìm giao điểm $A$ của đồ thị hàm số tìm được ở câu a và đồ thị của hàm số $y=x+1$. Tính diện tích của tam giác $OAB$, trong đó $B$ là giao điểm của đồ thị hàm số $y=x+1$ với trục $Ox$.
Bài giải:
Hàm số $y = (m + 2)x + 3$ là hàm số bậc nhất khi $m + 2 ≠ 0$, hay $m ≠ – 2$.
Vậy ta có điều kiện $m ≠ – 2$.
a) Đồ thị hàm số đã cho song song với đường thẳng $y = –x$ khi $m + 2 = –1$, tức là $m = –3$.
Giá trị này thỏa mãn điều kiện $m ≠ – 2$.
Vậy với $m = –3$ thì đồ thị hàm số song song với đường thẳng $y=−x$.
b) Với $m = –3$ ta có hàm số $y = –x + 3$.
Đồ thị hàm số $y = –x + 3$ là đường thẳng đi qua hai điểm $(0; 3)$ và $(3; 0)$.
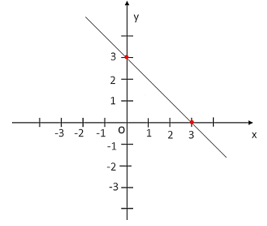
c) Giao điểm của đồ thị hàm số tìm được ở câu a với đồ thị của hàm số $y = x + 1$ là $A(1; 2)$.
Giao điểm của đồ thị hàm số $y = x + 1$ với trục hoành là $B(-1; 0)$.
Do đó $OB = 1$.
Gọi $H$ là chân đường vuông góc hạ từ $A$ xuống trục hoành.

Ta có: $H(1, 0)$ và $AH = |yA| = 2$.
Diện tích tam giác $OAB$ là:
$S_{OAB} = \frac{1}{2}AH.OB = \frac{1}{2}.2.1 = 1$ (đơn vị diện tích).
Bài trước:
👉 Giải bài 36 37 38 39 40 trang 56 sgk Toán 8 tập 2 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 1 2 3 trang 62 sgk Toán 8 tập 2 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải Bài tập cuối chương VII trang 57 58 sgk Toán 8 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
