Nội Dung
Hướng dẫn giải Bài tập ôn tập cuối năm sgk Toán 7 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải Bài tập ôn tập cuối năm sgk Toán 7 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
GIẢI BÀI TẬP ÔN TẬP CUỐI NĂM
SỐ VÀ ĐẠI SỐ
Giải bài 1 trang 110 Toán 7 tập 2 KNTT
Tính giá trị của các biểu thức sau:
a) $\sqrt{25} + {(2^2.3)}^2.{(-\dfrac{1}{4})}^2 + 2020^0 + |-\dfrac{1}{4}|$;
b) $\dfrac{3^2 – 0,25.(7,5 – 5,1)}{-6,2 + 2.(0,5 + 1,6)}$.
Bài giải:
a) Ta có:
$\sqrt{25} + {(2^2.3)}^2.{(-\dfrac{1}{4})}^2 + 2020^0 + |-\dfrac{1}{4}|$
$= 5 + {(4.3.(-\dfrac{1}{4}))}^2 + 1 + \dfrac{1}{4}$
$= 5 + {(-3)}^2 + 1 + \dfrac{1}{4}$
$= 15 + \dfrac{1}{4}$
$= \dfrac{60}{4} + \dfrac{1}{4}$
$= \dfrac{61}{4}$
b) Ta có:
$\dfrac{3^2 – 0,25.(7,5 – 5,1)}{-6,2 + 2.(0,5 + 1,6)}$
$= \dfrac{9 – 0,25.2,4}{-6,2 + 2.2,1}$
$= \dfrac{9 – 0,6}{-6,2 + 4,2}$
$= \dfrac{8,4}{-2}$
$= – 4,2$
Giải bài 2 trang 110 Toán 7 tập 2 KNTT
Tính một cách hợp lí.
a) $\dfrac{5}{11} − \dfrac{10}{19} +1,5 + \dfrac{17}{11} − \dfrac{9}{19}$;
b) $2\dfrac{3}{5}.(−\dfrac{2}{3}) − 2\dfrac{1}{3}.(−\dfrac{2}{3}) + {(\dfrac{2}{3})}^2$.
Bài giải:
Ta có thể tính như sau:
a) $\dfrac{5}{11} − \dfrac{10}{19} +1,5 + \dfrac{17}{11} − \dfrac{9}{19}$
$= (\dfrac{5}{11} + \dfrac{17}{11}) +1,5 − (\dfrac{9}{19} + \dfrac{10}{19})$
$= \dfrac{22}{11} +1,5 − \dfrac{19}{19}$
$= 2 + 1,5 – 1$
$= 2,5$
b) $2\dfrac{3}{5}.(−\dfrac{2}{3}) − 2\dfrac{1}{3}.(−\dfrac{2}{3}) + {(\dfrac{2}{3})}^2$
$= 2\dfrac{3}{5}.(−\dfrac{2}{3}) − 2\dfrac{1}{3}.(−\dfrac{2}{3}) + {(-\dfrac{2}{3})}^2$
$= (−\dfrac{2}{3}).(2\dfrac{3}{5} − 2\dfrac{1}{3} − \dfrac{2}{3})$
$= \dfrac{-2}{3}.(2\dfrac{3}{5} − 2 − \dfrac{1}{3} − \dfrac{2}{3})$
$= \dfrac{-2}{3}.(2 + \dfrac{3}{5} − 2\dfrac{1}{3} − \dfrac{2}{3})$
$= \dfrac{-2}{3}.(2 – 2 + \dfrac{3}{5} − \dfrac{1}{3} − \dfrac{2}{3})$
$= \dfrac{-2}{3}.(\dfrac{3}{5} − 1)$
$= \dfrac{-2}{3}.\dfrac{-2}{5}$
$= \dfrac{4}{15}$
Giải bài 3 trang 110 Toán 7 tập 2 KNTT
a) Tìm $x$, biết $\dfrac{2}{5}x + \dfrac{3}{2} = \dfrac{3}{5} − (−\dfrac{1}{4})$.
b) Có hay không số $x$ thỏa mãn điều kiện: $|x| + \dfrac{1}{5} = −(\dfrac{1}{2} − \dfrac{1}{3})$?
c) Hãy ước tính (không tra bảng hay dùng máy tính) số dương $x$ (lấy đến 1 chữ số sau dấu phẩy) sao cho $x^2 = 13$. Sau đó dùng máy tính cầm tay (hoặc tra bảng) để tính $x$, chính xác đến hàng phần chục để kiểm tra xem con số em ước tính chênh lệch bao nhiêu so với kết quả tính bằng máy tính.
Bài giải:
a) Ta có:
$\dfrac{2}{5}x + \dfrac{3}{2} = \dfrac{3}{5} − (−\dfrac{1}{4})$
$⇔ \dfrac{2}{5}x + \dfrac{3}{2} = \dfrac{3}{5} + \dfrac{1}{4}$
$⇔ \dfrac{2}{5}x = \dfrac{3}{5} + \dfrac{1}{4} – \dfrac{3}{2}$
$⇔ \dfrac{2}{5}x = \dfrac{12}{20} + \dfrac{5}{20} – \dfrac{30}{20}$
$⇔ \dfrac{2}{5}x = \dfrac{-13}{20}$
$⇔ x = \dfrac{-13}{20} : \dfrac{2}{5}$
$⇔ x = \dfrac{-13}{20} . \dfrac{5}{2}$
$⇔ x = \dfrac{-13}{8}$
Vậy $x = \dfrac{-13}{8}$.
b) Ta có:
$−(\dfrac{1}{2} − \dfrac{1}{3}) = −(\dfrac{3}{6} − \dfrac{2}{6}) = −\dfrac{1}{6} < 0$
Mà $|x| ≥ 0$ với mọi giá trị của $x$ nên $|x| + \dfrac{1}{5} > 0$ với mọi giá trị của $x$
Do đó không tồn tại giá trị của $x$ để $|x| + \dfrac{1}{5} = −(\dfrac{1}{2} − \dfrac{1}{3})$.
c) Ta thấy $3^2 = 9 < 13 < 16 = 4^2$ và $13 – \dfrac{1}{2}(9 + 16) < 1$ nên dự đoán $x ≈ \dfrac{1}{2}(3 + 4) = 3,5$.
Sử dụng máy tính cầm tay, lấy chính xác đến hàng phần chục ta được $\sqrt{13} ≈ 3,6$.
Con số ước tính chênh lệch $3,6 – 3,5 = 0,1$ so với kết quả tính bằng máy tính.
Giải bài 4 trang 110 Toán 7 tập 2 KNTT
Hai người thợ cùng làm tổng cộng được 136 sản phẩm (thời gian làm như nhau). Hỏi mỗi người thợ làm được bao nhiêu sản phẩm, biết rằng người thợ thứ nhất làm một sản phẩm mất 9 phút, còn người thứ hai làm mất 8 phút?
Bài giải:
Gọi số sản phẩm làm được của người thứ nhất và người thứ hai lần lượt là $x$ và $y$ sản phẩm (x, y ∈ ℕ*).
Tỉ lệ thời gian làm được 1 sản phẩm của người thứ nhất và người thứ hai là $\dfrac{9}{8}$.
Thời gian làm và số sản phẩm làm được của hai người là hai đại lượng tỉ lệ nghịch.
Do đó tỉ lệ số sản phẩm làm được của người thứ nhất và người thứ hai là $\dfrac{8}{9}$.
Khi đó $\dfrac{x}{y} = \dfrac{8}{9}$ nên $\dfrac{x}{8} = \dfrac{y}{9}$
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
$\dfrac{x}{8} = \dfrac{y}{9} = \dfrac{x + y}{8 + 9} = \dfrac{136}{17} = 8$
Khi đó $⇒ x = 8 . 8 = 64$, $y = 8 . 9 = 72$.
Vậy số sản phẩm làm được của người thứ nhất và người thứ hai lần lượt là $64$ sản phẩm và $72$ sản phẩm.
Giải bài 5 trang 110 Toán 7 tập 2 KNTT
Ba khối 6, 7, 8 của một trường Trung học cơ sở tham gia quyên góp vở tặng các bạn vùng khó khăn. Biết rằng số vở quyên góp được của ba khối theo thứ tự tỉ lệ thuận với 8, 7, 6 và số vở khối 8 quyên góp được ít hơn số vở khối 6 quyên góp được là 80 quyển. Hỏi mỗi khối quyên góp được bao nhiêu quyển vở?
Bài giải:
Gọi số vở quyên góp được của ba khối 6, 7, 8 lần lượt là $x, y, z$ quyển (x, y, z ∈ ℕ*).
Do số vở quyên góp được của ba khối tỉ lệ thuận với $8, 7, 6$ nên:
$\dfrac{x}{8} = \dfrac{y}{7} = \dfrac{z}{6}$
Do số vở khối 8 quyên góp được ít hơn số vở khối 6 quyên góp được là $80$ quyển nên $x – z = 80$.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
$\dfrac{x}{8} = \dfrac{y}{7} = \dfrac{z}{6} = \dfrac{x – z}{8 – 6} = \dfrac{80}{2} = 40$
Khi đó $⇒ x = 8 . 40 = 320$, $y = 7 . 40 = 280$, $z = 6 . 40 = 240$
Vậy số vở quyên góp được của ba khối $6, 7, 8$ lần lượt là $320$ quyển, $280$ quyển, $240$ quyển.
Giải bài 6 trang 110 Toán 7 tập 2 KNTT
Cho hai đa thức $A = 6x^3 – 4x^2 – 12x – 7$ và $B = 2x^2 – 7$.
a) Xác định hệ số cao nhất và hệ số tự do trong mỗi đa thức đã cho.
b) Tính giá trị của đa thức $A + B$ tại $x = –2$.
c) Chứng minh rằng $x = 0, x = –1$ và $x = 2$ là ba nghiệm của đa thức $A – B$.
d) Thực hiện phép nhân $A . B$ bằng hai cách.
e) Tìm đa thức $R$ có bậc nhỏ hơn $2$ sao cho hiệu $A – R$ chia hết cho $B$.
Bài giải:
a) ♦ Xét đa thức $A = 6x^3 – 4x^2 – 12x – 7$
Đa thức $A$ có hạng tử có bậc cao nhất là $6x^3$ nên hệ số cao nhất là $6$.
Hạng tử có bậc bằng $0$ trong đa thức $A$ là $–7$ nên hệ số tự do là $–7$.
♦ Xét đa thức $B = 2x^2 – 7$
Đa thức $B$ có hạng tử có bậc cao nhất là $2x^2$ nên hệ số cao nhất là $2$.
Hạng tử có bậc bằng $0$ trong đa thức $B$ là $–7$ nên hệ số tự do là $–7$.
b) Ta có:
$A + B = 6x^3 – 4x^2 – 12x – 7 + 2x^2 – 7$
$= 6x^3 + (-4x^2 + 2x^2) – 12x + (-7 – 7)$
$= 6x^3 – 2x^2 – 12x – 14$
Thay $x = -2$ vào đa thức $A + B$ ta được:
$A + B = 6 . (-2)^3 – 2 . (-2)^2 – 12 . (-2) – 14$
$= 6 . (-8) – 2.4 – (-24) – 14$
$= -48 – 8 + 24 – 14$
$= -46$
Vậy $A + B = -46$ tại $x = -2$.
c) Ta có:
$A – B = (6x^3 – 4x^2 – 12x – 7) – (2x^2 – 7)$
$= 6x^3 – 4x^2 – 12x – 7 – 2x^2 + 7$
$= 6x^3 + (-4x^2 – 2x^2) – 12x + (-7 + 7)$
$= 6x^3 – 6x^2 – 12x$
♦ Tại $x = 0$ thì:
$A – B = 6 . 0^3 – 6 . 0^2 – 12 . 0 = 0$
♦ Tại $x = -1$ thì:
$A – B = 6 . (-1)^3 – 6 . (-1)^2 – 12 . (-1) = -6 – 6 + 12 = 0$
♦ Tại $x = 2$ thì:
$A – B = 6.2^3 – 6.2^2 – 12.2 = 6.8 – 6.4 – 24 = 0$
Vậy $x = 0, x = -1$ và $x = 2$ là ba nghiệm của đa thức $A – B$.
d) ♦ Cách 1. Bỏ dấu ngoặc:
$A . B = (6x^3 – 4x^2 – 12x – 7) . (2x^2 – 7)$
$= [6x^3 + (-4x^2) + (-12x) + (-7)] . [2x^2 + (-7)]$
$= 6x^3 . 2x^2 + 6x^3 . (-7) + (-4x^2) . 2x^2 + (-4x^2) . (-7)\\+ (-12x) . 2x^2 + (-12x) . (-7) + (-7) . 2x^2 + (-7) . (-7)$
$= 12x^5 + (-42 x^3) + (-8 x^4) + 28x^2 + (-24x^3) + 84x + (-14x^2) + 49$
$= 12x^5 – 8x^4 + (-42 x^3 – 24x^3) + (28x^2 – 14x^2) + 84x + 49$
$= 12x^5 – 8x^4 – 66x^3 + 14x^2 + 84x + 49$
♦ Cách 2. Đặt phép tính:
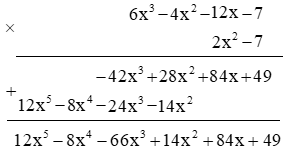
Vậy $A . B = 12x^5 – 8x^4 – 66x^3 + 14x^2 + 84x + 49$
e) Đặt phép chia $A$ cho $B$ ta được:
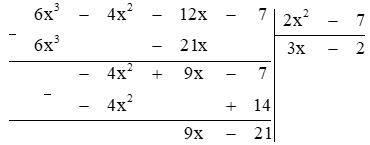
Đa thức $A$ chia cho đa thức $B$ dư $9x – 21$
Do đó để $A – R$ chia hết cho $B$ và bậc của đa thức $R$ nhỏ hơn $2$ thì đa thức $R$ bằng $9x – 21$.
Giải bài 7 trang 110 Toán 7 tập 2 KNTT
Người ta đổ đầy nước vào một cái bể hình hộp chữ nhật, sau đó nhấn chìm một khối lập phương (đặc) có độ dài các cạnh bằng $x$ (dm) vào trong bể. Biết rằng chiều rộng, chiều dài và chiều cao của bể lần lượt bằng $x + 1, x + 3$ và $x + 2$ (xem hình bên).
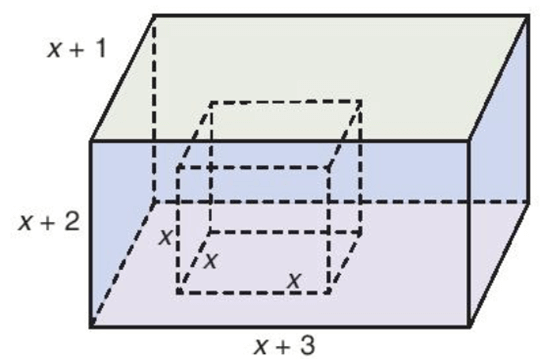
a) Tìm đa thức biểu thị thể tích nước còn lại trong bể.
b) Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức trong câu a.
c) Sử dụng kết quả câu a để tính lượng nước còn lại trong bể (đơn vị: $dm^3$) khi $x = 7 \,dm$.
Bài giải:
Do bể đầy nước nên khi thả khối lập phương vào thì lượng nước trào ra ngoài bằng thể tích của khối lập phương.
a) Thể tích của bể là:
$(x + 1)(x + 3)(x + 2) \,(dm^3)$
Thể tích khối gỗ là: $x^3 \,(dm^3)$
Thể tích nước còn lại trong bể là:
$(x + 1)(x + 3)(x + 2) – x^3$
$= (x.x + x.3 + 1.x + 1.3)(x + 2) – x^3$
$= (x^2 + 4x + 3)(x + 2) – x^3$
$= (x^2.x + x^2.2 + 4x.x + 4x.2 + 3.x + 3.2) – x^3$
$= x^3 + 2x^2 + 4x^2 + 8x + 3x + 6 – x^3$
$= (x^3 – x^3) + (2x^2 + 4x^2) + (8x + 3x) + 6$
$= 6x^2 + 11x + 6$
Vậy thể tích nước còn lại trong bể bằng $6x^2 + 11x + 6 \,(dm^3)$.
b) Đa thức $6x^2 + 11x + 6$ có hạng tử có bậc cao nhất là $6x^2$ nên bậc của đa thức đó bằng $2$, hệ số cao nhất bằng $6$.
Hạng tử có bậc bằng $0$ trong đa thức đó bằng $6$ nên hệ số tự do bằng $6$.
c) Tại $x = 7 \,dm$, thể tích nước còn lại trong bể bằng:
$6 . 7^2 + 11 . 6 + 6 = 6 . 49 + 66 + 6 = 366 \,(dm^3)$.
HÌNH HỌC VÀ ĐO LƯỜNG
Giải bài 8 trang 111 Toán 7 tập 2 KNTT
Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho $DM = DC$.
a) Chứng minh rằng $∆ADM = ∆BDC$. Từ đó suy ra $AM = BC$ và $AM // BC$.
b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho $EN = EB$. Chứng minh rằng $AN // BC$.
c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.
Bài giải:
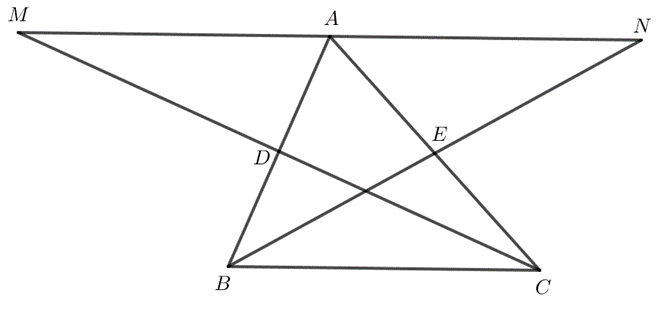
a) Do $D$ là trung điểm của $AB$ nên $AD = BD$
Xét $∆ADM$ và $∆BDC$ có:
$AD = BD$ (chứng minh trên)
$\widehat {ADM} = \widehat {BDC}$ (2 góc đối đỉnh)
$DM = DC$ (theo giả thiết)
Suy ra $∆ADM = ∆BDC$ (c.g.c)
Do đó $AM = BC$ (2 cạnh tương ứng) và $\widehat {DAM} = \widehat {DBC}$ (2 góc tương ứng)
Mà hai góc này ở vị trí so le trong nên $AM // BC$.
b) Do $E$ là trung điểm của $AC$ nên $AE = CE$
Xét $∆AEN$ và $∆CEB$ có:
$AE = CE$ (chứng minh trên)
$\widehat {AEN} = \widehat {CEB}$ (2 góc đối đỉnh)
$EN = EB$ (theo giả thiết)
Suy ra $∆AEN = ∆CEB$ (c.g.c)
Do đó $AN = BC$ (2 cạnh tương ứng) và $\widehat {EAN} = \widehat {ECB}$ (2 góc tương ứng)
Mà hai góc này ở vị trí so le trong nên $AN // BC$.
c) Ta có $AM // BC, AN // BC$ mà $AM$ cắt $AN$ tại $A$ nên $M, A, N$ thẳng hàng và $A$ nằm giữa $M$ và $N$
Lại có $AM = AN$ nên $A$ là trung điểm của $MN$
Vậy ta có điều phải chứng minh.
Giải bài 9 trang 111 Toán 7 tập 2 KNTT
Cho tam giác cân ABC tại đỉnh A. Gọi H là trung điểm của BC.
a) Chứng minh $AH ⊥ BC$.
b) Trên tia đối của tia BC lấy điểm M; trên tia đối của tia CB lấy điểm N sao cho $BM = CN$. Chứng minh rằng $∆ABM = ∆ACN$.
c) Gọi I là điểm trên AM, K là điểm trên AN sao cho $BI ⊥ AM$; $CK ⊥ AN$. Chứng minh rằng tam giác AIK cân tại A, từ đó suy ra $IK // MN$.
Bài giải:
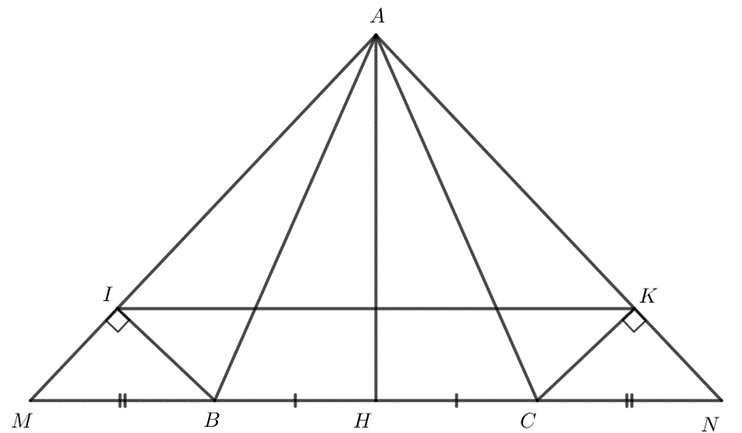
a) Do $H$ là trung điểm của $BC$ nên $BH = CH$.
Tam giác $ABC$ cân tại $A$ nên $AB = AC$ và $\widehat {ABC} = \widehat {ACB}$
Xét $∆ABH$ và $∆ACH$ có:
$AB = AC$ (chứng minh trên)
$BH$ chung
$BH = CH$ (chứng minh trên)
Suy ra $∆ABH = ∆ACH$ (c.g.c)
Do đó $\widehat {AHB} = \widehat {AHC}$ (2 góc tương ứng).
Mà $\widehat {AHB} = \widehat {AHC} = 180^o$ nên $\widehat {AHB} = \widehat {AHC} = 90^o$
Do đó $AH ⊥ BC$.
b) Ta có:
$\widehat {ABM}$ là góc ngoài tại đỉnh $B$ của $∆ABC$ nên $\widehat {ABM} = \widehat {BAC} + \widehat {ACB}$
$\widehat {ACN}$ là góc ngoài tại đỉnh $C$ của $∆ABC$ nên $\widehat {ACN} = \widehat {BAC} + \widehat {ABC}$
Mà $\widehat {ABC} = \widehat {ACB}$ nên $\widehat {ABM} = \widehat {ACN}$
Xét $∆ABM$ và $∆ACN$ có:
$AB = AC$ (chứng minh trên)
$\widehat {ABM} = \widehat {ACN}$ (chứng minh trên)
$BM = CN$ (theo giả thiết)
Suy ra $∆ABM = ∆ACN$ (c.g.c)
c) Do $∆ABM$ = $∆ACN$ (c.g.c) nên $\widehat {BAM} = \widehat {CAN}$ (2 góc tương ứng)
Xét $∆BAI$ vuông tại $I$ và $∆CAK$ vuông tại $A$:
$\widehat {BAI} = \widehat {CAK}$ (chứng minh trên)
$AB = AC$ (chứng minh trên)
Suy ra $∆BAI = ∆CAK$ (cạnh huyền – góc nhọn)
Do đó $AI = AK$ (2 cạnh tương ứng)
Xét $∆AIK$ có $AI = AK$ nên $∆AIK$ cân tại $A$
Ta có: $∆ABM = ∆ACN$ nên $AM = AN$ (2 cạnh tương ứng)
Xét ∆ABM có $AM = AN$ nên $∆AMN$ cân tại $A$
Do ∆AMN cân tại A nên $\widehat {AMN} = \widehat {ANM}$
Lại có: $\widehat {AMN} + \widehat {ANM} + \widehat {MAN} = 180^o$
Suy ra $2\widehat {AMN} + \widehat {MAN} = 180^o$
Do đó $\widehat {AMN} = \dfrac{180^o – \widehat {MAN}}{2}$ (1)
Do $∆AIK$ cân tại $A$ nên $\widehat {AIK} = \widehat {AKI}$
Lại có: $\widehat {AIK} + \widehat {AKI} + \widehat {IAK} = 180^o$
Suy ra $2\widehat {AIK} + \widehat {IAK} = 180^o$
Do đó $\widehat {AIK} = \dfrac{180^o – \widehat {IAK}}{2}$ (2)
Từ (1) và (2) suy ra $\widehat {AIK} = \widehat {AMN}$
Mà hai góc này ở vị trí đồng vị nên $IK // MN$
Vậy ta có điều phải chứng minh.
Giải bài 10 trang 111 Toán 7 tập 2 KNTT
Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho $BD = BA$ và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt tia BA tại M. Chứng minh rằng:
a) $∆ABH = ∆DBH$;
b) Tam giác AED cân;
c) $EM > ED$;
d) Tam giác BCM là tam giác đều và $CE = 2EA$ biết \(\widehat {ABC} = 60^o\).
Bài giải:
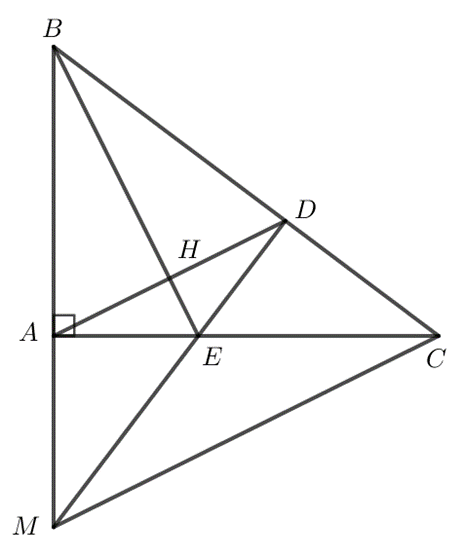
a) Do $H$ là trung điểm của $AD$ nên $AH = DH$
Xét $∆ABH$ và $∆DBH$ có:
$AB = DB$ (theo giả thiết)
$BH$ chung
$AH = DH$ (chứng minh trên)
Suy ra $∆ABH = ∆DBH$ (c.c.c)
b) Do $∆ABH = ∆DBH$ (c.c.c) nên $\widehat {ABH} = \widehat {DBH}$ (2 góc tương ứng)
Xét $∆ABE$ và $∆DBE$ có:
$AB = DB$ (theo giả thiết)
$\widehat {ABE} = \widehat {DBE}$ (chứng minh trên)
$BE$ chung
Suy ra $∆ABE = ∆DBE$ (c.g.c)
Do đó $AE = DE$ (2 cạnh tương ứng)
Xét $∆AED$ có $AE = DE$ nên $∆AED$ cân tại $E$.
c) Xét $∆AME$ vuông tại $A$ có $EM$ là cạnh huyền nên $EM$ là cạnh lớn nhất trong tam giác
Do đó $EM > EA$
Mà $EA = ED$ nên $EM > ED$.
d) Do $∆AME = ∆DBE$ (c.g.c) nên $\widehat {BAE} = \widehat {BDE} = 90^o$
Do đó $ED ⊥ BC$ hay $MD ⊥ BC$.
Xét $∆BCM$ có $CA ⊥ BM, MD ⊥ BC$
Mà $CA$ cắt $MD$ tại $E$ nên $E$ là trực tâm của $∆BCM$.
Khi đó $BE ⊥ MC$
Ta có $\widehat {ABE} = \widehat {DBE}$ nên $BE$ là tia phân giác của $\widehat {MBC}$
$∆BCM$ có $BE$ vừa là đường cao, vừa là tia phân giác nên $∆BCM$ cân tại $B$
Khi đó nếu $\widehat {ABC} = 60^o$ thì cân tại $B$, có $\widehat {MBC} = 60^o$ nên là tam giác đều.
⇒ $E$ vừa là trực tâm, vừa là trọng tâm của $∆BCM$
Do đó $CE = 2EA$.
THỐNG KÊ VÀ XÁC SUẤT
Giải bài 11 trang 111 Toán 7 tập 2 KNTT
Bình thu thập số liệu về số học sinh phổ thông của cả nước từ năm 2015 đến năm 2020 và vẽ được biểu đồ sau:
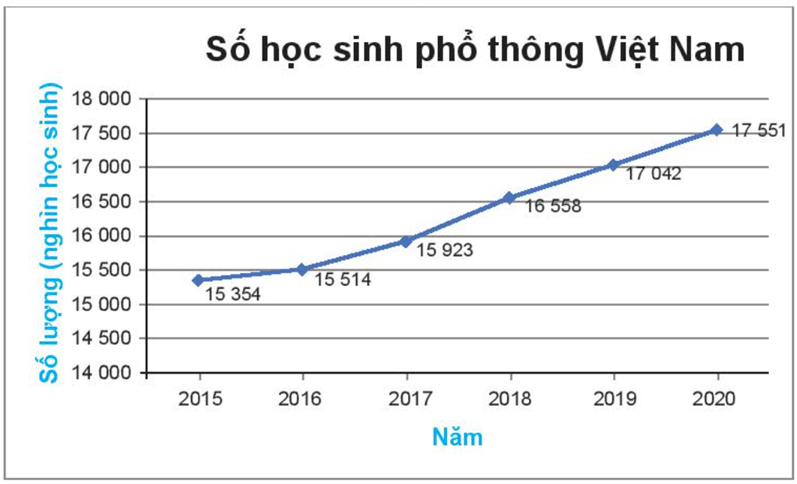
a) Số học sinh phổ thông cả nước từ năm 2015 đến năm 2020 có xu thế tăng hay giảm?
b) Hãy lập bảng thống kê về số lượng học sinh phổ thông của cả nước từ năm 2015 đến năm 2020.
c) Theo em, Bình đã dùng cách nào trong các cách thu thập dữ liệu đã học để có được số liệu trên?
Bài giải:
a) Số học sinh phổ thông cả nước từ năm 2015 đến năm 2020 có xu thế tăng.
b) Bảng thống kê số học sinh phổ thông cả nước từ năm 2015 đến năm 2020:
| Năm | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
| Số lượng (nghìn học sinh) | 15 354 | 15 514 | 15 923 | 16 558 | 17 042 | 17 551 |
c) Bình đã sử dụng phương pháp thu thập số liệu từ nguồn internet.
Giải bài 12 trang 112 Toán 7 tập 2 KNTT
Biểu đồ nào sau đây cho biết tổng số huy chương thế giới mà thể thao Việt Nam giành được trong các năm từ 2015 đến 2019:
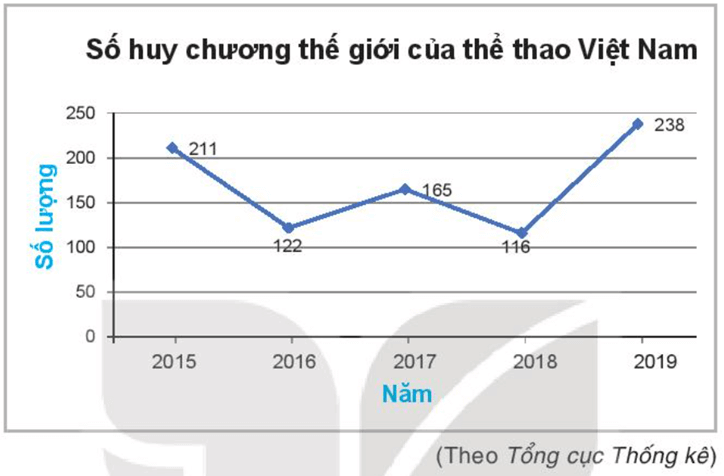
a) Lập bảng thống kê về số huy chương thế giới mà thể thao Việt Nam đạt được từ năm 2015 đến năm 2019.
b) Trong các năm trên, năm nào thể thao Việt Nam giành được ít huy chương thế giới nhất?
c) Tỉ lệ các loại huy chương thế giới của thể thao Việt Nam trong năm 2019 được cho trong biểu đồ sau:
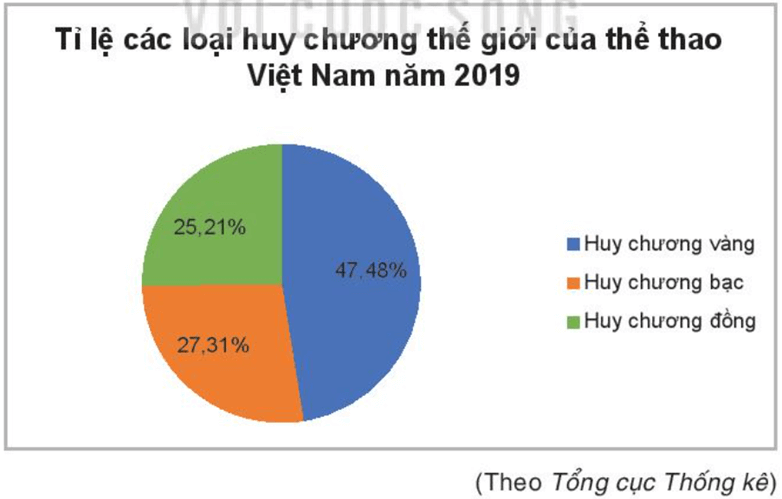
Tính số lượng mỗi loại huy chương thế giới mà thể thao Việt Nam giành được trong năm 2019.
Bài giải:
a) Bảng thống kê về số huy chương thế giới thể thao Việt Nam đạt được từ năm 2015 đến năm 2019:
| Năm | 2015 | 2016 | 2017 | 2018 | 2019 |
| Số lượng | 211 | 122 | 165 | 116 | 238 |
b) Năm 2018 là năm thể thao Việt Nam giành được ít huy chương thế giới nhất.
c) Số huy chương vàng đạt được trong năm 2019 là:
$238 . 47,48\% = 113,0024 ≈ 113$ (chiếc)
Số huy chương bạc đạt được trong năm 2019 là:
$238 . 27,31\% = 64,9978 ≈ 65$ (chiếc)
Số huy chương đồng đạt được trong năm 2019 là:
$238 – 113 – 65 = 60$ (chiếc).
Giải bài 13 trang 113 Toán 7 tập 2 KNTT
Trong trò chơi Vòng quay may mắn, người chơi sẽ quay một bánh xe hình tròn. Bánh xe được chia làm 12 hình quạt bằng nhau như hình bên. Trong mỗi hình quạt có ghi số điểm mà người chơi sẽ nhận được. Có hai hình quạt ghi 100 điểm; hai hình quạt ghi 200 điểm; hai hình quạt ghi 300 điểm; hai hình quạt ghi 400 điểm; một hình quạt ghi 500 điểm; hai hình quạt ghi 1 000 điểm và một hình quạt ghi 2 000 điểm. Khi bánh xe dừng lại, mũi tên (đặt cố định ở phía trên) chỉ vào hình quạt nào thì người chơi nhận được số điểm ghi trong hình quạt đó.
Bạn Mai tham gia trò chơi và quay một lần. Tính xác suất để mũi tên chỉ vào hình quạt:
a) Có số điểm nhỏ hơn 2 000;
b) Có số điểm nhỏ hơn 100;
c) Có số điểm lớn hơn 300;
d) Có số điểm là 2 000.
Bài giải:
a) Có $1$ hình quạt trong $12$ hình quạt có số điểm $2 \,000$ nên có $11$ hình quạt có số điểm nhỏ hơn $2 \,000$.
Do đó xác suất để mũi tên chỉ vào hình quạt có số điểm nhỏ hơn $2 \,000$ là: $\dfrac{11}{12}$.
b) Không có hình quạt nào có số điểm nhỏ hơn $100$ nên xác suất để mũi tên chỉ vào hình quạt có số điểm nhỏ hơn $100$ là $0$.
c) Có $6$ hình quạt trong $12$ hình quạt có số điểm lớn hơn $300$ nên xác xuất để mũi tên chỉ vào hình quạt có số điểm lớn hơn $300$ là $\dfrac{6}{12} = \dfrac{1}{2}$.
d) Có $1$ hình quạt trong $12$ hình quạt có số điểm $2 \,000$ nên xác suất để mũi tên chỉ vào hình quạt có số điểm bằng $2 \,000$ là: $\dfrac{1}{12}$.
Bài trước:
👉 HĐTH&TN: Hộp quà và chân đế lịch để bàn của em Toán 7 tập 2 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải Bài tập ôn tập cuối năm sgk Toán 7 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
