Nội Dung
Hướng dẫn giải Bài tập cuối chương 7 sgk Toán 7 tập 2 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 42 sgk Toán 7 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
GIẢI BÀI TẬP CUỐI CHƯƠNG 7
Sau đây là phần Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 42 sgk Toán 7 tập 2 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 42 Toán 7 tập 2 CTST
Cho \(A = {x^2}y + 2xy – 3{y^2} + 4\). Tính giá trị của biểu thức $A$ khi $x = -2, y = 3$.
Bài giải:
Ta có:
\(A = {x^2}y + 2xy – 3{y^2} + 4\)
Thay $x = -2$ và $y = 3$ vào công thức trên ta được:
$A = {(- 2)^2}.3 + 2( – 2).3 – {3.3^2} + 4$
$= 4.3 – 12 – 27 + 4$
$= – 23$
Vậy $A = -23$ khi $x = -2, y = 3$.
Giải bài 2 trang 42 Toán 7 tập 2 CTST
Trong các biểu thức sau, biểu thức nào là đơn thức một biến?
a) $2y$;
b) $3x + 5$;
c) $8$;
d) \(21t^{12}\).
Bài giải:
Các đa thức một biến là a), c), d).
Giải bài 3 trang 42 Toán 7 tập 2 CTST
Trong các biểu thức sau, biểu thức nào là đa thức một biến?
\(3 + 6y\);
\(7x^2 + 2x – 4x^4 + 1\);
\(\dfrac{2}{x + 1}\);
\(\dfrac{1}{3}x – 5\).
Bài giải:
Các đa thức một biến là:
\(3 + 6y; 7x^2 + 2x – 4x^4 + 1; \dfrac{1}{3}x – 5\).
Giải bài 4 trang 42 Toán 7 tập 2 CTST
Hãy viết một đa thức một biến bậc ba có 3 số hạng.
Bài giải:
Ví dụ: đa thức một biến bậc ba có 3 số hạng
\(x^3 + 2x – 1\) hoặc $x^3 + 3x^2 + 1$.
Chú ý: Có nhiều cách khác nhau để viết đa thức nhưng trong bài này các số hạng trong đa thức luôn luôn là 3.
Giải bài 5 trang 42 Toán 7 tập 2 CTST
Hãy cho biết bậc của các đa thức sau:
\(A = 3x – 4x^2 + 1\);
\(B = 7\);
\(M = x – 7{x^3} + 10{x^4} + 2\).
Bài giải:
Đa thức $A$ có hạng tử bậc cao nhất là $-4x^2$ nên bậc của đa thức $A$ là $2$.
$7$ có bậc bằng $0$ nên bậc của đa thức $B$ là $0$.
Đa thức $M$ có hạng tử bậc cao nhất là $10x^4$ nên bậc của đa thức $M$ là $4$.
Giải bài 6 trang 42 Toán 7 tập 2 CTST
Cho đa thức \(P(x) = x^3 + 27\). Tìm nghiệm của $P(x)$ trong tập hợp \(\left\{ {0;3; – 3} \right\}\).
Bài giải:
Xét đa thức:
\(P(x) = x^3 + 27 = 0\)
$⇔ x^3 = – 27$
$⇔ x^3 = (- 3)^3$
$⇒ x = – 3$
Vì \(- 3 \in \left\{ {0;3; – 3} \right\}\) nên $-3$ là $1$ nghiệm của đa thức $P(x)$.
Giải bài 7 trang 42 Toán 7 tập 2 CTST
Tam giác trong Hình 1 có chu vi bằng $(25y – 8) \,cm$. Tìm cạnh chưa biết trong tam giác đó.
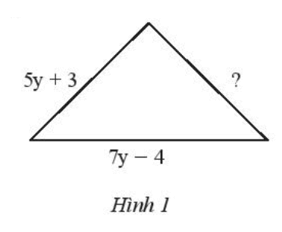
Bài giải:
Cạnh còn lại cần tìm của tam giác là:
$25y – 8 – (5y + 3) – (7y – 4)$
$= 25y -8- 5y – 3-7y+4$
$=(25y-5y-7y) +(-8-3+4)$
$= 13y – 7 \,(cm)$
Vậy độ dài cạnh còn lại trong tam giác đó là $13y – 7 \,(cm)$.
Giải bài 8 trang 42 Toán 7 tập 2 CTST
Cho đa thức \(M(x) = 2{x^4} – 5{x^3} + 7{x^2} + 3x\).
Tìm các đa thức $N(x), Q(x)$ sao cho: \(N(x) – M(x) = – 4{x^4} – 2{x^3} + 6{x^2} + 7\) và \(M(x) + Q(x) = 6{x^5} – {x^4} + 3{x^2} – 2\).
Bài giải:
♦ Theo đề bài ta có:
\(M(x) = 2{x^4} – 5{x^3} + 7{x^2} + 3x\)
$M(x) + Q(x) = 6{x^5} – {x^4} + 3{x^2} – 2$
$⇒ Q(x) = (6{x^5} – {x^4} + 3{x^2} – 2) – (2{x^4} – 5{x^3} + 7{x^2} + 3x)$
$= 6{x^5} – {x^4} + 3{x^2} – 2 – 2{x^4} + 5{x^3} – 7{x^2} – 3x$
$= 6{x^5} – 3{x^4} + 5{x^3} – 4{x^2} – 3x – 2$
Vậy $Q(x) = 6{x^5} – 3{x^4} + 5{x^3} – 4{x^2} – 3x – 2$.
♦ Theo đề bài ta có:
$N(x) – M(x) = – 4{x^4} – 2{x^3} + 6{x^2} + 7$
$⇒ N(x) = – 4{x^4} – 2{x^3} + 6{x^2} + 7 + 2{x^4} – 5{x^3} + 7{x^2} + 3x$
$= – 2{x^4} – 7{x^3} + 13{x^2} + 3x + 7$
Vậy $N(x) = – 2{x^4} – 7{x^3} + 13{x^2} + 3x + 7$.
Giải bài 9 trang 42 Toán 7 tập 2 CTST
Thực hiện phép nhân.
a) \((3x – 2)(4x + 5)\);
b) \(({x^2} – 5x + 4)(6x + 1)\).
Bài giải:
a) Ta có:
\((3x – 2)(4x + 5)\)
$= 3x(4x + 5) – 2(4x + 5)$
$= 3x.4x + 5.3x – 2.4x – 2.5$
$= 12{x^2} + 7x – 10$
Vậy \((3x – 2)(4x + 5) = 12{x^2} + 7x – 10\).
b) Ta có:
\(({x^2} – 5x + 4)(6x + 1)\)
$= {x^2}(6x + 1) – 5x(6x + 1) + 4(6x + 1)$
$= {x^2}.6x + 1.{x^2} – 5x.6x – 5x.1 + 4.6x + 4.1$
$= 6{x^3} – 29{x^2} + 19x + 4$
Vậy \(({x^2} – 5x + 4)(6x + 1) = 6{x^3} – 29{x^2} + 19x + 4\).
Giải bài 10 trang 42 Toán 7 tập 2 CTST
Thực hiện phép chia.
a) \((45{x^5} – 5{x^4} + 10{x^2}):5{x^2}\);
b) \((9{t^2} – 3{t^4} + 27{t^5}):3t\).
Bài giải:
a) Ta có:
\((45{x^5} – 5{x^4} + 10{x^2}):5{x^2}\)
$= (45x^5 : 5x^2) + (-5x^4 : 5x^2) + (10x^2 : 5x^2)$
\(= 9{x^3} – {x^2} + 2\)
Vậy \((45{x^5} – 5{x^4} + 10{x^2}):5{x^2} = 9{x^3} – {x^2} + 2\).
b) Ta có:
$(9{t^2} – 3{t^4} + 27{t^5}):3t$
$= (27{t^5} – 3{t^4} + 9{t^2}):3t$
$=(27t^5):(3t) – (3t^4):(3t)+(9t^2):(3t)$
$= 9{t^4} – 3{t^3} + 3t$
Vậy \((9t^2 – 3t^4 + 27t^5):3t = 9t^4 – 3t^3 + 3t\).
Giải bài 11 trang 42 Toán 7 tập 2 CTST
Thực hiện phép chia.
a) \((2y^4 – 13y^3 + 15y^2 + 11y – 3):(y^2 – 4y – 3)\);
b) \((5x^3 – 3x^2 + 10):(x^2 + 1)\).
Bài giải:
a) Thực hiện đặt phép chia ta được:

Vậy $2y^4 – 13y^3 + 15y^2 + 11y – 3) : (y^2 – 4y – 3) = 2y^2 – 5y + 1$.
b) Thực hiện đặt phép chia ta được:

Vậy \((5x^3 – 3x^2 + 10):(x^2 + 1) = 5x-3+\dfrac{-5x+13}{x^2+1}\).
Hay \((5x^3 – 3x^2 + 10) = (5x – 3).(x^2 + 1) – 5x + 13\).
Bài trước:
👉 HĐTH&TN: Cách tính điểm trung bình môn học kì Toán 7 tập 2 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 trang 46 47 sgk Toán 7 tập 2 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 42 sgk Toán 7 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
