Giải bài 1 2 3 4 5 6 7 8 9 10 trang 26 27 sgk Toán 8 tập 2 Chân Trời Sáng Tạo

Nội Dung

Hướng dẫn giải Bài 4. Hệ số góc của đường thẳng sgk Toán 8 tập 2 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 5 6 7 8 9 10 trang 26 27 sgk Toán 8 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.

BÀI 4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG

Hoạt động khởi động trang 23 Toán 8 tập 2 CTST

Khi nào thì hai đường thẳng $y = ax + b(a \ne 0)$ và $y = a’x + b'(a’ \ne 0)$ song song với nhau, trùng nhau, cắt nhau?

Trả lời:

– Hai đường thẳng $y = ax + b(a \ne 0)$ và $y = a’x + b'(a’ \ne 0)$ song song với nhau khi $a = a’$ và $b ≠ b’$.

– Hai đường thẳng $y = ax + b(a \ne 0)$ và $y = a’x + b'(a’ \ne 0)$ cắt nhau khi $a ≠ a’$.

– Hai đường thẳng $y = ax + b(a \ne 0)$ và $y = a’x + b'(a’ \ne 0)$ trùng nhau khi $a = a’$ và $b = b’$.

1. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG $y = ax + b (a≠0)$

Hoạt động khám phá 1 trang 23 Toán 8 tập 2 CTST

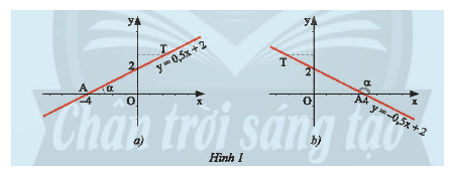
a) Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng $y = ax + b(a \ne 0)$ cắt $Ox$ tại điểm $A$ và $T$ là một điểm trên đường thẳng $y = ax + b(a \ne 0)$ có tung độ dương (Hình 1).

Ta gọi $\alpha = \widehat {xAT}$ là góc tạo bởi đường thẳng $y = ax + b(a \ne 0)$ và trục $Ox$.

Hãy nêu nhận xét của em về số đo của góc $\alpha $ và hệ số $a$ trong hai trường hợp dưới đây.

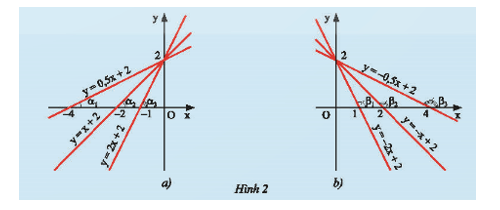
b) Hãy so sánh các hệ số $a$ của các đường thẳng $y = ax + b(a \ne 0)$ trong mỗi hình ở Hình 2 và so sánh các góc $\alpha $ hoặc các góc $\beta $ tạo bởi các đường thẳng đó với trục $Ox$.

Trả lời:

a) – Ở Hình 1a) là đồ thị của hàm số $y = 0,5x + 2$ hệ số $a = 0,5 > 0$;

Dùng thước đo độ kiểm tra ta thấy góc $\alpha $ là góc nhọn.

– Ở Hình 1b) là đồ thị của hàm số $y = – 0,5x + 2$ hệ số $a = – 0,5 < 0$;

Dùng thước đo độ kiểm tra ta thấy góc $\alpha $ là góc tù.

b) – Ở Hình 2a) là đồ thị của 3 hàm số $y = 0,5x + 2;y = x + 2;y = 2x + 2$.

Ta có: ${a_1} = 0,5;{a_2} = 1;{a_3} = 2$ nên ${a_1} < {a_2} < {a_3}$.

Ta có: ${\alpha _1} < {\alpha _2}$ (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

${\alpha _2} < {\alpha _3}$ (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

Do đó, ${\alpha _1} < {\alpha _2} < {\alpha _3}$.

– Ở Hình 2b) là đồ thị của 3 hàm số $y = – 2x + 2;y = – x + 2;y = – 0,5x + 2$.

Ta có: ${a_1} = – 2;{a_2} = – 1;{a_3} = – 0,5$ nên ${a_1} < {a_2} < {a_3}$.

Ta có: ${\beta _1} < {\beta _2}$ (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

${\beta _2} < {\beta _3}$ (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

Do đó, ${\beta _1} < {\beta _2} < {\beta _3}$.

Kết luận:

• Với hệ số $a$ dương, hệ số $a$ càng lớn thì góc $α$ càng lớn.

• Với hế số $a$ âm, hệ số $a$ càng lớn thì góc $β$ càng lớn.

Thực hành 1 trang 24 Toán 8 tập 2 CTST

Tìm hệ số góc của các đường thẳng sau đây:

a) $y = – 5x – 5$;

b) $y = \sqrt 3 x + 3$;

c) $y = \sqrt {11} x + \sqrt 7 $.

Trả lời:

a) Đường thẳng $y = – 5x – 5$ có hệ số góc là $a = – 5$.

b) Đường thẳng $y = \sqrt 3 x + 3$ có hệ số góc là $a = \sqrt 3 $.

c) Đường thẳng $y = \sqrt {11} x + \sqrt 7 $ có hệ số góc là $a = \sqrt {11} $.

Vận dụng 1 trang 24 Toán 8 tập 2 CTST

Trong các đường thẳng sau, đường thẳng nào tạo với $Ox$ một góc nhọn, đường thẳng nào tạo với $Ox$ một góc tù?

a) $y = 3x + 6$;

b) $y = – 4x + 1$;

c) $y = – 3x – 6$.

Trả lời:

a) Đường thẳng $y = 3x + 6$ có hệ số góc là $a = 3 > 0$ nên góc tạo bởi đường thẳng và trục $Ox$ là góc nhọn.

b) Đường thẳng $y = – 4x + 1$ có hệ số góc là $a = – 4 < 0$ nên góc tạo bởi đường thẳng và trục $Ox$ là tù.

c) Đường thẳng $y = – 3x – 6$ có hệ số góc là $a = – 3 < 0$ nên góc tạo bởi đường thẳng và trục $Ox$ là tù.

2. HAI ĐƯỜNG THẲNG SONG SONG, HAI ĐƯỜNG THẲNG CẮT NHAU

Hoạt động khám phá 2 trang 24 Toán 8 tập 2 CTST

Quan sát Hình 3.

a) So sánh hệ số góc của hai đường thẳng:

$d:y = 2x + 3$ và $d’:y = 2x – 2$.

Nêu nhận xét về vị trí giữa hai đường thẳng này.

b) Tìm đường thẳng $d”$ đi qua gốc tọa độ $O$ và song song với đường thẳng $d$.

Trả lời:

a) Đường thẳng $d:y = 2x + 3$ có hệ số góc là $a = 2$.

Đường thẳng $d’:y = 2x – 2$ có hệ số góc là $a’ = 2$.

Hệ số góc của hai đường thẳng $d$ và $d’$ bằng nhau.

Từ đồ thị ta thấy, hai đường thẳng $d$ và $d’$ song song với nhau.

b) Đường thẳng $d”$ đi qua gốc tọa độ $O$ nên có dạng $y = a”x$.

Từ đồ thị ta thấy, $d”$ đi qua điểm $(1;2)$ nên ta có:

$2 = 1.a” ⇒ a” = 2$.

Do đó, đường thẳng $d”$ là $y = 2x$.

Hoạt động khám phá 3 trang 25 Toán 8 tập 2 CTST

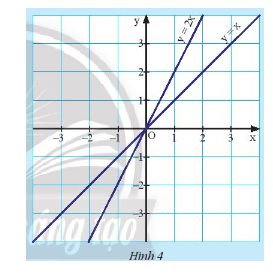
Quan sát Hình 4.

a) Tìm giao điểm của hai đường thẳng $d:y = 2x$ và $d’:y = x$.

b) Nêu nhận xét về hai đường thẳng có hệ số góc khác nhau.

c) Cho đường thẳng $d’:y = ax + b$ và cho biết $d”$ cắt $d$. Hệ số góc $a$ của đường thẳng $d”$ có thể nhận giá trị nào?

Trả lời:

a) Đường thẳng $d:y = 2x$ và $d’:y = x$ đều có dạng $y = ax$ nên giao điểm của hai đường thẳng là $O(0;0)$ (cả hai đường thẳng đều đi qua điểm $O(0;0)$.

b) – Hệ số góc của đường thẳng $d:y = 2x$ là $a = 2$.

– Hệ số góc của đường thẳng $d’:y = x$ là $a = 1$.

Hai đường thẳng có hệ số góc khác nhau thì cắt nhau.

c) Vì $d$ và $d”$ cắt nhau nên chúng không thể song song với nhau hoặc trùng nhau. Do đó, hệ số góc của $d$ và $d”$ phải khác nhau. Khi đó, hệ số góc của $d”$ khác $2$.

Thực hành 2 trang 26 Toán 8 tập 2 CTST

Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau:

${d_1}:y = 3x$;

${d_2}:y = – 7x + 9$;

${d_3}:y = 3x – 0,8$;

${d_4}:y = – 7x – 1$;

${d_5}:y = \sqrt 2 x + 10$;

${d_6}:y = \sqrt 2 x + \sqrt {10} $

Trả lời:

Ta có:

Hệ số góc của đường thẳng ${d_1}:y = 3x$ là $a = 3$;

Hệ số góc của đường thẳng ${d_2}:y = – 7x + 9$ là $a = – 7$;

Hệ số góc của đường thẳng ${d_3}:y = 3x – 0,8$ là $a = 3$;

Hệ số góc của đường thẳng ${d_4}:y = – 7x – 1$ là $a = – 7$;

Hệ số góc của đường thẳng ${d_5}:y = \sqrt 2 x + 10$ là $a = \sqrt 2 $;

Hệ số góc của đường thẳng ${d_6}:y = \sqrt 2 x + \sqrt {10} $ là $a = \sqrt 2 $;

– Ba cặp đường thẳng cắt nhau là:

${d_1}:y = 3x$ và ${d_4}:y = – 7x – 1$ vì có hệ số góc khác nhau $(3 \ne – 7)$.

${d_2}:y = – 7x + 9$ và ${d_6}:y = \sqrt 2 x + \sqrt {10} $ vì có hệ số góc khác nhau $( – 7 \ne \sqrt 2 )$.

${d_3}:y = 3x – 0,8$ và ${d_5}:y = \sqrt 2 x + 10$ vì có hệ số góc khác nhau $(3 \ne \sqrt 2 )$.

– Các cặp đường thẳng song song là:

♦ ${d_1}:y = 3x$ và ${d_3}:y = 3x – 0,8$ vì đều có hệ số góc $a = 3$ và chúng phân biệt với nhau do chúng cắt $Oy$ tại hai điểm phân biệt.

♦ ${d_2}:y = – 7x + 9$ và ${d_4}:y = – 7x – 1$ vì đều có hệ số góc $a = – 7$ và chúng phân biệt với nhau do chúng cắt $Oy$ tại hai điểm phân biệt.

♦ ${d_5}:y = \sqrt 2 x + 10$ và ${d_6}:y = \sqrt 2 x + \sqrt {10} $ vì đều có hệ số góc $a = \sqrt 2 $ và chúng phân biệt với nhau do chúng cắt $Oy$ tại hai điểm phân biệt.

Vận dụng 2 trang 26 Toán 8 tập 2 CTST

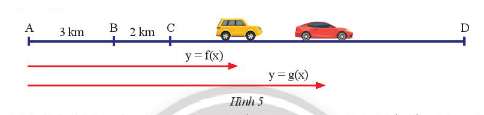
Hai ô tô khởi cùng lúc và cùng vận tốc $50 km/h$, một ô tô bắt đầu từ $B$, một ô tô bắt đầu từ $C$ và cùng đi về phía $D$.

a) Viết công thức của hai hàm số biểu thị khoảng cách từ $A$ đến mỗi xe sau $x$ giờ.

b) Chứng tỏ đồ thị của hai hàm số trên là hai đường thẳng song song.

Trả lời:

a) – Quãng đường xe ô tô khởi hành từ $B$ đi được sau khoảng thời gian $x(h)$ với vận tốc 50 km/h là: $s = v.t = 50.x$

Khi đó, công thức biểu thị khoảng cách từ điểm $A$ đến xe là:

$y = {y_0} + v.t = 3 + 50.x$.

– Quãng đường xe ô tô khởi hành từ $C$ đi được sau khoảng thời gian $x(h)$ với vận tốc 50 km/h là: $s = v.t = 50.x$

Khi đó, công thức biểu thị khoảng cách từ điểm $A$ đến xe là:

$y = {y_0} + v.t = 5 + 50.x$.

b) Đồ thị của hai hàm số trên là hai đường thẳng phân biệt vì cắt $Oy$ tại hai điểm phân biệt.

Hai đường thẳng đó song song với nhau vì hệ số góc của hai đường thẳng này bằng nhau (đều có $a = 50$).

GIẢI BÀI TẬP

Sau đây là phần Giải bài 1 2 3 4 5 6 7 8 9 10 trang 26 27 sgk Toán 8 tập 2 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 trang 26 Toán 8 tập 2 CTST

Cho hàm số bậc nhất $y = ax – 4$.

a) Tìm hệ số góc $a$ biết rằng đồ thị hàm số đi qua điểm $M(1; – 2)$.

b) Vẽ đồ thị của hàm số.

Bài giải:

a) Vì đồ thị hàm số đi qua điểm $M(1; – 2)$ nên ta có:

$ – 2 = a.1 – 4 \Leftrightarrow a = – 2 + 4 = 2$

Hàm số cần tìm là $y = 2x – 4$ có hệ số góc $a = 2$.

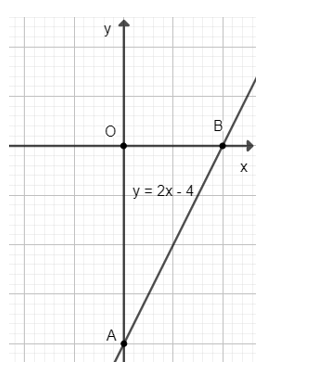
b) Cho $x = 0 ⇒ y = – 4$ ta được điểm $A(0; – 4)$ trên trục $Oy$.

Cho $y = 0 \Rightarrow x = \dfrac{4}{2} = 2$ ta được điểm $B(2;0)$ trên $Ox$.

Đồ thị hàm số là đường thẳng đi qua hai điểm $A$ và $B$.

Giải bài 2 trang 26 Toán 8 tập 2 CTST

a) Vẽ đồ thị của hàm số $y = x$ và $y = x + 2$ trên cùng một mặt phẳng tọa độ.

b) Dùng thước đo góc để tìm góc tạo bởi hai đường thẳng $y = x$ và $y = x + 2$ với trục $Ox$.

Bài giải:

a) – Vẽ đồ thị hàm số $d_2: y = x$.

Cho $x = 1 \Rightarrow y = 1 \Rightarrow $ Đồ thị hàm số đi qua điểm $(1;1)$.

Đồ thị hàm số $y = x$ là đường thẳng đi qua hai điểm $O$ và $M$.

– Vẽ đồ thị hàm số $d_1: y = x + 2$

Cho $x = 0 \Rightarrow y = 2$ ta được điểm $(0;2)$ trên trục $Oy$.

Cho $y = 0 \Rightarrow x = \dfrac{- 2}{1} = – 2$ ta được điểm $(- 2;0)$ trên $Ox$.

Đồ thị hàm số $y = x + 2$ là đường thẳng đi qua hai điểm $(- 2;0)$ và $(0;2)$.

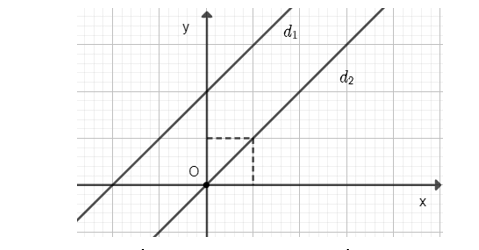
b) Góc tạo bởi hai đường thẳng $y = x$ và $y = x + 2$ với trục $Ox$ lần lượt là ${\alpha _1}$ và ${\alpha _2}$.

Dùng thước đo độ kiểm tra ta thấy số đo ${\alpha _1} = {\alpha _2} = 45^\circ $.

Giải bài 3 trang 26 Toán 8 tập 2 CTST

Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau:

${d_1}:y = 0,2x$;

${d_2}:y = – 2x + 4$;

${d_3}:y = 0,2x – 0,8$;

${d_4}:y = – 2x – 5$;

${d_5}:y = \sqrt 3 x + 3$;

${d_6}:y = \sqrt 3 x – \sqrt 5 $.

Bài giải:

Ta có:

Hệ số góc của đường thẳng ${d_1}:y = 0,2x$ là $a = 0,2$;

Hệ số góc của đường thẳng ${d_2}:y = – 2x + 4$ là $a = – 2$;

Hệ số góc của đường thẳng ${d_3}:y = 0,2x – 0,8$ là $a = 0,2$;

Hệ số góc của đường thẳng ${d_4}:y = – 2x – 5$ là $a = – 2$;

Hệ số góc của đường thẳng ${d_5}:y = \sqrt 3 x + 3$ là $a = \sqrt 3 $;

Hệ số góc của đường thẳng ${d_6}:y = \sqrt 3 x – \sqrt 5 $ là $a = \sqrt 3 $;

– Ba cặp đường thẳng cắt nhau là:

${d_1}:y = 0,2x$ và ${d_2}:y = – 2x + 4$ vì có hệ số góc khác nhau $(0,2 \ne – 2)$.

${d_3}:y = 0,2x – 0,8$ và ${d_4}:y = – 2x – 5$vì có hệ số góc khác nhau $(0,2 \ne – 2)$.

${d_5}:y = \sqrt 3 x + 3$ và ${d_4}:y = – 2x – 5$ vì có hệ số góc khác nhau $(\sqrt 3 \ne – 2)$.

– Các cặp đường thẳng song song là:

${d_1}:y = 0,2x$ và ${d_3}:y = 0,2x – 0,8$ vì đều có hệ số góc $a = 0,2$ và chúng phân biệt vì cắt $Oy$ tại hai điểm khác nhau.

${d_2}:y = – 2x + 4$ và ${d_4}:y = – 2x – 5$ vì đều có hệ số góc $a = – 2$và chúng phân biệt vì cắt $Oy$ tại hai điểm khác nhau.

${d_5}:y = \sqrt 3 x + 3$ và ${d_6}:y = \sqrt 3 x – \sqrt 5 $ vì đều có hệ số góc $a = \sqrt 3 $ và chúng phân biệt vì cắt $Oy$ tại hai điểm khác nhau.

Giải bài 4 trang 26 Toán 8 tập 2 CTST

Tìm hệ số góc $a$ để hai đường thẳng $y = ax + 2$ và $y = 9x – 9$ song song với nhau.

Bài giải:

Để hai đường thẳng $y = ax + 2$ và $y = 9x – 9$ song song với nhau thì:

$\left\{ \begin{array}{l}a = 9\\2 \ne – 9\end{array} \right. \Rightarrow a = 9$.

Do đó, để đường thẳng $y = ax + 2$ song song với đường thẳng $y = 9x – 9$ thì $a = 9$.

Giải bài 5 trang 26 Toán 8 tập 2 CTST

Cho hai hàm số bậc nhất $y = 2mx – 5$ và $y = 2x + 1$.

Với giá trị nào của $m$ thì đồ thị của hai hàm số đã cho là:

a) Hai đường thẳng song song với nhau?

b) Hai đường thẳng cắt nhau?

Bài giải:

a) Để đường thẳng $y = 2mx – 5$ và đường thẳng $y = 2x + 1$ song song với nhau thì:

$\left\{ \begin{array}{l}a = a’\\b \ne b’\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2m = 2\\ – 5 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 2:2\\ – 5 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\ – 5 \ne 1\end{array} \right.(tm)$

Vậy $m = 1$ thì hai đường thẳng $y = 2mx – 5$ và $y = 2x + 1$ song song với nhau.

b) Để đường thẳng $y = 2mx – 5$ và đường thẳng $y = 2x + 1$ cắt nhau thì:

$a \ne a’ \Rightarrow 2m \ne 2 \Leftrightarrow m \ne 2:2 \Leftrightarrow m \ne 1$.

Giải bài 6 trang 26 Toán 8 tập 2 CTST

Cho đường thẳng $d:y = x + 2023$. Xác định hai hàm số biết đồ thị của chúng là hai đường thẳng song song với $d$.

Bài giải:

Đường thẳng $d:y = x + 2023$ có $a = 1;b = 2023$.

– Gọi ${d_1}:y = {a_1}x + {b_1}$ là đường thẳng cần tìm thứ nhất. Vì ${d_1}$ song song với $d$ nên:

$\left\{ \begin{array}{l}a = {a_1}\\b \ne {b_1}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}1 = {a_1}\\2023 \ne {b_1}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{a_1} = 1\\{b_1} \ne 2023\end{array} \right.$.

Ta chọn ${b_1} = 25$,⇒ Ta có đường thẳng ${d_1}:y = x + 25$.

Vậy hàm số thứ nhất cần tìm là $y = x + 25$.

– Gọi ${d_2}:y = {a_2}x + {b_2}$ là đường thẳng cần tìm thứ hai. Vì ${d_2}$ song song với $d$ nên:

$\left\{ \begin{array}{l}a = {a_2}\\b \ne {b_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}1 = {a_2}\\2023 \ne {b_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{a_2} = 1\\{b_2} \ne 2023\end{array} \right.$.

Ta chọn ${b_2} = 5$,⇒ Ta có đường thẳng ${d_2}:y = x + 5$.

Vậy hàm số thứ hai cần tìm là $y = x + 5$.

Hoặc:

Đường thẳng song song với $d: y = x + 2023$ suy ra có hệ số góc bằng $1$.

Ví dụ:

Ta có: $d’: y = x – 23; \,d’’: y = x +1$.

Giải bài 7 trang 26 Toán 8 tập 2 CTST

Cho đường thẳng $d:y = – x – 2022$. Xác định hai hàm số biết đồ thị của chúng là hai đường thẳng cắt $d$.

Bài giải:

Đường thẳng $d:y = – x – 2022$ có $a = – 1;b = – 2022$.

– Gọi ${d_1}:y = {a_1}x + {b_1}$ là đường thẳng cần tìm thứ nhất.

Vì ${d_1}$ cắt $d$ nên $a \ne {a_1} \Rightarrow – 1 \ne {a_1}$ và ${b_1}$ tùy ý.

Ta chọn ${a_1} = 5;{b_1} = 4$,⇒ Ta có đường thẳng ${d_1}:y = 5x + 4$.

Vậy hàm số thứ nhất cần tìm là $y = 5x + 4$.

– Gọi ${d_2}:y = {a_2}x + {b_2}$ là đường thẳng cần tìm thứ hai.

Vì ${d_2}$ cắt $d$ nên $a \ne {a_2} \Rightarrow – 1 \ne {a_2}$ và ${b_2}$ tùy ý.

Ta chọn ${a_2} = 25;{b_2} = 5$,⇒ Ta có đường thẳng ${d_2}:y = 25x + 5$.

Vậy hàm số thứ hai cần tìm là $y = 25x + 5$.

Giải bài 8 trang 27 Toán 8 tập 2 CTST

Lam phụ giúp mẹ bánh nước chanh, em nhận thấy số ly nước chanh $y$ bán được trong ngày và nhiệt độ trung bình $x(^\circ C)$ của ngày hôm đó có mối tương quan. Lan ghi lại các giá trị tương ứng của hai đại lượng $x$ và $y$ trong bảng sau:

$x(^\circ C)$	20	22	24	26	28	30
$y$ (li nước chanh)	10	11	12	13	14	15

a) So sánh các giá trị $x$ và $y$ tương ứng trong bảng dữ liệu trên với tọa độ $(x;y)$ của các điểm $A;B;C;D;E;F$ trên mặt phẳng tọa độ trong Hình 6.

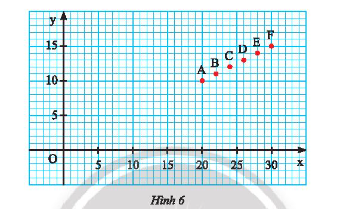
b) Cho biết đường thẳng $d:y = mx$ đi qua các điểm $A;B;C;D;E;F$ ở câu a. Tìm hệ số góc của $d$.

Bài giải:

a) Điểm $A(20;10);B(22;11);C(24;12);D(26;13);E(28;14);D(30;15)$

Ta thấy mỗi cặp giá trị $x;y$ tương ứng trong bảng là tọa độ của các điểm $A;B;C;D;E;F$.

b) Vì đường thẳng $d:y = mx$ đi qua các điểm $A;B;C;D;E;F$ nên ta chọn $A(20;10)$ thay vào đường thẳng ta được:

$10 = 20.m \Leftrightarrow m = 10:20 \Leftrightarrow m = \dfrac{1}{2}$

Do đó đường thẳng cần tìm là: $y = \dfrac{1}{2}x$.

Hệ số góc của đường thẳng là $a = \dfrac{1}{2}$.

Giải bài 9 trang 27 Toán 8 tập 2 CTST

Một xe khách khởi hành từ bến xe phía Nam bưu điện thành phố Huế để đi vào thành phố Quy Nhơn với tốc độ $50 km/h$.

a) Cho biết bến xe cách bưu điện thành phố Huế $4 km$. Sau $x$ giờ, xe khách cách bưu điện thành phố Huế $y km$. Tính $y$ theo $x$.

b) Tìm hệ số góc của đường thẳng là đồ thị của hàm số $y$ ở câu a.

Bài giải:

a) Quãng đường xe khách đi được sau $x$ giờ với vận tốc $50 km/h$ là: $50.x$ (km)

Vì ban đầu bến xe cách bưu điện thành phố Huế $4 km$ nên sau $x$ giờ xe khách cách bưu điện thành phố Huế số $km$ là: $50x + 4$.

Do đó, $y = 50x + 4$ với $y$ là số $km$ xe khách cách bưu điện thành phố Huế sau $x$ giờ.

b) Vì $y = 50x + 4$ là một hàm số bậc nhất nên hệ số góc của đường thẳng là độ thị của hàm số là: $a = 50$.

Giải bài 10 trang 27 Toán 8 tập 2 CTST

Một người bắt đầu mở một vòi nước vào một cái bể đã chứa sẵn $3 m^3$ nước, mỗi giờ chảy được $1 m^3$.

a) Tính thể tích $y({m^3})$ của nước có trong bể sau $x$ giờ.

b) Vẽ đồ thị của hàm số $y$ theo biến số $x$.

Bài giải:

a) Vì mỗi giờ vòi nước chảy được $1 m^3$ nên sau $x$ giờ vòi đã chảy được: $1.x \,(m^3)$ nước.

Ban đầu trong bể chứa sẵn $3 m^3$ nước nên lượng nước $y$ có trong bể sau $x$ giờ là:

$y = 1.x + 3 = x + 3$.

b) Vẽ đồ thị hàm số $y = x + 3$

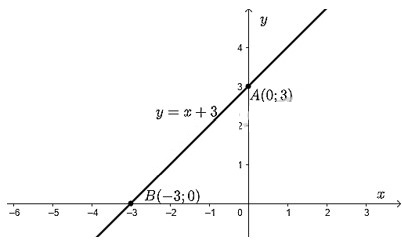
Cho $x = 0 \Rightarrow y = 3$ ta được điểm $A(0;3)$ trên trục $Oy$.

Cho $y = 0 \Rightarrow x = \dfrac{{ – 3}}{1} = – 3$ ta được điểm $B( – 3;0)$ trên $Ox$.

Đồ thị hàm số $y = x + 3$ là đường thẳng đi qua hai điểm $A;B$.

Bài trước:

👉 Giải bài 1 2 3 4 5 6 trang 22 sgk Toán 8 tập 2 Chân Trời Sáng Tạo

Bài tiếp theo:

👉 Giải Bài tập cuối chương 5 trang 28 29 sgk Toán 8 tập 2 Chân Trời Sáng Tạo

Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 10 trang 26 27 sgk Toán 8 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“