Giải bài 1 2 3 4 5 6 7 8 9 10 trang 84 sgk Toán 7 tập 2 Chân Trời Sáng Tạo

Nội Dung

Hướng dẫn giải Bài tập cuối chương 8 sgk Toán 7 tập 2 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 5 6 7 8 9 10 trang 84 sgk Toán 7 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.

GIẢI BÀI TẬP CUỐI CHƯƠNG 8

Sau đây là phần Giải bài 1 2 3 4 5 6 7 8 9 10 trang 84 sgk Toán 7 tập 2 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 trang 84 Toán 7 tập 2 CTST

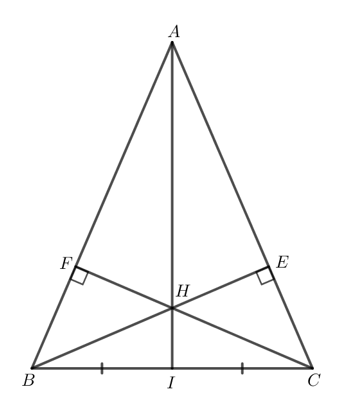
Cho tam giác ABC cân tại A ($\widehat A < {90^o}$). Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rằng $∆ BFC = ∆ CEB$.

b) Chứng minh rằng $∆ AEH = ∆ AFH$.

c) Gọi I là trung điểm BC. Chứng minh rằng ba điểm A,H,I thẳng hàng.

Bài giải:

a) Xét $∆ BFC$ và $∆ CEB$ có:

$BC là$ cạnh chung

$\widehat B = \widehat C$ ($∆ ABC$ cân tại $A$)

$\widehat {BEC} = \widehat {CFB} = {90^o}$

$⇒ ∆ BFC = ∆ CEB$ (cạnh huyền – góc nhọn)

b) Vì $∆ BFC = ∆ CEB⇒ $ BF = EC (2 cạnh tương ứng)

Mà $AB = AC$ ($∆ ABC$ cân tại $A$)

⇒ $AF = AE$ ⇒ $(AB – BF = AC – EC)$

Xét $∆ AEH$ và $∆ AFH$ có:

$AF = AE$ (chứng minh trên)

$AH$ cạnh chung

$\widehat {HFA} = \widehat {HEA} = {90^o}$

$⇒ ∆ AEH = ∆ AFH$ (cạnh huyền – cạnh góc vuông)

c) Vì $CF, BE$ là những đường cao của tam giác $ABC$ và $H$ là giao điểm của chúng

⇒ $H$ là trực tâm của tam giác $ABC$

⇒ $AH \bot BC$ (1)

Xét $∆ AIC$ và $∆ AIB$ có:

$IB = IC$ ($I$ là trung điểm $BC$)

$AI$ là cạnh chung

$AB = AC$ (tam giác $ABC$ cân tại $A$)

$⇒ ∆ AIC = ∆ AIB$ (c.c.c)

$⇒ \widehat {AIC} = \widehat {AIB}$ (2 góc tương ứng)

Mà chúng ở vị trí kề bù $⇒ \widehat {AIC} = \widehat {AIB} = {90^o}$

$⇒ AI \bot BC$ (2)

Từ (1) và (2) ⇒ $A, H, I$ thẳng hàng.

Giải bài 2 trang 84 Toán 7 tập 2 CTST

Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh rằng tam giác ABM cân.

b) Chứng minh rằng $∆ ABC = ∆ MBC$.

Bài giải:

a) Xét $∆ BHA$ và\ (∆ BHM\) có:

$\widehat {BHA} = \widehat {BHM} = {90^o}$

$BH$ cạnh chung

$AH = HM$ (do $M$ đối xứng với $A$ qua $H$)

$⇒ ∆ BHA = ∆ BHM$ (c.g.c)

$⇒ AB = BM$ (cạnh tương ứng) và $\widehat {ABH} = \widehat {MBH}$

$⇒ ∆ ABM$ cân tại $B$ (2 cạnh bên bằng nhau)

b) Xét $∆ ABC$ và $∆ MBC$ có:

$AB = BM$ (chứng minh trên)

$\widehat {ABH} = \widehat {MBH}$ (chứng minh trên)

$BC$ cạnh chung

$⇒ ∆ ABC = ∆ MBC$ (c.g.c)

Giải bài 3 trang 84 Toán 7 tập 2 CTST

Cho tam giác ABC vuông tại A ($AB < AC$), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho $HD = HC$.

a) Chứng minh rằng $AD = AC$.

b) Chứng minh rằng $\widehat {ADH} = \widehat {BAH}$.

Bài giải:

a) Xét $∆ AHD$ và $∆ AHC$ có:

$AH$ chung

$DH = HC$ (C đối xứng D qua H)

$\widehat {AHD} = \widehat {AHC} = {90^o}$

$⇒ ∆ AHD = ∆ AHC$ (c.g.c)

$⇒ AD = AC$ (cạnh tương ứng)

$⇒ ∆ ADC$ cân tại A

$⇒ \widehat C = \widehat D$ (góc tương ứng) (1)

b) Ta có $\widehat {BAH} + \widehat {HAC} = {90^o}$ và $\widehat {HCA} + \widehat {HAC} = {90^o}$

$⇒ \widehat {BAH} = \widehat {HCA}$ (2)

Từ (1) và (2) $⇒ \widehat {ADH} = \widehat {BAH}$.

Giải bài 4 trang 84 Toán 7 tập 2 CTST

Cho tam giác ABC vuông tại A ($AB < AC$). Trên cạnh BC lấy điểm N sao cho $BA = BN$. Kẻ $BE \bot AN$ (E ∈ AN).

a) Chứng minh rằng BE là tia phân giác của giác ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của BH với CE. Chứng minh rằng $NK // CA$.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh rằng tam giác GBC cân.

Bài giải:

a) Xét $∆ BAE$ và $∆ BNE$ có:

$BA = BN$ (giả thiết)

$BF$ cạnh chung

$\widehat {BEA} = \widehat {BEN}$

$⇒ ∆ BAE = ∆ BNE$ (cạnh huyền-cạnh góc vuông)

$⇒ \widehat {ABF} = \widehat {NBF}$ (góc tương ứng)

⇒ $BE$ là phân giác của góc $ABN$.

b) Vì $K$ là giao của 2 đường cao ⇒ $K$ là trực tâm tam giác $ABN$

⇒ $KN \bot AB$ (1)

Lại có $CA \bot AB$ (tam giác ABC vuông tại A) (2)

Từ (1) và (2) ⇒ $KN // CA$ (quan hệ cùng vuông góc với 1 đường)

c) Ta có $∆ BAF = ∆ BNF$ (c.g.c) do có:

$\widehat {BEA} = \widehat {BEN}$

$BF$ cạnh chung

$BN = BA$

$⇒ \widehat {BNF} = \widehat {BAF}$ (2 góc tương ứng)

Mà $\widehat {BAF} = 90^\circ $ $⇒ \widehat {BNF} = \widehat {BAF} = {90^o}$

$⇒ GN \bot BC$

Ta có $CA$ và $GN$ là 2 đường cao của tam giác $GBC$

⇒ $F$ là trực tâm của tam giác $GBC$

⇒ $BF$ vuông góc với $GC$ tại $P$

Xét $∆ BGP$ và $∆ BCP$ ta có:

$BP$ cạnh chung

$\widehat {BPC} = \widehat {BPG} = {90^o}$

$\widehat {PBC} = \widehat {PBG}$

$⇒ ∆ BGP = ∆ BCP$ (c.g.c)

$⇒ BC = BG$ (2 cạnh tương ứng)

⇒Tam giác $GBC$ cân tại $B$.

Giải bài 5 trang 84 Toán 7 tập 2 CTST

Cho tam giác nhọn ABC ($AB < AC$), vẽ đường cao AH. Đường trung trực của BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng $\widehat {BMN} = \widehat {HAC}$.

b) Kẻ $MI \bot AH$ (I ∈ AH), gọi K là giao điểm của AH và BM. Chứng minh rằng I là trung điểm của AK.

Bài giải:

a) Xét tam giác $BMC$ cân tại $M$ (Do $M$ thuộc đường trung trực của $BC$ nên $MB = MC$) có: $\widehat {MBC} = \widehat {MCB}$ (góc tương ứng)

Mà $\widehat {BMN} = {90^o} – \widehat {MBC}$ và $\widehat {HAC} = {90^o} – \widehat {BCM}$

⇒$\widehat {BMN} = \widehat {HAC}$.

b) Ta có $MN // AH$ (do cùng vuông góc với $BC$)

$⇒ \widehat {AKM} = \widehat {KMN}$ (2 góc so le trong)

Mà $\widehat {BMN} = \widehat {HAC}$ (chứng trên)

$⇒ \widehat {KAM} = \widehat {AKM}$ (do cùng =$\widehat {BMN}$)

Xét $∆ MIA$ và $∆ MIK$ có:

$IM$ cạnh chung

$\widehat {KAM} = \widehat {AKM}$

$\widehat {AIM} = \widehat {MIK} = {90^o}$

$⇒ ∆MIA = ∆MIK$ (cạnh góc vuông – góc nhọn)

⇒$AI = IK$ (cạnh tương ứng)

⇒$I$ là trung điểm $AK$.

Giải bài 6 trang 84 Toán 7 tập 2 CTST

Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho $FN = FD$.

a) Chứng minh rằng $∆ MFN = ∆ PFD$.

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của GH. Gọi K là trung điểm của GK. Chứng minh rằng ba điểm M, H, K thẳng hàng.

Bài giải:

a) Vì $N$ đối xứng với $D$ qua $F$ (theo giả thiết)

Nên $NF = DF$ (1)

Vì $F$ là trung điểm của $MP$ (theo giả thiết)

Nên $MF = PF$ (2)

Vì góc $NFM$ và góc $PFD$ ở vị trí đối đỉnh nên 2 góc bằng nhau (3)

Từ (1), (2) và (3) ⇒ $∆ MFN = ∆ PFD$ (c.g.c)

b) Xét tam giác $MPD$ có:

$F$ là trung điểm $MD$

$K$ là trung điểm $DP$ (theo giả thiết)

Mà 2 đường trung tuyến của tam giác $MPD$ là $DF$ và $MK$ cắt nhau tại $H$

⇒ $H$ là trọng tâm $∆ MPD$

⇒ $M, H, K$ thẳng hàng.

Giải bài 7 trang 84 Toán 7 tập 2 CTST

Cho tam giác ABC vuông tại A có $AB = \dfrac{1}{2}AC$, AD là tia phân giác $\widehat {BAC}$ (D ∈ BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng $DE = DB$.

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng $AH \bot KC$.

Bài giải:

a) Xét $∆ BAD$ và $∆ EAD$ có:

$AD$ là cạnh chung

$AB = AE =\dfrac{1}{2}AC$

$\widehat {BAD} = \widehat {EAD}$ (do AD là phân giác góc A)

$⇒ ∆ BAD = ∆ EAD$ (c.g.c)

⇒ $DE = DB$ (cạnh tương ứng) và $\widehat {ABD} = \widehat {AED}$ (góc tương ứng)

b) Xét $∆ KAE$ và $∆ CAB$ có:

$AE = AB$

$\widehat {ABD} = \widehat {AED}$ (chứng minh trên)

$\widehat A$ chung

$⇒ ∆ KAE = ∆ CAB$ (g.c.g)

⇒ $KE = CB$ (cạnh tương ứng)

Mà $KE = ED + DK$ và $CB = BD + DC$

⇒ $KE – ED = CB – BD$ ⇒ $DK = DC$

⇒$∆ DCK$ cân tại $D$

Xét $∆ KDB$ và $∆ CDE$ có:

$DB = DE$

$DK = DC$

$\widehat {KDB} = \widehat {CDE}$ (2 góc đối đỉnh)

$⇒ ∆ KDB = ∆ CDE$ (c.g.c)

⇒ $KB = EC ⇒ KB = AB$ (do cùng $= EC$)

⇒ $B$ là trung điểm $AK$

c) Vì $∆ KAE = ∆ CAB$ (chứng minh trên)

⇒$ AK = AC$ (cạnh tương ứng)

⇒ $∆ AKC$ vuông cân tại $A$

Mà $AD$ là phân giác góc $A$ nên $AD$ sẽ vừa là phân giác vừa là đường cao của $∆ AKC$

⇒ $AD \bot KC$

⇒ $AH \bot KC$ (do $H \in AD$).

Giải bài 8 trang 84 Toán 7 tập 2 CTST

Ở Hình 1, cho biết $AE = AF$ và $\widehat {ABC} = \widehat {ACB}$. Chứng minh AH là đường trung trực của BC.

Bài giải:

Theo giả thiết ta có tam giác $ABC$ cân tại $A$ do có 2 góc đáy bằng nhau

⇒ $A$ cách đều 2 đều $B, C$

⇒ $A$ thuộc trung trực đoạn thẳng $BC$ (1) (Tính chất điểm cách đều 2 đầu mút đoạn thẳng)

Xét $∆ AEC$ và $∆ AFB$ có:

$AE = AF$

Góc $\widehat A$ chung

$AC = AB$

$⇒ ∆ AEC = ∆ AFB$ (c.g.c)

$⇒ \widehat {ECA} = \widehat {FBA}$ (góc tương ứng)

Ta có: $\widehat {ABC} = \widehat {ABF} + \widehat {FBC}$

$\widehat {ACB} = \widehat {ACE} + \widehat {ECB}$

Mà $\widehat {ACB} = \widehat {ABC}$ (giả thiết) và $\widehat {ECA} = \widehat {FBA}$ (chứng minh trên)

$⇒ \widehat {ECB} = \widehat {FBC} ⇒∆ HBC$ cân tại $H$ do có 2 góc đáy bằng nhau.

⇒ $H$ cách đều $BC$ ⇒ $H$ thuộc trung trực $BC$ (2) (Tính chất điểm cách đều 2 đầu mút đoạn thẳng)

Từ (1) và (2) ⇒ $AH$ là trung trực của $BC$

Giải bài 9 trang 84 Toán 7 tập 2 CTST

Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho $HE = HM$.

a) Chứng minh rằng tam giác MBE cân.

b) Chứng minh rằng $\widehat {EBH} = \widehat {ACM}$.

c) Chứng minh rằng $EB \bot BC$.

Bài giải:

a) Xét $∆ BHE$ và $∆ BHM$ có:

$BH$ là cạnh chung

$EH = HM$ (do $M$ đối xứng $E$ qua $H$)

$\widehat {BHE} = \widehat {BHM} = {90^o}$

⇒$∆ BHE = ∆ BHM$ (c.g.c)

⇒ $BM = BE$ (cạnh tương ứng) và $\widehat {EBH} = \widehat {MBH}$ (góc tương ứng) (1)

⇒$∆ BEM$ cân tại $B$ (2 cạnh bên bằng nhau)

b) Xét $∆ BHM$ vuông tại $H$:

$⇒ \widehat {BMH} + \widehat {MBH} = {90^o}$

Xét $∆ AMC$ vuông tại $A$:

$⇒ \widehat {AMC} + \widehat {MCA} = {90^o}$

Mà $\widehat {HMB} = \widehat {AMC}$ (2 góc đối đỉnh)

$⇒ \widehat {MCA} = \widehat {MBH} = {90^o} – \widehat {AMC} = {90^o} – \widehat {HMB}$ (2)

Từ (1) và (2) $⇒ \widehat {EBH} = \widehat {ACM}$.

c) Vì $\widehat {BCM} = \widehat {ACM}$ (do CM là phân giác góc C)

$⇒ \widehat {EBH} = \widehat {BCM}$ (cùng bằng $\widehat {AMC}$) (3)

Xét $∆ EHB$ vuông tại $H$ có:

$\widehat {EBH} + \widehat {BEH} = {90^o}$(4)

Từ (3) và (4) $⇒ \widehat {BMC} + \widehat {BEH} = {90^o}$

$⇒ \widehat {EBC} = {90^o}$

$⇒ EB \bot BC$.

Giải bài 10 trang 84 Toán 7 tập 2 CTST

Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.

Bài giải:

Vì $b$ vuông góc với $a$ tại $J$ (theo giả thiết) và $M$ thuộc $b$

$⇒ MJ \bot IK$ (1)

Vì đường thẳng qua $I$ vuông góc với $MK$ và cắt $b$ tại $N$

$⇒ MK \bot IN$ (2)

Từ (1) và (2) ⇒$N$ là trực tâm $Δ MIK$

⇒ $NK$ là đường cao của $ΔMIK$ (Các đường cao trong tam giác đi qua trực tâm)

⇒$KN \bot MI$.

Bài trước:

👉 HĐTH&TN: Làm giàn hoa tam giác để trang trí lớp học Toán 7 tập 2 Chân Trời Sáng Tạo

Bài tiếp theo:

👉 Giải bài 1 2 3 4 trang 89 sgk Toán 7 tập 2 Chân Trời Sáng Tạo

Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 10 trang 84 sgk Toán 7 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“