Nội Dung
Hướng dẫn giải Bài §4. Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc sgk Toán 7 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 6 7 8 trang 25 26 sgk Toán 7 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§4. THỨ TỰ THỰC HIỆN CÁC PHÉP TÍNH. QUY TẮC DẤU NGOẶC
Câu hỏi khởi động trang 23 Toán 7 tập 1 CD
Làm thế nào để tính giá trị của biểu thức \(0,5 + 4,5:3 – \frac{3}{16}.\frac{4}{3}\)?
Trả lời:
Ta đổi các số thập phân trong biểu thức trên ra phân số rồi thực hiện như sau:
\(0,5 + 4,5:3 – \frac{3}{16}.\frac{4}{3}\)
\(= \frac{1}{2} + \frac{9}{2} : 3 – \frac{3}{16}.\frac{4}{3}\)
\(= \frac{1}{2} + \frac{9}{2} . \frac{1}{3} – \frac{3}{16}.\frac{4}{3}\)
\(= \frac{1}{2} + \frac{3}{2} – \frac{1}{4}\)
\(= 2 – \frac{1}{4} = \frac{7}{4}\)
I. THỨ TỰ THỰC HIỆN CÁC PHÉP TÍNH
Luyện tập vận dụng 1 trang 23 Toán 7 tập 1 CD
Tính giá trị của mỗi biểu thức sau:
a) \(0,2 + 2,5:\frac{7}{2}\);
b) \(9.{\left( {\frac{{ – 1}}{3}} \right)^2} – {\left( { – 0,1} \right)^3}:\frac{2}{{15}}\).
Trả lời:
a) Ta có:
\(0,2 + 2,5:\frac{7}{2} = \frac{2}{{10}} + \frac{25}{10}:\frac{7}{2} = \frac{1}{5} + \frac{25}{10}.\frac{2}{7} \\= \frac{1}{5} + \frac{5}{7} = \frac{7}{{35}} + \frac{{25}}{{35}} = \frac{{32}}{{35}}\)
b) Ta có:
\(\begin{array}{l}9.{\left( {\frac{{ – 1}}{3}} \right)^2} – {\left( { – 0,1} \right)^3}:\frac{2}{{15}}\\ = 9.\frac{1}{9} – {\left( {\frac{{ – 1}}{{10}}} \right)^3}:\frac{2}{{15}}\\ = 1 – \frac{{ – 1}}{{1000}}:\frac{2}{{15}}\\ = 1 – \frac{{ – 1}}{{1000}}.\frac{{15}}{2}\\ = 1 + \frac{3}{{400}}\\=\frac{400}{400}+\frac{3}{400}\\ = \frac{{403}}{{400}}\end{array}\)
Luyện tập vận dụng 2 trang 24 Toán 7 tập 1 CD
Tính giá trị của mỗi biểu thức sau:
a) \(\left( {0,25 – \frac{5}{6}} \right).1,6 + \frac{{ – 1}}{3}\);
b) \(3 – 2.\left[ {0,5 + \left( {0,25 – \frac{1}{6}} \right)} \right]\).
Trả lời:
a) Ta có:
\(\begin{array}{l}\left( {0,25 – \frac{5}{6}} \right).1,6 + \frac{{ – 1}}{3}\\ =(\frac{25}{100}-\frac{5}{6}).\frac{16}{10}+\frac{-1}{3}\\= \left( {\frac{1}{4} – \frac{5}{6}} \right).\frac{8}{5} + \frac{{ – 1}}{3}\\ = \left( {\frac{6}{{24}} – \frac{{20}}{{24}}} \right).\frac{8}{5} + \frac{{ – 1}}{3}\\ = \frac{{ – 14}}{{24}}.\frac{8}{5} + \frac{{ – 1}}{3}\\ = \frac{{ – 14}}{{15}} + \frac{{ – 1}}{3}\\ = \frac{{ – 14}}{{15}} + \frac{{ – 5}}{{15}}\\ = \frac{{ – 19}}{{15}}\end{array}\)
b) Ta có:
\(\begin{array}{l}3 – 2.\left[ {0,5 + \left( {0,25 – \frac{1}{6}} \right)} \right]\\ = 3 – 2.\left[ {\frac{1}{2} + \left( {\frac{1}{4} – \frac{1}{6}} \right)} \right]\\ = 3 – 2.\left( {\frac{1}{2} + \frac{1}{{12}}} \right)\\ =3-2.(\frac{6}{12}+\frac{1}{12})\\= 3 – 2.\frac{7}{{12}}\\ = 3 – \frac{7}{6}\\=\frac{18}{6}-\frac{7}{6}\\ = \frac{{11}}{6}\end{array}\)
II. QUY TẮC DẤU NGOẶC
Luyện tập vận dụng 3 trang 25 Toán 7 tập 1 CD
Tính một cách hợp lí:
a) \(1,8 – \left( {\frac{3}{7} – 0,2} \right)\);
b) \(12,5 – \frac{{16}}{{13}} + \frac{3}{{13}}\).
Trả lời:
a) Ta có:
\(\begin{array}{l}1,8 – \left( {\frac{3}{7} – 0,2} \right)\\ = 1,8 – \frac{3}{7} + 0,2\\ = \left( {1,8 + 0,2} \right) – \frac{3}{7}\\ = 2 – \frac{3}{7} = \frac{{11}}{7}\end{array}\)
b) Ta có:
\(\begin{array}{l}12,5 – \frac{{16}}{{13}} + \frac{3}{{13}}\\ = 12,5 – \frac{{16}}{{13}} + \frac{3}{{13}}\\ = 12,5 + \left( { – \frac{{16}}{{13}} + \frac{3}{{13}}} \right)\\ = 12,5 + \left( { – 1} \right) = 11,5\end{array}\)
Luyện tập vận dụng 4 trang 25 Toán 7 tập 1 CD
Tính một cách hợp lí:
a) \(\left( { – \frac{5}{6}} \right) – \left( { – 1,8} \right) + \left( { – \frac{1}{6}} \right) – 0,8\);
b) \(\left( { – \frac{9}{7}} \right) + \left( { – 1,23} \right) – \left( { – \frac{2}{7}} \right) – 0,77\).
Trả lời:
a) Ta có:
\(\begin{array}{l}\left( { – \frac{5}{6}} \right) – \left( { – 1,8} \right) + \left( { – \frac{1}{6}} \right) – 0,8\\ = \left( { – \frac{5}{6}} \right) + 1,8 + \left( { – \frac{1}{6}} \right) – 0,8\\ = \left[ {\left( { – \frac{5}{6}} \right) + \left( { – \frac{1}{6}} \right)} \right] + \left[ {1,8 – 0,8} \right]\\ = – 1 + 1 = 0\end{array}\)
b) Ta có:
\(\begin{array}{l}\left( { – \frac{9}{7}} \right) + \left( { – 1,23} \right) – \left( { – \frac{2}{7}} \right) – 0,77\\ = \left[ {\left( { – \frac{9}{7}} \right) – \left( { – \frac{2}{7}} \right)} \right] + \left[ {\left( { – 1,23} \right) – 0,77} \right]\\ = – 1 + \left( { – 2} \right) = – 3\end{array}\)
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 7 8 trang 25 26 sgk Toán 7 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 25 Toán 7 tập 1 CD
Tính:
a) \(\frac{1}{9} – 0,3.\frac{5}{9} + \frac{1}{3};\)
b) \({\left( {\frac{{ – 2}}{3}} \right)^2} + \frac{1}{6} – {\left( { – 0,5} \right)^3}.\)
Bài giải:
a) Ta có:
\(\begin{array}{l}\frac{1}{9} – 0,3.\frac{5}{9} + \frac{1}{3}\\ = \frac{1}{9} – \frac{3}{{10}}.\frac{5}{9} + \frac{1}{3}\\ = \frac{1}{9} – \frac{3}{{2.5}}.\frac{5}{{3.3}} + \frac{1}{3}\\ = \frac{1}{9} – \frac{1}{6} + \frac{1}{3}\\ = \frac{2}{{18}} – \frac{3}{{18}} + \frac{6}{{18}}\\ = \frac{5}{{18}}\end{array}\)
b) Ta có:
\(\begin{array}{l}{\left( {\frac{{ – 2}}{3}} \right)^2} + \frac{1}{6} – {\left( { – 0,5} \right)^3}\\ = \frac{4}{9} + \frac{1}{6} – \left( {\frac{{ – 1}}{8}} \right)\\ = \frac{4}{9} + \frac{1}{6} + \frac{1}{8}\\ = \frac{{32}}{{72}} + \frac{{12}}{{72}} + \frac{9}{{72}}\\ = \frac{{53}}{{72}}\end{array}\)
Giải bài 2 trang 25 Toán 7 tập 1 CD
Tính:
a) \(\left( {\frac{4}{5} – 1} \right):\frac{3}{5} – \frac{2}{3}.0,5\);
b) \(1 – {\left( {\frac{5}{9} – \frac{2}{3}} \right)^2}:\frac{4}{{27}}\);
c)\(\left[ {\left( {\frac{3}{8} – \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\);
d) \(0,8:\left\{ {0,2 – 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} – \frac{5}{{14}}} \right)} \right]} \right\}\).
Bài giải:
a) Ta có:
\(\begin{array}{l}\left( {\frac{4}{5} – 1} \right):\frac{3}{5} – \frac{2}{3}.0,5\\ = \frac{{ – 1}}{5}.\frac{5}{3} – \frac{2}{3}.\frac{1}{2}\\ = \frac{{ – 1}}{3} – \frac{1}{3}\\ = \frac{{ – 2}}{3}\end{array}\)
b) Ta có:
\(\begin{array}{l}1 – {\left( {\frac{5}{9} – \frac{2}{3}} \right)^2}:\frac{4}{{27}}\\ = 1 – {\left( {\frac{5}{9} – \frac{6}{9}} \right)^2}:\frac{4}{{27}}\\ = 1 – {\left( {\frac{{ – 1}}{9}} \right)^2}.\frac{{27}}{4}\\ = 1 – \frac{1}{{81}}.\frac{{27}}{4}\\ = 1 – \frac{1}{{12}}\\ = \frac{{11}}{{12}}\end{array}\)
c) Ta có:
\(\begin{array}{l}\left[ {\left( {\frac{3}{8} – \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} – \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} – \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ – 1}}{{24}}.6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ – 1}}{4} + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ – 3}}{{12}} + \frac{4}{{12}}} \right].4\\ = \frac{1}{{12}}.4 = \frac{1}{3}\end{array}\)
d) Ta có:
\(\begin{array}{l}0,8:\left\{ {0,2 – 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} – \frac{5}{{14}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} – 7.\left[ {\frac{1}{6} + \left( {\frac{{10}}{{42}} – \frac{{15}}{{42}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} – 7.\left[ {\frac{7}{{42}} + \frac{{ – 5}}{{42}}} \right]} \right\}\\ = \frac{4}{5}:\left( {\frac{1}{5} – 7.\frac{2}{{42}}} \right)\\ = \frac{4}{5}:\left( {\frac{1}{5} – \frac{1}{3}} \right)\\ =\frac{4}{5}:\left( {\frac{3}{15} – \frac{5}{{15}}} \right)\\ = \frac{4}{5}:\frac{{ – 2}}{{15}}\\ = \frac{4}{5}.\frac{{ – 15}}{2}\\ = – 6\end{array}\)
Giải bài 3 trang 26 Toán 7 tập 1 CD
Chọn dấu ” “=”, ” \( \ne \) ” thích hợp cho dấu ⍰:
a) \(\frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5\) ⍰ \(\frac{{28}}{9} \cdot (0,7 + 0,5)\);
b) \(\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9\) ⍰ \(\frac{{36}}{{13}}:(4 + 9)\).
Bài giải:
a) Ta có:
\(\frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5 = \frac{{28}}{9}.\left( {0,7 + 0,5} \right)\)
b) Ta có:
\(\begin{array}{l}\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9\\ = \frac{{36}}{{13}}.\frac{1}{4} + \frac{{36}}{{13}}.\frac{1}{9}\\ = \frac{{36}}{{13}}.\left( {\frac{1}{4} + \frac{1}{9}} \right)\\ = \frac{{36}}{{13}}.\frac{{13}}{{36}} = 1\end{array}\)
\(\begin{array}{l}\frac{{36}}{{13}}:(4 + 9)\\ = \frac{{36}}{{13}}:13\\ = \frac{{36}}{{13}}.\frac{1}{{13}}\\ = \frac{{36}}{{169}}\end{array}\)
Suy ra \(\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9\) \( \ne \) \(\frac{{36}}{{13}}:(4 + 9)\).
Giải bài 4 trang 26 Toán 7 tập 1 CD
Tính một cách hợp lí:
a) \(\frac{4}{{15}} – \left( {2,9 – \frac{{11}}{{15}}} \right)\);
b) \(( – 36,75) + \left( {\frac{{37}}{{10}} – 63,25} \right) – ( – 6,3)\);
c) \(6,5 + \left( { – \frac{{10}}{{17}}} \right) – \left( { – \frac{7}{2}} \right) – \frac{7}{{17}}\);
d) \(( – 39,1) \cdot \frac{{13}}{{25}} – 60,9 \cdot \frac{{13}}{{25}}\).
Bài giải:
a) Ta có:
\(\begin{array}{l}\frac{4}{{15}} – \left( {2,9 – \frac{{11}}{{15}}} \right)\\ = \frac{4}{{15}} – 2,9 + \frac{{11}}{{15}}\\ = \left( {\frac{4}{{15}} + \frac{{11}}{{15}}} \right) – 2,9\\=\frac{15}{15}-2,9 \\= 1 – 2,9 = – 1,9\end{array}\)
b) Ta có:
\(\begin{array}{l}( – 36,75) + \left( {\frac{{37}}{{10}} – 63,25} \right) – ( – 6,3)\\ = ( – 36,75) + 3,7 – 63,25 + 6,3\\ = \left( { – 36,75 – 63,25} \right) + \left( {3,7 + 6,3} \right)\\ = – 100 + 10 = – 90\end{array}\)
c) Ta có:
\(\begin{array}{l}6,5 + \left( { – \frac{{10}}{{17}}} \right) – \left( { – \frac{7}{2}} \right) – \frac{7}{{17}}\\ = \frac{{65}}{{10}} – \frac{{10}}{{17}} + \frac{7}{2} – \frac{7}{{17}}\\ = \left( {\frac{{65}}{{10}} + \frac{7}{2}} \right) – \left( {\frac{{10}}{{17}} + \frac{7}{{17}}} \right)\\ = \left( {\frac{{65}}{{10}} + \frac{{35}}{{10}}} \right) – \frac{17}{17}\\ = \frac{100}{10}-1\\=10 – 1 = 9\end{array}\)
d) Ta có:
\(\begin{array}{l}( – 39,1) \cdot \frac{{13}}{{25}} – 60,9 \cdot \frac{{13}}{{25}}\\ = \frac{{13}}{{25}}.\left( { – 39,1 – 60,9} \right)\\ = \frac{{13}}{{25}}.\left( { – 100} \right)\\ = – 52\end{array}\).
Giải bài 5 trang 26 Toán 7 tập 1 CD
Một mảnh vườn có dạng hình chữ nhật với độ dài hai cạnh là 5,5 m và 3,75 m. Dọc theo các cạnh của mảnh vườn, người ta trồng các khóm hoa, cứ \(\frac{1}{4}\)m trồng một khóm hoa. Tính số khóm hoa cần trồng.
Bài giải:
Chu vi mảnh vườn hình chữ nhật là:
\(\left( {5,5 + 3,75} \right).2 = 18,5\) (m)
Số khóm hoa cần trồng là:
\(18,5:\frac{1}{4} = 74\) (khóm)
Giải bài 6 trang 26 Toán 7 tập 1 CD
Cho miếng bìa có kích thước như hình vẽ bên (các số đo trên hình tính theo đơn vị đề-xi-mét).
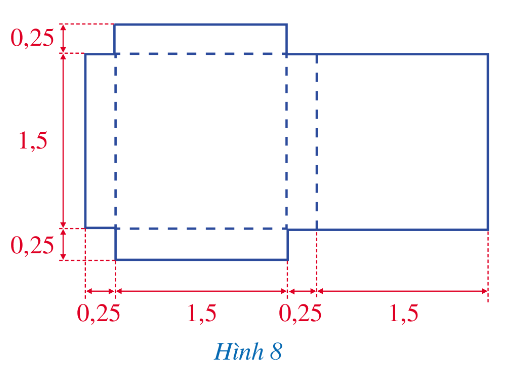
a) Tính diện tích của miếng bìa.
b) Từ miếng bìa đó, người ta gấp thành một hình hộp chữ nhật. Tính thể tích của hình hộp chữ nhật đó.
Bài giải:
a) Diện tích miếng bìa là:
\(\left( {0,25 + 1,5 + 0,25 + 1,5} \right).1,5 + 2.0,25.1,5 = 3,5.1,5 + 0,5.1,5 = 1,5.4 = 6\)(dm2)
b) Thể tích hình hộp chữ nhật là:
\(1,5.0,25.1,5 = 0,5625\)(dm3)
Hoặc:
a) Đặt tên các điểm trên miếng lần lượt là A, B, C, D, E, F, G, H, I, K, L, M, N như hình vẽ:
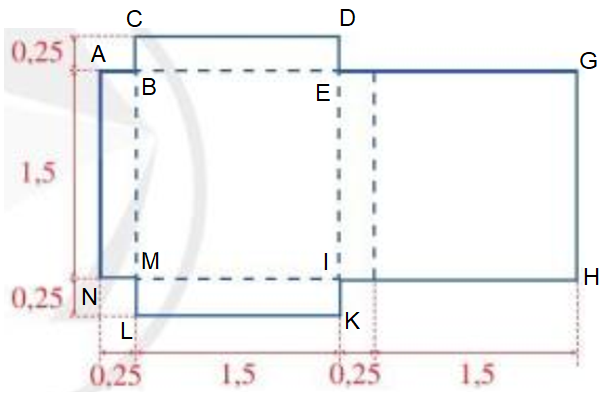
Ta có thể chia miếng bìa thành các hình nhỏ, sau đó tính tổng diện tích của các hình nhỏ đó.
Có nhiều các chia thành các hình nhỏ. Chẳng hạn:
♦ Cách 1: Ta chia miếng bìa đã cho thành 3 hình chữ nhật: ABMN, CDKL, EGHI.
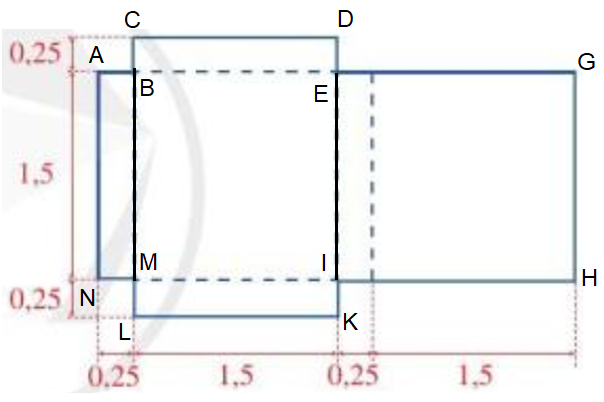
Diện tích hình chữ nhật ABMN là:
1,5 . 0,25 = 0,375 (dm2)
Chiều dài hình chữ nhật CDKL là:
0,25 + 1,5 + 0,25 = 2 (dm)
Diện tích hình chữ nhật CDKL là:
2 . 1,5 = 3 (dm2)
Chiều dài hình chữ nhật EGHI là:
1,5 + 0,25 = 1,75 (dm)
Diện tích hình chữ nhật EGHI là:
1,75 . 1,5 = 2,625 (dm2)
Diện tích miếng bìa đã cho là:
0,375 + 3 + 2,625 = 6 (dm2)
Vậy diện tích miếng bìa đã cho là 6 dm2.
♦ Cách 2: Ta chia miếng bìa đã cho thành 3 hình chữ nhật: BCDE, AGHN, MIKL.
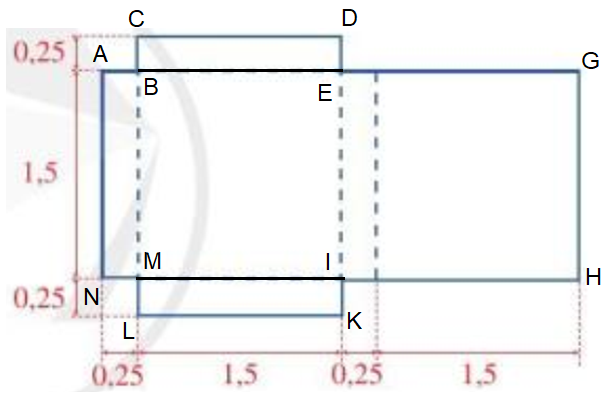
Diện tích hình chữ nhật BCDE là:
1,5 . 0,25 = 0,375 (dm2)
Chiều dài hình chữ nhật AGHN là:
0,25 + 1,5 + 0,25 + 1,5 = 3,5 (dm)
Diện tích hình chữ nhật AGHN là:
3,5 . 1,5 = 5,25 (dm2)
Diện tích hình chữ nhật MIKL là:
1,5 . 0,25 = 0,375 (dm2)
Diện tích miếng bìa đã cho là:
0,375 + 5,25 + 0,375 = 6 (dm2)
b) Từ miếng bìa đó, ta gấp được hình hộp chữ nhật có ba kích thước là: 1,5 dm; 1,5 dm và 0,25 dm.
Khi đó thể tích của hình hộp chữ nhật đó là:
1,5 . 1,5 . 0,25 = 0,5625 (dm3).
Vậy thể tích của hình hộp chữ nhật được gấp thành là 0,5625 dm3.
Giải bài 7 trang 26 Toán 7 tập 1 CD
Giá niêm yết của một chiếc ti vi ở cửa hàng là 20 000 000 đồng. Cửa hàng giảm lần thứ nhất 5% giá niêm yết của chiếc ti vi đó. Để nhanh chóng bán hết số lượng ti vi, cửa hàng giảm thêm 2% của giá ti vi sau lần giảm giá thứ nhất. Hỏi khách hàng phải trả bao nhiêu tiền cho chiếc ti vi đó sau 2 lần giảm giá?
Bài giải:
Do cửa hàng giảm giá lần thứ nhất \(5\% \) giá niêm yết nên giá ti vi sau lần giảm thứ nhất bằng \(100\%-5\% = 95\%\) giá niêm yết và bằng:
\(20000000.95\%=19000000\) (đồng)
Do cửa hàng giảm giá lần thứ hai \(2\% \) giá của lần giảm thứ nhất nên giá ti vi sau lần giảm thứ hai bằng \(100\%-2\% = 98\%\) giá của lần giảm thứ hai và bằng:
\(19000000.98\%=18620000\) (đồng)
Vậy khách hàng phải trả $18 620 000$ đồng sau $2$ lần giảm giá.
Giải bài 8 trang 26 Toán 7 tập 1 CD
Chủ cửa hàng bỏ ra 35 000 000 đồng mua một loại sản phẩm để bán. Chủ cửa hàng đã bán \(\frac{6}{7}\) số sản phẩm mua về đó với giá bán cao hơn \(10\% \) so với giá mua vào và bán \(\dfrac{1}{7}\) số sản phẩm còn lại với giá bán mỗi sản phẩm thấp hơn \(25\% \) so với giá mua vào.
a) Tính số tiền chủ cửa hàng thu về khi bán hết số sản phẩm đó.
b) Chủ cửa hàng đã lãi hay lỗ bao nhiêu phần trăm?
Bài giải:
a) Số sản phẩm bán với giá thấp hơn 25% có giá gốc là:
\(\frac{1}{7}\).35 000 000 = 5 000 000 (đồng)
Số sản phẩm bán với giá cao hơn 10% có giá gốc là:
35 000 000 – 5 000 000 = 30 000 000 (đồng)
Cửa hàng bán số sản phẩm bán với giá thấp hơn 25% được số tiền là:
5 000 000 .\(\)\(\frac{{75}}{{100}}\) = 3 750 000 (đồng)
Cửa hàng bán số sản phẩm bán với giá cao hơn 10% được số tiền là:
30 000 000 . \(\frac{{110}}{{100}}\)= 33 000 000 (đồng)
Số tiền cửa hàng thu về khi bán hết số sản phẩm là:
3 750 000 + 33 000 000 =36 750 000 (đồng)
b) Chủ cửa hàng lãi số tiền là:
36 750 000 – 35 000 000 = 1 750 000 (đồng)
Chủ cửa hàng lãi:
\(\frac{{1\,\,750\,\,000}}{{35\,000\,000}}.100\% = 5\% \)
Bài trước:
👉 Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 20 21 sgk Toán 7 tập 1 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 trang 29 sgk Toán 7 tập 1 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 trang 25 26 sgk Toán 7 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
