Nội Dung
Hướng dẫn giải Bài 2. Tia phân giác sgk Toán 7 tập 1 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 5 6 7 trang 75 sgk Toán 7 tập 1 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
BÀI 2. TIA PHÂN GIÁC
Hoạt động khởi động trang 73 Toán 7 tập 1 CTST
Khi làm con diều như hình bên thì tia DB nằm ở vị trí nào của \(\widehat {ADC}\)?
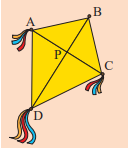
Trả lời:
Sau bài học này chúng ta biết được tia DB là tia phân giác của góc \(\widehat {ADC}\).
1. TIA PHÂN GIÁC CỦA MỘT GÓC
Hoạt động khám phá 1 trang 73 Toán 7 tập 1 CTST
Vẽ \(\widehat {xOy}\) lên một tờ giấy như trong hình 1a. Gấp giấy sao cho cạnh Oy trùng với cạnh Ox. Nếp gấp cho ta vị trí của tia Oz. Theo em, tia Oz đã chia\(\widehat {xOy}\) thành hai góc như thế nào?
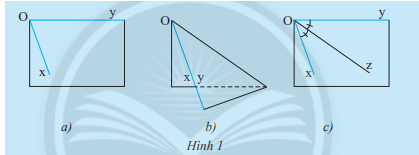
Trả lời:
Theo em, tia Oz đã chia \(\widehat {xOy}\) thành hai góc bằng nhau.
Thực hành 1 trang 73 Toán 7 tập 1 CTST
Tìm tia phân giác của các góc: \(\widehat {AOC}\) và \(\widehat {COB}\) trong Hình 3.
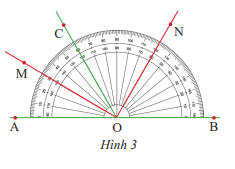
Trả lời:
Từ hình vẽ ta thấy:
Tia OM là tia phân giác của góc \(\widehat {AOC}\) (vì điểm M nằm trong góc \(\widehat {AOC}\) và \(\widehat {AOM} = \widehat {MOC} = 30^\circ \))
Tia ON là tia phân giác của góc \(\widehat {BOC}\) (vì điểm N nằm trong góc \(\widehat {BOC}\) và \(\widehat {BON} = \widehat {NOC} = 60^\circ \))
Vận dụng 1 trang 74 Toán 7 tập 1 CTST
Em hãy cho biết khi cân thăng bằng thì kim ở vị trí nào của \(\widehat {AOB}\) (Hình 4).
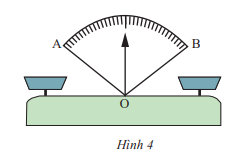
Trả lời:
Khi cân thăng bằng thì kim là tia phân giác của \(\widehat {AOB}\).
2. CÁCH VẼ TIA PHÂN GIÁC
Hoạt động khám phá 2 trang 74 Toán 7 tập 1 CTST
Trong Hình 5, nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì số đo của \(\widehat {xOy}\) bằng bao nhiêu?
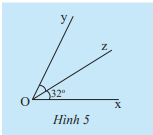
Trả lời:
Vì tia Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy}\) và \(\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\)
Như vậy \(\widehat {yOz} = 32^\circ \) nên \(\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\) = \(32^\circ + 32^\circ = 64^\circ \)
Vậy nếu Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOy} = 64^\circ \).
Chú ý: Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\).
Thực hành 2 trang 74 Toán 7 tập 1 CTST
Vẽ một góc có số đo bằng 60 \(^\circ \) rồi vẽ tia phân giác của góc đó.
Trả lời:
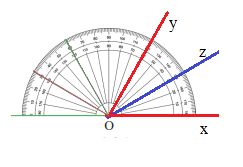
Ta sử dụng eke vẽ được \(\widehat {xOy} = 60^\circ \) và $oz$ tia phân giác của \(\widehat {xOy}\).
Vận dụng 2 trang 74 Toán 7 tập 1 CTST
Hãy vẽ một góc bẹt \(\widehat {AOB}\) rồi vẽ tia phân giác của góc đó.
Trả lời:
Ta vẽ hai đường thẳng vuông góc với nhau thỏa mãn yêu cầu của đề bài.
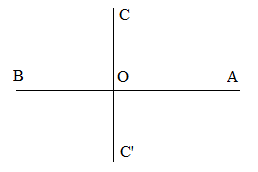
Chú ý: Góc bẹt có 2 tia phân giác là 2 tia đối nhau.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 7 trang 75 sgk Toán 7 tập 1 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 75 Toán 7 tập 1 CTST
a) Trong Hình 8, tìm tia phân giác của góc \(\widehat {ABC},\widehat {ADC}\)
b) Cho biết \(\widehat {ABC} = 100^\circ ;\widehat {ADC} = 60^\circ \). Tính số đo của các góc \(\widehat {ABO},\widehat {ADO}\)
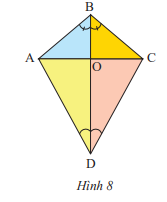
Bài giải:
a) Từ hình vẽ ta thấy:
Tia BO là tia phân giác của \(\widehat {ABC}\) vì tia BO nằm giữa 2 tia BA và BC, tạo với 2 cạnh BA và BC 2 góc bằng nhau.
Tia DO là tia phân giác của \(\widehat {ADC}\) vì tia DO nằm giữa 2 tia DA và DC, tạo với 2 cạnh DA và DC 2 góc bằng nhau.
b) Vì BO là tia phân giác của \(\widehat {ABC}\) nên
\(\widehat {ABO} = \widehat {CBO} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.100^\circ = 50^\circ \)
Vì DO là tia phân giác của \(\widehat {ADC}\) nên
\(\widehat {ADO} = \widehat {CDO} = \frac{1}{2}.\widehat {ADC} = \frac{1}{2}.60^\circ = 30^\circ \)
Vậy \(\widehat {ABO} = 50^\circ ;\widehat {ADO} = 30^\circ \)
Giải bài 2 trang 75 Toán 7 tập 1 CTST
a) Vẽ \(\widehat {xOy}\) có số đo là 110 \(^\circ \).
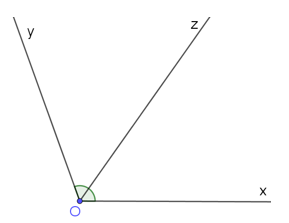
b) Vẽ tia phân giác của \(\widehat {xOy}\) trong câu a
Bài giải:
a) Ta sử dụng eke vẽ được \(\widehat {xOy} = 110^\circ \).
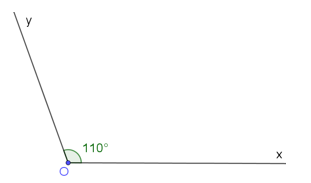
b) Ta sử dụng eke vẽ được $oz$ tia phân giác của \(\widehat {xOy}\).
Giải bài 3 trang 75 Toán 7 tập 1 CTST
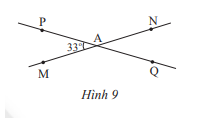
Cho đường thẳng MN, PQ cắt nhau tại A và tạọ thành \(\widehat {PAM} = 33^\circ \) (Hình 9)
a) Tính số đo các góc còn lại.
b) Vẽ tia At là tia phân giác của \(\widehat {PAN}\). Hãy tính số đo của \(\widehat {tAQ}\). Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của \(\widehat {MAQ}\)
Bài giải:
a) Ta có: \(\widehat {PAM} = \widehat {QAN}\) (2 góc đối đỉnh), mà \(\widehat {PAM} = 33^\circ \) nên \(\widehat {QAN} = 33^\circ \)
Vì \(\widehat {PAN} + \widehat {PAM} = 180^\circ \) (2 góc kề bù) nên
\(\widehat {PAN} + 33^\circ = 180^\circ \Rightarrow \widehat {PAN} = 180^\circ – 33^\circ = 147^\circ \)
Vì \(\widehat {PAN} = \widehat {QAM}\) (2 góc đối đỉnh), mà \(\widehat {PAN} = 147^\circ \) nên \(\widehat {QAM} = 147^\circ \).
b) Ta vẽ hình như sau:
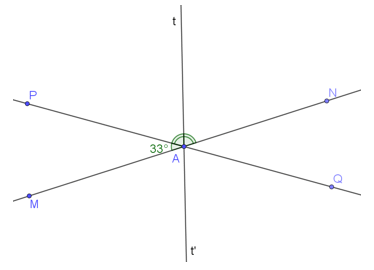
Vì At là tia phân giác của \(\widehat {PAN}\) nên
\(\widehat {PAt} = \widehat {tAN} = \frac{1}{2}.\widehat {PAN} = \frac{1}{2}.147^\circ = 73,5^\circ \)
Vì \(\widehat {tAQ} + \widehat {PAt} = 180^\circ \) (2 góc kề bù) nên
\(\widehat {tAQ} + 73,5^\circ = 180^\circ \Rightarrow \widehat {tAQ} = 180^\circ – 73,5^\circ = 106,5^\circ \)
Vẽ At’ là tia đối của tia At, ta được \(\widehat {QAt’} = \widehat {PAt}\) (2 góc đối đỉnh)
Ta có: \(\widehat {QAt’} = \widehat {MAt’} = \frac{1}{2}.\widehat {MAQ}\) nên At’ là tia phân giác của \(\widehat {MAQ}\).
Chú ý: 2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau.
Giải bài 4 trang 75 Toán 7 tập 1 CTST
Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho \(\widehat {xOz} = 135^\circ \). Vẽ tia Ot sao cho \(\widehat {yOt} = 90^\circ \) và \(\widehat {zOt} = 135^\circ \). Gọi Ov là tia phân giác của \(\widehat {xOt}\). Các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) có phải là hai góc đối đỉnh không? Vì sao?
Bài giải:
Ta vẽ hình như sau:
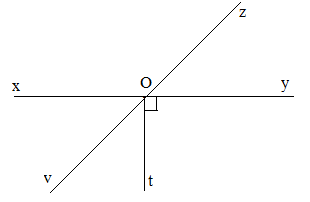
Vì \(\widehat {yOt} = 90^\circ \Rightarrow Oy \bot Ot \Rightarrow Ox \bot Ot\) nên \(\widehat {xOt} = 90^\circ \)
Vì Ov là tia phân giác của \(\widehat {xOt}\) nên
\(\widehat {xOv} = \widehat {vOt} = \frac{1}{2}.\widehat {xOt} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì \(\widehat {vOx} + \widehat {xOz} = 45^\circ + 135^\circ = 180^\circ \) nên Ov và Oz là hai tia đối nhau.
Như vậy, các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) là hai góc đối đỉnh vì Ox là tia đối của tia Oy, tia Ov là tia đối của tia Oz.
Giải bài 5 trang 75 Toán 7 tập 1 CTST
Vẽ hai góc kề bù \(\widehat {xOy},\widehat {yOx’}\), biết \(\widehat {xOy} = 142^\circ \). Gọi Oz là tia phân giác của \(\widehat {xOy}\). Tính \(\widehat {x’Oz}\)
Bài giải:
Ta vẽ hình như sau:
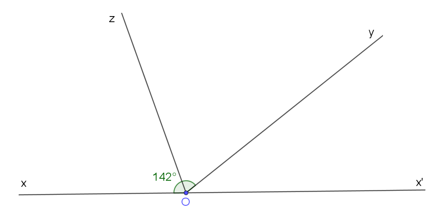
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên
\(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.142^\circ = 71^\circ \)
Mà \(\widehat {x’Oz}\) và \(\widehat {xOz}\) là 2 góc kề bù nên
\(\widehat {xOz} + \widehat {x’Oz} = 180^\circ \Rightarrow 71^\circ + \widehat {x’Oz} = 180^\circ \)
\(\Rightarrow \widehat {x’Oz} = 180^\circ – 71^\circ = 109^\circ \)
Vậy \(\widehat {x’Oz} = 109^\circ \).
Giải bài 6 trang 75 Toán 7 tập 1 CTST
Vẽ hai góc kề bù \(\widehat {xOy},\widehat {yOx’}\), biết \(\widehat {xOy} = 120^\circ \). Gọi Oz là tia phân giác của \(\widehat {xOy}\), Oz’ là tia phân giác của \(\widehat {yOx’}\). Tính \(\widehat {zOy},\widehat {yOz’},\widehat {zOz’}\)
Bài giải:
Ta vẽ hình như sau:
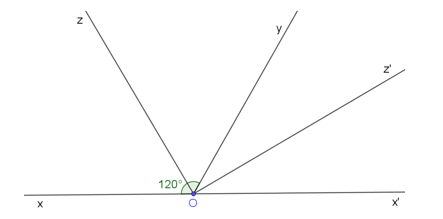
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên
\(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx’}\) nên
\(\widehat {x’Oz’} = \widehat {yOz’} = \frac{1}{2}.\widehat {yOx’} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz’}\) nên
\(\widehat {zOz’}=\widehat {zOy} + \widehat {yOz’} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz’} = 30^\circ ,\widehat {zOz’} = 90^\circ \)
Chú ý: 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Giải bài 7 trang 75 Toán 7 tập 1 CTST
Vẽ góc bẹt \(\widehat {xOy}\). Vẽ tia phân giác Oz của góc đó. Vẽ tia phân giác Ot của \(\widehat {xOz}\). Vẽ tia phân giác Ov của \(\widehat {zOy}\) . Tính \(\widehat {tOv}\)
Bài giải:
Ta vẽ hình như sau:
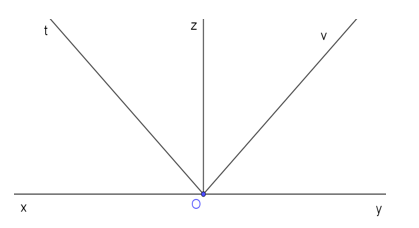
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên
\(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\) = \(\frac{1}{2}.180^\circ = 90^\circ \)
Vì Ot là tia phân giác của \(\widehat {xOz}\) nên
\(\widehat {xOt} = \widehat {tOz} = \frac{1}{2}\widehat {xOz} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì Ov là tia phân giác của \(\widehat {zOy}\) nên
\(\widehat {yOv} = \widehat {vOz} = \frac{1}{2}\widehat {zOy} = \frac{1}{2}.90^\circ = 45^\circ \)
Mà tia Oz nằm trong \(\widehat {tOv}\) nên
\(\widehat {tOv}= \widehat {tOz} + \widehat {zOv} = 45^\circ + 45^\circ = 90^\circ \)
Vậy \(\widehat {tOv} = 90^\circ \).
Bài trước:
👉 Giải bài 1 2 3 4 5 trang 72 sgk Toán 7 tập 1 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 7 trang 80 81 sgk Toán 7 tập 1 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 trang 75 sgk Toán 7 tập 1 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
