Giải bài 1 2 3 4 5 6 trang 22 sgk Toán 8 tập 2 Chân Trời Sáng Tạo

Nội Dung

Hướng dẫn giải Bài 3. Hàm số bậc nhất $y = ax + b (a≠0)$ sgk Toán 8 tập 2 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 5 6 trang 22 sgk Toán 8 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.

BÀI 3. HÀM SỐ BẬC NHẤT $y = ax + b (a≠0)$

Hoạt động khởi động trang 16 Toán 8 tập 2 CTST

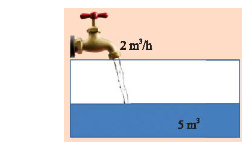
Có một cái bể đã chứa sẵn $5 {m^3}$ nước. Người ta bắt đầu mở một vòi nước cho chảy vào bể, mỗi giờ chảy được $2 {m^3}$. Hãy tính:

a) Lượng nước chảy vào bể sau $1$ giờ.

b) Lượng nước chảy vào bể sau $x$ giờ.

c) Lượng nước $y$ có trong bể sau $x$ giờ.

Trả lời:

a) Lượng nước chảy vào bể sau $1$ giờ là:

$1.2 = 2(m^3)$

b) Lượng nước chảy vào bể sau $x$ giờ là:

$2.x = 2x(m^3)$

c) Lượng nước $y$ có trong bể sau $x$ giờ là:

$y = 2x + 5(m^3)$.

1. HÀM SỐ BẠC NHẤT

Hoạt động khám phá 1 trang 16 Toán 8 tập 2 CTST

Trong thực tế chúng ta thường gặp các mô hình dẫn đến những hàm số có dạng như: $y = 2x + 5;y = – x + 4;y = 5x…$.

Những hàm số này được gọi là hàm số bậc nhất. Vậy hàm số bậc nhất có dạng như thế nào?

Trả lời:

Ta thấy tất cả các hàm số đã cho đều có dạng $y = ax + b$

$y = 2x + 5$ với $a = 2;b = 5$;

$y = – x + 4$ với $a = – 1;b = 4$;

$y = 5x$ với $a = 5;b = 0$.

Do đó, hàm số bậc nhất là hàm số được cho bởi công thức $y = ax + b$ với $a, \,b$ là các số cho trước và $a \ne 0$.

Thực hành 1 trang 16 Toán 8 tập 2 CTST

Tìm các hàm số bậc nhất trong các hàm số sau đây và chỉ ra các hệ số $a,b$ của các hàm số đó:

$y = 4x – 7$; $y = {x^2}$; $y = – 6x – 4$; $y = 4x$; $y = \dfrac{3}{x}$; $s = 5v + 8$; $m = 30n – 25$.

Trả lời:

– Hàm số$y = 4x – 7$ là hàm số bậc nhất vì hàm số có dạng $y = ax + b$với $a, \,b$ là các số cho trước và $a \ne 0$. Hệ số $a = 4; b = – 7$.

– Hàm số $y = {x^2}$ không là hàm số bậc nhất vì hàm số không có dạng $y = ax + b$ với $a, \,b$ là các số cho trước và $a \ne 0$.

– Hàm số $y = – 6x – 4$ là hàm số bậc nhất vì hàm số có dạng $y = ax + b$ với $a, \,b$ là các số cho trước và $a \ne 0$. Hệ số $a = – 6; b = – 4$.

– Hàm số $y = 4x$ là hàm số bậc nhất vì hàm số có dạng $y = ax + b$ với $a, \,b$ là các số cho trước và $a \ne 0$. Hệ số $a = 4; b = 0$.

– Hàm số $y = \dfrac{3}{x}$ không là hàm số bậc nhất vì hàm số không có dạng $y = ax + b$ với $a,b$ là các số cho trước và $a \ne 0$.

– Hàm số $s = 5v + 8$ là hàm số bậc nhất vì hàm số có dạng $s = av + b$với $a,b$ là các số cho trước và $a \ne 0$. Hệ số $a = 5; b = 8$.

– Hàm số $m = 30n – 25$ là hàm số bậc nhất vì hàm số có dạng $m = an + b$ với $a, b$ là các số cho trước và $a \ne 0$. Hệ số $a = 30; b = – 25$.

Vận dụng 1 trang 16 Toán 8 tập 2 CTST

Một hình chữ nhật có các kích thước là $2 m$ và $3 m$. Gọi $y$ là chu vi của hình chữ nhật này sau khi tăng chiều dài và chiều rộng thêm $x (m)$. Hãy chứng tỏ $y$là một hàm số bậc nhất theo biến số $x$. Tìm các hệ số $a; \,b$ của hàm số này.

Trả lời:

Sau khi tăng chiều dài thêm $x(m)$ thì chiều dài mới của hình chữ nhật là $3 + x(m)$.

Sau khi tăng chiều rộng thêm $x(m)$ thì chiều rộng mới của hình chữ nhật là $2 + x(m)$.

Chu vi mới của hình chữ nhật là:

$y = (3 + x + 2 + x).2$

$⇔ y = (5 + 2x).2$

$⇔ y = 4x + 10$

Vì hàm số $y = 4x + 10$ có dạng $y = ax + b$ với $a,b$ là các số cho trước và $a \ne 0$.

Nên hàm số $y = 4x + 10$ là hàm số bậc nhất.

Do đó $y$ là một hàm số bậc nhất theo biến số $x$, hệ số $a = 4;b = 10$.

2. BẢNG GIÁ TRỊ CỦA HÀM SỐ BẬC NHẤT

Hoạt động khám phá 2 trang 17 Toán 8 tập 2 CTST

Lượng nước $y$ (tính theo ${m^3}$) có trong một bể nước sau $x$ giờ mở vòi cấp nước được cho bởi hàm số $y = 2x + 3$. Tính lượng nước có trong bể sau $0$ giờ; $1$ giờ; $2$ giờ; $3$ giờ; $10$ giờ và hoàn thành bảng giá trị sau:

$x$	0	1	2	3	10
$y = f(x) = 2x + 3$	?	?	?	?	?

Trả lời:

– Với $x = 0$ giờ $⇒ y = 2.0 + 3 = 3 (m^3)$;

– Với $x = 1$ giờ $⇒ y = 2.1 + 3 = 5 (m^3)$;

– Với $x = 2$ giờ $⇒ y = 2.2 + 3 = 7 (m^3)$;

– Với $x = 3$ giờ $⇒ y = 2.3 + 3 = 9 (m^3)$;

– Với $x = 10$ giờ $⇒ y = 2.10 + 3 = 23 (m^3)$.

Ta có bảng sau

$x$	0	1	2	3	10
$y = f(x) = 2x + 3$	3	5	7	9	23

Thực hành 2 trang 17 Toán 8 tập 2 CTST

Lập bảng giá trị của mỗi hàm số bậc nhất sau:

$y = f(x) = 4x – 1$ và $y = h(x) = – 0,5x + 8$ với $x$ lần lượt bằng $–3; –2; –1; 0; 1; 2; 3$.

Trả lời:

– Với $x = – 3$

$⇒ f( – 3) = 4.( – 3) – 1 = – 13$

$⇒ g( – 3) = – 0,5.( – 3) + 8 = 9,5$

– Với $x = – 2$

$⇒ f( – 2) = 4.( – 2) – 1 = – 9

$⇒ g( – 2) = – 0,5.( – 2) + 8 = 9$

– Với $x = – 1$

$⇒ f( – 1) = 4.( – 1) – 1 = – 5$

$⇒ g( – 1) = – 0,5.( – 1) + 8 = 8,5$

– Với $x = 0$

$⇒ f(0) = 4.0 – 1 = – 1$

$⇒ g(0) = – 0,5.0 + 8 = 8$

– Với $x = 1$

$⇒ f(1) = 4.1 – 1 = 3$

$⇒ g(1) = – 0,5.1 + 8 = 7,5$

– Với $x = 2$

$⇒ f(2) = 4.2 – 1 = 7$

$⇒ g(2) = – 0,5.2 + 8 = 7$

– Với $x = 3$

$⇒ f(3) = 4.3 – 1 = 11$

$⇒ g(3) = – 0,5.3 + 8 = 6,5$

Ta có bảng sau:

$x$	–3	–2	–1	0	1	2	3
$y = f(x) = 4x – 1$	–13	–9	–5	–1	3	7	11
$y = g(x) = – 0,5x + 8$	9,5	9	8,5	8	7,5	7	6,5

Vận dụng 2 trang 17 Toán 8 tập 2 CTST

Một xe khách khởi hành từ bến xe phía Bắc bưu điện thành phố Nha Trang để đi ra thành phố Đà Nẵng với tốc độ $40$ km/h (Hình 2).

a) Biết rằng bến xe cách bưu điện thành phố Nha Trang $6$ km. Sau $x$ giờ, xe khách cách bưu điện thành phố Nha Trang $y$ km. Tính $y$ theo $x$.

b) Chứng minh rằng $y$ là một hàm số bậc nhất theo biến $x$.

c) Hoàn thành bảng giá trị của hàm số ở câu b) và giải thích ý nghĩa của bảng giá trị này:

$x$	0	1	2	3
$y$	?	?	?	?

Trả lời:

a) Quãng đường xe khách đi được sau $x$ giờ với vận tốc $40$ km/h là $40.x$ (km)

Vì ban đầu bến xe cách bưu điện Nha Trang $6$ km nên sau $x$ giờ xe khách cách bưu điện thành phố Nha Trang số km là: $40x + 6$.

Do đó, $y = 40x + 6$ với $y$ là số km xe khách cách bưu điện thành phố Nha Trang sau $x$ giờ.

b) Vì hàm số $y = 40x + 6$ có dạng $y = ax + b$ với $a = 40;b = 6$ nên $y$ là một hàm số bậc nhất theo biến $x$.

c) Ta có:

– Với $x = 0 ⇒ y = f(0) = 40.0 + 6 = 6$;

– Với $x = 1 ⇒ y = f(1) = 40.1 + 6 = 46$;

– Với $x = 2 ⇒ y = f(2) = 40.2 + 6 = 86$;

– Với $x = 3 ⇒ y = f(3) = 40.3 + 6 = 126$;

Ta có bảng giá trị sau:

$x$	0	1	2	3
$y$	6	46	86	126

Bảng này thể hiện khoảng cách của xe khách so với bưu điện Nha Trang sau $0$ giờ; $1$ giờ; $2$ giờ; $3$ giờ.

– Tại điểm khởi hành, xe khách cách bưu điện thành phố Nha Trang $6$ km.

– Sau khi đi được $1$ giờ xe khách cách bưu điện thành phố Nha Trang $46$ km.

– Sau khi đi được $2$ giờ xe khách cách bưu điện thành phố Nha Trang $86$ km.

– Sau khi đi được $3$ giờ xe khách cách bưu điện thành phố Nha Trang $126$ km.

3. ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT

Hoạt động khám phá 3 trang 18 Toán 8 tập 2 CTST

Hùng mua $x$ mét dây điện và phải trả số tiền là $y$ nghìn đồng. Giá trị tương ứng giữa $x$ và $y$ được cho bởi bảng sau:

$x$	1	2	3	4
$y$	4	8	12	16

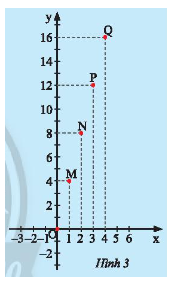
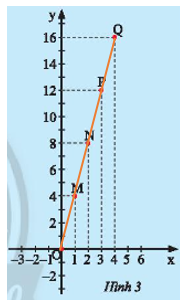
Hùng vẽ các điểm $M(1;4); N(2;8); P(3;12); Q(4;16)$ trên mặt phẳng tọa độ $Oxy$ như Hình 3. Hãy dùng thước thẳng để kiểm tra các điểm $O;M;N;P;Q$ có thẳng hàng không.

Trả lời:

Dùng thước thẳng kiểm tra ta thấy các điểm $O;M;N;P;Q$ thẳng hàng.

Thực hành 3 trang 20 Toán 8 tập 2 CTST

a) Vẽ đồ thị của hàm số: $y = 0,5x; \,y = – 3x; \, y = x$.

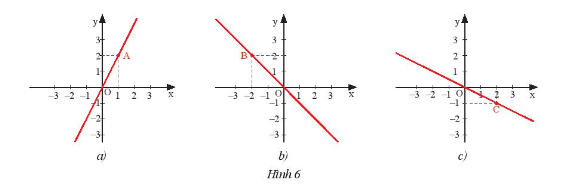
b) Các đồ thị sau đây là đồ thị của hàm số nào?

Trả lời:

a) ♦ Vẽ đồ thị hàm số $y = 0,5x$

Cho $x = 1 ⇒ y = 0,5.1 = 0,5$. Ta vẽ điểm $A(1;0,5)$

Đồ thị hàm số $y = 0,5x$ là đường thẳng đi qua điểm $O(0;0)$ và $A(1;0,5)$.

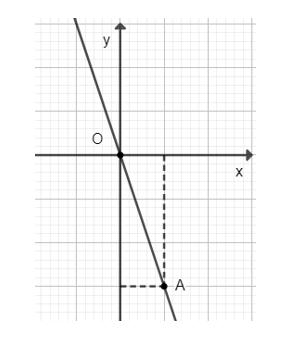
♦ Vẽ đồ thị hàm số $y = – 3x$

Cho $x = 1 ⇒ y = – 3.1 = – 3$. Ta vẽ điểm $A(1; – 3)$

Đồ thị hàm số $y = – 3x$ là đường thẳng đi qua điểm $O(0;0)$ và $A(1; – 3)$.

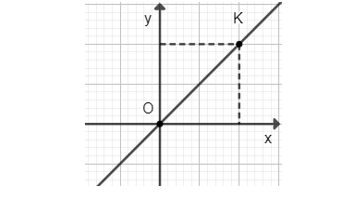
♦ Vẽ đồ thị hàm số $y = x$

Cho $x = 1 ⇒ y = 1$. Ta vẽ điểm $K(1;1)$

Đồ thị hàm số $y = x$ là đường thẳng đi qua điểm $O(0;0)$ và $K(1;1)$.

b) Ta thấy cả ba đồ thị đều đi qua gốc tọa độ $O(0;0)$ nên có dạng $y = ax$.

– Ở đồ thị hình 6a), đồ thị hàm số đi qua điểm $A(1;2)$ nên ta có:

$2 = a.1 ⇒ a = 2$.

Do đó, đồ thị hình 6a) là đồ thị của hàm số $y = 2x$.

– Ở đồ thị hình 6b), đồ thị hàm số đi qua điểm $B( – 2;2)$ nên ta có:

$2 = a.(- 2) ⇒ a = 2:(- 2) = – 1$.

Do đó, đồ thị hình 6b) là đồ thị của hàm số $y = – x$.

– Ở đồ thị hình 6c), đồ thị hàm số đi qua điểm $C(2; – 1)$ nên ta có:

$ – 1 = a.2 ⇒ a = (- 1):2 = \dfrac{-1}{2}$.

Do đó, đồ thị hình 6c) là đồ thị của hàm số $y = \dfrac{- 1}{2}x$.

Hoạt động khám phá 4 trang 20 Toán 8 tập 2 CTST

Cho hàm số $y = f(x) = x$ và $y = g(x) = x + 3$.

a) Thay dấu ? bằng số thích hợp.

$x$	–2	–1	0	1	2
$y = f(x) = x$	?	?	?	?	?
$y = g(x) = x + 3$	?	?	?	?	?

b) Trên cùng một mặt phẳng tọa độ, vẽ đồ thị của hàm số $y = f(x)$ và biểu diễn các điểm có tọa độ thỏa mãn hàm số $y = g(x)$ có trong bảng trên.

c) Kiểm tra xem các điểm thuộc đồ thị hàm số của $y = g(x)$ vẽ ở câu b có thẳng hàng không. Và dự đoán cách vẽ đồ thị hàm số $y = g(x)$.

Trả lời:

a) Ta có:

– Với $x = – 2 ⇒ f( – 2) = – 2; \,g(- 2) = – 2 + 3 = 1$;

– Với $x = – 1 ⇒ f( – 1) = – 1; \,g(- 1) = – 1 + 3 = 2$;

– Với $x = 0 ⇒ f(0) = 0; \,g(0) = 0 + 3 = 3$;

– Với $x = 1 ⇒ f(1) = 1; \,g(1) = 1 + 3 = 4$;

– Với $x = 2 ⇒ f(2) = 2; \,g(2) = 2 + 3 = 5$;

Ta có bảng sau:

$x$	–2	–1	0	1	2
$y = f(x) = x$	–2	–1	0	1	2
$y = g(x) = x + 3$	1	2	3	4	5

b) – Vẽ đồ thị hàm số $y = f(x) = x$

Cho $x = 1 ⇒ y = f(x) = 1$. Ta vẽ điểm $A(1;1)$

Đồ thị hàm số $y = x$ là đường thẳng đi qua điểm $O(0;0)$ và $A(1;1)$.

– Các điểm có tọa độ thỏa mãn hàm số $y = g(x)$ trong bảng trên là $B( – 2;1); C( – 1;2); D(0;3); E(1;4); F(2;5)$.

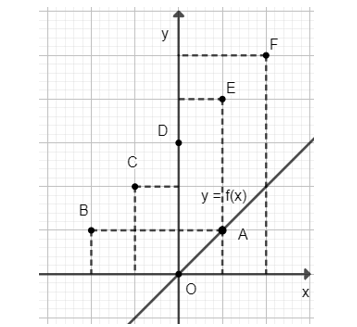
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số $y = g(x) = x = 3$ thẳng hàng với nhau.

Dự đoán cách vẽ đồ thị hàm số $y = g(x)$:

Bước 1: Chọn hai điểm $A;B$ phân biệt thuộc đồ thị hàm số $y = g(x)$.

Bước 2: Vẽ đường thẳng đi qua hai điểm $A;B$.

Đồ thị hàm số $y = g(x)$ là đường thẳng đi qua hai điểm $A;B$.

Thực hành 4 trang 21 Toán 8 tập 2 CTST

Vẽ đồ thị của các hàm số sau:

a) $y = 5x + 2$;

b) $y = – 2x – 6$.

Trả lời:

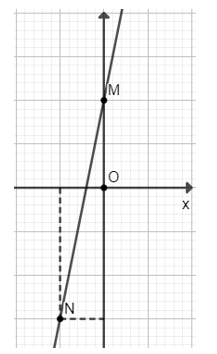
a) Vẽ đồ thị hàm số $y = 5x + 2$;

Cho $x = 0 ⇒ y = 2$ ta được điểm $M(0;2)$ trên trục $Oy$

Cho $x = -1 ⇒ y = -3$ ta được điểm $N(-1;-3)$

Vẽ đường thẳng đi qua hai điểm $M;N$ ta được đồ thị của hàm số $y = 5x + 2$.

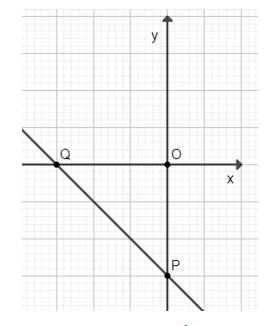
b) Vẽ đồ thị hàm số $y = – 2x – 6$

Cho $x = 0 ⇒ y = – 6$ ta được điểm $P(0; – 6)$ trên trục $Oy$.

Cho $y = 0 ⇒ x = – 3$ ta được điểm $Q( – 3;0)$ trên $Ox$.

Vẽ đường thẳng đi qua hai điểm $P;Q$ ta được đồ thị của hàm số $y = – 2x – 6$.

Vận dụng 3 trang 21 Toán 8 tập 2 CTST

Một lò xo có chiều dài ban đầu khi chưa treo vật nặng là $10$ cm. Cho biết treo thêm vào lò xo một vật nặng $1$ kg thì chiều dài lò xo tăng thêm $3$ cm.

a) Tính chiều dài $y$ (cm) của lò xo theo khối lượng $x$ (kg) của vật.

b) Vẽ đồ thị của hàm số $y$ theo biến số $x$.

Trả lời:

a) Vì cứ treo thêm $1$ kg vật nặng thì lò xo dài thêm $3$ cm nên treo thêm $x$ kg vật nặng thì lò xo dài thêm $3x$ cm.

Chiều dài của lò xo sau khi treo vật nặng là:

$y = 3x + 10$.

b) Vẽ đồ thị hàm số $y = 3x + 10$

Cho $x = -3 ⇒ y = 1$ ta được điểm $A(-3;1)$

Cho $x = -2 ⇒ y = 4$ ta được điểm $B(-2;4)$

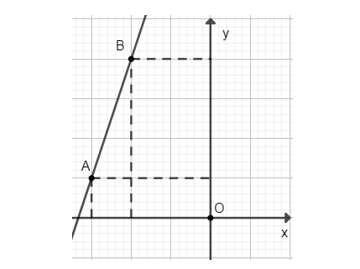
Đồ thị hàm số $y = 3x + 10$ là đường thẳng đi qua hai điểm $A;B$.

GIẢI BÀI TẬP

Sau đây là phần Giải bài 1 2 3 4 5 6 trang 22 sgk Toán 8 tập 2 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 trang 22 Toán 8 tập 2 CTST

Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số $a, \,b$ của chúng.

a) $y = 4x + 2$;

b) $y = 5 – 3x$;

c) $y = 2 + {x^2}$;

d) $y = – 0,2x$;

e) $y = \sqrt 5 x – 1$.

Bài giải:

a) Hàm số $y = 4x + 2$ là hàm số bậc nhất vì có dạng $y = ax + b$ với $a,b$ là các số cho trước và $a \ne 0$. Ta có, $a = 4;b = 2$.

b) Hàm số $y = 5 – 3x = – 3x + 5$ là hàm số bậc nhất vì có dạng $y = ax + b$ với $a,b$ là các số cho trước và $a \ne 0$. Ta có, $a = – 3;b = 5$.

c) Hàm số $y = 2 + {x^2}$ không phải là hàm số bậc nhất vì không có dạng $y = ax + b$ với $a,b$ là các số cho trước và $a \ne 0$.

d) Hàm số $y = – 0,2x$ là hàm số bậc nhất vì có dạng $y = ax + b$ với $a,b$ là các số cho trước và $a \ne 0$. Ta có, $a = – 0,2;b = 0$.

e) Hàm số $y = \sqrt 5 x – 1$ là hàm số bậc nhất vì có dạng $y = ax + b$ với $a,b$ là các số cho trước và $a \ne 0$. Ta có, $a = \sqrt 5 ;b = – 1$.

Giải bài 2 trang 22 Toán 8 tập 2 CTST

Với giá trị nào của $m$ thì mỗi hàm số sau đây là hàm số bậc nhất?

a) $y = (m – 1)x + m$;

b) $y = 3 – 2mx$.

Bài giải:

a) Để hàm số $y = (m – 1)x + m$ là hàm số bậc nhất thì $m – 1 \ne 0 \Leftrightarrow m \ne 1$.

Vậy để hàm số $y = (m – 1)x + m$ là hàm số bậc nhất thì $m \ne 1$.

b) Ta có: $y = 3 – 2mx = – 2mx + 3$

Để hàm số $y = – 2mx + 3$ là hàm số bậc nhất thì $ – 2m \ne 0 \Leftrightarrow m \ne 0$.

Vậy để hàm số $y = 3 – 2mx$ là hàm số bậc nhất thì $m \ne 0$.

Giải bài 3 trang 22 Toán 8 tập 2 CTST

a) Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:

$y = x$; $y = x + 2$; $y = – x$; $y = – x + 2$.

b) Bốn đồ thị nói trên cắt nhau tại các điểm $O(0;0), A, B, C$. Tứ giác có bốn đỉnh $O; A; B; C$ là hình gì? Giải thích.

Bài giải:

a) ♦ Vẽ đồ thị hàm số $y = x$

Cho $x = 1 ⇒ y = 1$ ⇒ đồ thị hàm số đi qua điểm $C(1;1)$.

Đồ thị hàm số $y = x$ là đường thẳng đi qua hai điểm $O(0;0)$ và $C(1;1)$.

♦ Vẽ đồ thị hàm số $y = x + 2$

Cho $x = 0 ⇒ y = 2$ ta được điểm $B(0;2)$ trên trục $Oy$.

Cho $x = -1 ⇒ y = 1$ ta được điểm $A( – 1;1)$

Đồ thị hàm số $y = x + 2$ là đường thẳng đi qua hai điểm $A(-1;1)$ và $B(0;2)$.

♦ Vẽ đồ thị hàm số $y = – x$

Cho $x = -1 ⇒ y = 1$ ⇒ đồ thị hàm số đi qua điểm $A(-1;1)$.

Đồ thị hàm số $y = – x$ là đường thẳng đi qua hai điểm $O(0;0)$ và $A(-1;1)$.

♦ Vẽ đồ thị hàm số $y = – x + 2$

Cho $x = 0 ⇒ y = 2$ ta được điểm $B(0;2)$ trên trục $Oy$.

Cho $x = 1 ⇒ y = 1$ ta được điểm $C(1;1)$.

Đồ thị hàm số $y = – x + 2$ là đường thẳng đi qua hai điểm $B(0;2)$ và $C(1;1)$.

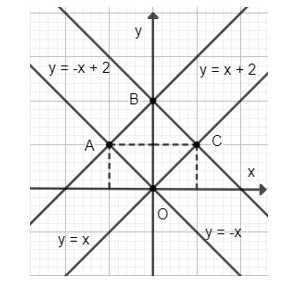
b) Vì đường thẳng $y = x$;$y = x + 2$ song song với nhau và $y = – x$;$y = – x + 2$ song song với nhau nên tứ giác $OABC$ là hình bình hành.

Lại có $OC;OA$ là đường chéo của hình vuông có độ dài cạnh là 1 nên $OC = OA$. Do đó, tứ giác $OABC$ là hình thoi.

Lại có $OC;OA$ là đường chéo của hình vuông nên cũng là đường phân giác. Do đó:

$\widehat {COB} = \widehat {AOB} = 45^\circ$

$⇒ \widehat {COA} = \widehat {COB} + \widehat {AOB} = 45^\circ + 45^\circ = 90^\circ$

Hình thoi $OABC$ có góc $\widehat {COA} = 90^\circ $ nên tứ giác $OABC$ là hình vuông.

Hoặc:

b) Ta có:

Đường thẳng $y = x$ song song với đường thẳng $y = x + 2$ suy ra $OC // AB$.

Đường thẳng $y = −x$ song song với đường thẳng $y = −x + 2$ suy ra $OA // BC$.

Tứ giác $OABC$ có: $OC // AB, OA // BC$

Suy ra tứ giác $OABC$ là hình bình hành.

Hình bình hành $OABC$ có hai đường chéo $OB$ và $AC$ vuông góc và bằng nhau nên tứ giác $OABC$ là hình vuông.

Giải bài 4 trang 22 Toán 8 tập 2 CTST

Để đổi nhiệt độ từ $F$ (Fahrenheit) sang độ $C$ (Celsius), ta dùng công thức $C = \dfrac{5}{9}.(F – 32)$.

a) $C$ có phải hàm số bậc nhất theo biến số $F$ không?

b) Hãy tính $C$ khi $F = 32$ và tính $F$ khi $C = 100$.

Bài giải:

a) Ta có:

$C = \dfrac{5}{9}.(F – 32) = \dfrac{5}{9}F – \dfrac{5}{9}.32 = \dfrac{5}{9}F – \dfrac{{160}}{9}$

Vì $C = \dfrac{5}{9}F – \dfrac{{160}}{9}$ có dạng $C = aF – b$ với $a = \dfrac{5}{9}$ và $b = – \dfrac{{160}}{9}$ nên $C$ là hàm số bậc nhất của biến số $F$.

b) – Với $F = 32 ⇒ C = \dfrac{5}{9}.32 – \dfrac{{160}}{9} = \dfrac{{160}}{9} – \dfrac{{160}}{9} = 0$

Vậy với $F = 32$ thì $C = 0$.

– Với $C = 100 ⇒ 100 = \dfrac{5}{9}F – \dfrac{{160}}{9}$

$⇔ \dfrac{5}{9}F = 100 + \dfrac{{160}}{9}$

$⇔ \dfrac{5}{9}F = \dfrac{{1060}}{9}$

$⇔ F = \dfrac{{1060}}{9}:\dfrac{5}{9}$

$⇒ F = 212$

Vậy khi $C = 100$ thì $F = 212$.

Giải bài 5 trang 22 Toán 8 tập 2 CTST

Gọi $C$ và $r$ lần lượt là chu vi và bán kính của một đường tròn. Hãy chứng tỏ $C$ là một hàm số bậc nhất theo biến số $r$. Tìm hệ số $a, b$ của hàm số này.

Bài giải:

Công thức tính chu vi đường tròn:

$C = \pi .d = \pi .2r$ (đơn vị độ dài)

Trong đó, $C$ là chu vi đường tròn; $r$ là bán kính đường tròn; $d$ là đường kính đường tròn.

Vì $C = 2\pi .r$ nên $C$ là hàm số bậc nhất theo biến $r$ vì có dạng $C = a.r + b$.

Ta có: $C = 2\pi .r$ nên $a = 2\pi ;b = 0$.

Vậy $C$ là một hàm số bậc nhất theo biến $r$ với $a = 2\pi ;b = 0$.

Giải bài 6 trang 22 Toán 8 tập 2 CTST

Một người đi bộ trên đường thẳng với tốc độ $v \,(km/h)$. Gọi $s \,(km)$ là quãng đường đi được trong $t \,(h)$.

a) Lập công thức tính $s$ theo $t$.

b) Vẽ đồ thị của hàm số $s$ theo $t$ khi $v = 4$.

Bài giải:

a) Cứ $1$ giờ người đó lại đi được $v$ km.

Cứ $2$ giờ người đó lại đi được $2v$ km.

Vậy sau $t \,(h)$ người đó sẽ đi được quãng đường $v.t$ km.

Vậy ta có công thức tính $s$ theo $t$ như sau: $s = v.t$ trong đó $v$ là vận tốc, $t$ là thời gian và $s$ là quãng đường đi được.

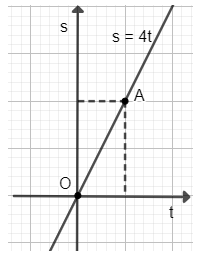
b) Với $v = 4 ⇒ s = 4t$. Khi đó $s$ là hàm số bậc nhất theo biến $t$.

Với $t = 1 ⇒ s = 4.1 = 4 ⇒ $ đồ thị hàm số đi qua điểm $A(1;4)$.

Đồ thị hàm số $s = 4t$ là đường thẳng đi qua hai điểm $O(0;0)$ và $A(1;4)$.

Bài trước:

👉 Giải bài 1 2 3 4 5 6 7 8 trang 14 sgk Toán 8 tập 2 Chân Trời Sáng Tạo

Bài tiếp theo:

👉 Giải bài 1 2 3 4 5 6 7 8 9 10 trang 26 27 sgk Toán 8 tập 2 Chân Trời Sáng Tạo

Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 trang 22 sgk Toán 8 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“

\(x\)	–2	–1	0	1	2
\(y = f(x) = x\)	?	?	?	?	?
\(y = g(x) = x + 3\)	?	?	?	?	?

\(x\)	0	1	2	3
\(y\)	?	?	?	?

\(x\)	1	2	3	4
\(y\)	4	8	12	16