Nội Dung
Hướng dẫn giải Bài 4. Phép nhân và phép chia đa thức một biến sgk Toán 7 tập 2 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 5 6 trang 40 sgk Toán 7 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
BÀI 4. PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC MỘT BIẾN
Hoạt động khởi động trang 37 Toán 7 tập 2 CTST
Có thể nhân, chia hai đa thức một biến được không?
Trả lời:
Ta có thể thực hiện nhân, chia hai đa thức một biến.
1. PHÉP NHÂN ĐA THỨC MỘT BIẾN
Hoạt động khám phá 1 trang 37 Toán 7 tập 2 CTST
Hãy dùng tính chất phân phối để thực hiện phép nhân $x.(2x+3)$.
Trả lời:
Ta có:
$x.(2x + 3) = x.2x + 3.x = 2{x^2} + 3x$
Thực hành 1 trang 37 Toán 7 tập 2 CTST
Thực hiện phép nhân \((4x – 3)(2{x^2} + 5x – 6)\).
Trả lời:
Ta thực hiện như sau:
$(4x – 3)(2{x^2} + 5x – 6)$
$= 4x.2{x^2} + 4x.5x – 6.4x – 3.2{x^2} – 3.5x + 18$
$= 8{x^3} + 20{x^2} – 6{x^2} – 24x – 15x + 18$
$= 8{x^3} + 14{x^2} – 39x + 18$
Vận dụng 1 trang 37 Toán 7 tập 2 CTST
Tìm đa thức theo biến $x$ biểu thị thể tích của hình hộp chữ nhật có kích thước như Hình 2.
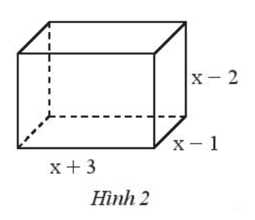
Trả lời:
Thể tích hình hộp chữ nhật là:
$(x + 3).(x – 1).(x – 2)$
$= \left[ {(x + 3).(x – 1)} \right].(x – 2)$
$= (x.x – 1.x + 3.x – 3.1)(x – 2)$
$= ({x^2} + 2x – 3)(x – 2)$
$= {x^2}.x – 2.{x^2} + 2x.x – 2x.2 – 3.x + 3.2$
$= {x^3} – 7x + 6$
Vậy đa thức biểu thị thể tích của hình hộp chữ nhật trên là ${x^3} – 7x + 6$.
2. PHÉP CHIA ĐA THỨC MỘT BIẾN
Hoạt động khám phá 2 trang 38 Toán 7 tập 2 CTST
Thực hiện phép nhân \((3x + 1)({x^2} – 2x + 1)\), rồi đoán xem \((3{x^3} – 5{x^2} + x + 1) : (3x + 1)\) bằng đa thức nào.
Trả lời:
Ta có:
$(3x + 1)({x^2} – 2x + 1)$
$= 3x({x^2} – 2x + 1) + 1({x^2} – 2x + 1)$
$= 3{x^3} – 6{x^2} + 3x + {x^2} – 2x + 1$
$= 3{x^3} – 5{x^2} + x + 1$
Vì \((3x + 1)({x^2} – 2x + 1) = 3{x^3} – 5{x^2} + x + 1\)
\(⇒ (3{x^3} – 5{x^2} + x + 1) : (3x + 1) = {x^2} – 2x + 1\)
Thực hành 2 trang 38 Toán 7 tập 2 CTST
Thực hiện phép chia \(P(x) = (6{x^2} + 4x)\) cho $Q(x) = 2x$.
Trả lời:
Ta có:
\((6{x^2} + 4x) : 2x = (6{x^2}:2x) + (4x:2x) = 3x + 2\)
Vậy $P(x) : Q(x) = 3x + 2$.
Vận dụng 2 trang 39 Toán 7 tập 2 CTST
Thực hiện các phép chia sau \(\frac{9{x^2} + 5x + x}{3x}\) và \(\frac{(2{x^2} – 4x) + (x – 2)}{2 – x}\).
Trả lời:
Ta chia lần lượt theo công thức đã cho, phải thu gọn các đa thức trong phép chia và xếp thứ tự lũy thừa giảm dần của biến.
• Ta có:
\(\frac{9{x^2} + 5x + x}{3x} = \frac{9{x^2} + 6x}{3x} = \frac{9x^2}{3x} + \frac{6x}{3x} = 3x + 2\)
Vậy \(\frac{9{x^2} + 5x + x}{3x} = 3x + 2\).
• Ta có:
\(\frac{2{x^2} – 3x – 2}{2 – x} = \frac{2x^2 – 3x – 2}{- x + 2} = \frac{2x^2 – 4x}{- x + 2} + \frac{x – 2}{ – x + 2} =- 2x – 1\)
Vậy \(\frac{(2{x^2} – 4x) + (x – 2)}{2 – x} = – 2x – 1\).
Thực hành 3 trang 39 Toán 7 tập 2 CTST
Thực hiện phép chia \((x^2 + 5x + 9):(x + 2)\).
Trả lời:
Ta có thể thực hiện theo 2 cách như sau:
♦ Cách 1:
$(x^2 + 5x + 9):(x + 2) = \frac{x^2 + 5x + 9}{x + 2}$
$= \frac{(x +3)(x + 2) + 3}{x + 2}$
$= \frac{(x +3)(x + 2)}{x + 2} + \frac{3}{x + 2}$
$= (x + 3) + \frac{3}{{x + 2}}$
♦ Cách 2: đặt tính
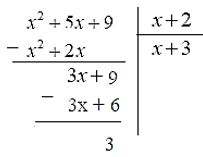
Vậy \((x^2 + 5x + 9):(x + 2) = x + 3 + \frac{3}{x + 2}\)
Hay $(x^2 + 5x + 9) = (x + 2).(x + 3) + 3$.
Vận dụng 3 trang 39 Toán 7 tập 2 CTST
Tính diện tích đáy của một hình hộp chữ nhật (Hình 3) có chiều cao bằng $(x + 3)$ cm và có thể tích bằng \(({x^3} + 8{x^2} + 19x + 12) \,cm^3\).
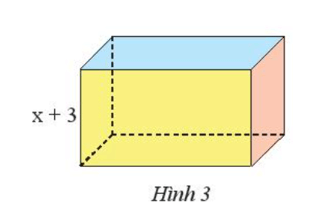
Trả lời:
Thể tích hình hộp chữ nhật bằng diện tích đáy nhân với chiều cao.
Do đó diện tích đáy hình hộp là:
$({x^3} + 8{x^2} + 19x + 12):(x + 3)$
Thực hiện đặt phép chia ta được:
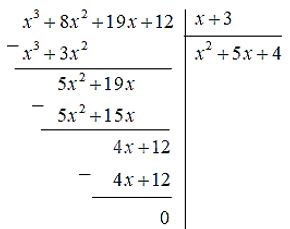
Vậy diện tích đáy của hình hộp chữ nhật bằng \(x^2 + 5x + 4 \,cm^2\).
3. TÍNH CHẤT CỦA PHÉP NHÂN ĐA THỨC MỘT BIẾN
Thực hành 4 trang 40 Toán 7 tập 2 CTST
Thực hiện phép tính \(\dfrac{1}{5}.({x^2} + 1).5\).
Trả lời:
Ta thực hiện như sau:
$\dfrac{1}{5}({x^2} + 1).5 = \dfrac{1}{5}.5.({x^2} + 1)$
$= (\dfrac{1}{5}.5).{x^2} + 1 = 1. ({x^2} + 1)$
$= {x^2} + 1$
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 trang 40 sgk Toán 7 tập 2 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 40 Toán 7 tập 2 CTST
Thực hiện phép nhân.
a) \((4x – 3)(x + 2)\);
b) \((5x + 2)( – {x^2} + 3x + 1)\);
c) \((2{x^2} – 7x + 4)( – 3{x^2} + 6x + 5)\).
Bài giải:
a) Ta có:
$(4x – 3)(x + 2)$
$= 4x(x + 2) – 3(x + 2)$
$= 4{x^2} + 8x – 3x – 6$
\(= 4{x^2} + 5x – 6\)
b) Ta có:
\((5x + 2)( – {x^2} + 3x + 1)\)
\(= 5x( – {x^2} + 3x + 1) + 2( – {x^2} + 3x + 1)\)
\(= – 5{x^3} + 15{x^2} + 5x – 2{x^2} + 6x + 2\)
\(= – 5{x^3} + 13{x^2} + 11x + 2\)
c) Ta có:
\((2{x^2} – 7x + 4)(- 3{x^2} + 6x + 5)\)
\(= 2{x^2}( – 3{x^2} + 6x + 5) – 7x(- 3{x^2} + 6x + 5) + 4(- 3{x^2} + 6x + 5)\)
\(= 2{x^2}(- 3{x^2}) + 2{x^2}.6x + 2{x^2}.5 + 7x.3{x^2} – 7x.6x – 7x.5 + 4(- 3{x^2}) + 4.6x + 4.5\)
\(= – 6{x^4} + 33{x^3} – 44{x^2} – 11x + 20\)
Giải bài 2 trang 40 Toán 7 tập 2 CTST
Cho hai hình chữ nhật như Hình 4. Tìm đa thức theo biến $x$ biểu thị diện tích của phần được tô màu xanh.
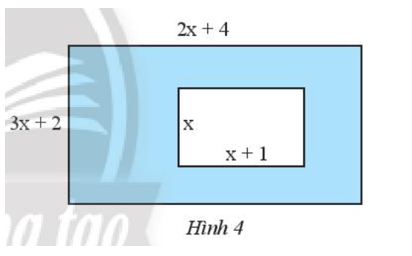
Bài giải:
Ta có:
Diện tích hình chữ nhật to bên ngoài là:
$(2x + 4)(3x + 2) = 2x + 4(3x + 2)$
$= 6x^2 + 4x + 12x + 8$
$= 6x^2 + 16x + 8$
Diện tích hình chữ nhật nhỏ bên trong là:
\(x(x + 1) = {x^2} + x\)
⇒ Diện tích phần cần tìm là:
$6x^2 + 16x + 8 – x^2 – x$
$= 5x^2 + 15x + 8$
Vậy biểu thức biểu thị diện tích của phần được tô màu xanh là $5x^2 + 15x + 8$.
Giải bài 3 trang 40 Toán 7 tập 2 CTST
Thực hiện phép chia.
a) \((8{x^6} – 4{x^5} + 12{x^4} – 20{x^3}):4{x^3}\);
b) \((2{x^2} – 5x + 3):(2x – 3)\).
Bài giải:
a) Ta thực hiện như sau:
\((8{x^6} – 4{x^5} + 12{x^4} – 20{x^3}):4{x^3}\)
\(= (8{x^6}:4{x^3}) – (4{x^5}:4{x^3}) + (12{x^4}:4{x^3}) – (20{x^3}:4{x^3})\)
\(= 2{x^2} – {x^2} + 3x – 5\)
Vậy \((8{x^6} – 4{x^5} + 12{x^4} – 20{x^3}):4{x^3} = 2{x^2} – {x^2} + 3x – 5\).
b) Thực hiện đặt phép chia ta được:
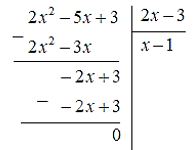
Vậy \((2{x^2} – 5x + 3):(2x – 3)= x – 1\).
Giải bài 4 trang 40 Toán 7 tập 2 CTST
Thực hiện phép chia.
a) \((4x^2 – 5):(x – 2)\);
b) \((3x^3 – 7x + 2):(2x^2 – 3)\).
Bài giải:
a) Ta có:
$(4x^2 – 5):(x – 2) = \dfrac{4x^2 – 5}{x – 2}$
Thực hiện đặt phép chia ta được:
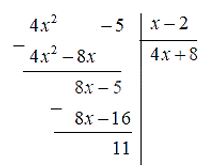
Vậy \((4{x^2} – 5):(x – 2)= 4x + 8 + \dfrac{11}{x – 2}\).
Hay \((4{x^2} – 5) = (4x + 8).(x – 2) + 11\).
b) Ta có:
\((3x^3 – 7x + 2):(2x^2 – 3) = \dfrac{3x^3 – 7x + 2}{2x^2 – 3}\)
Thực hiện đặt phép chia ta được:

Vậy \((3x^3 – 7x + 2):(2x^2 – 3) = \dfrac{3}{2}x + \dfrac{-\dfrac{5}{2}x – 2}{2x^2 – 3}\).
Hay \((3x^3 – 7x + 2) = \dfrac{3}{2}x.(2x^2 – 3) – \dfrac{5}{2}x + 2\).
Giải bài 5 trang 40 Toán 7 tập 2 CTST
Tính chiều dài của một hình chữ nhật có diện tích bằng \((4{y^2} + 4y – 3) \,cm^2\) và chiều rộng bằng $(2y – 1) \,cm$.
Bài giải:
Diện tích hình chữ nhật = chiều dài . chiều rộng
Do đó chiều dài hình chữ nhật bằng:
\((4{y^2} + 4y – 3):(2y – 1) = \dfrac{{4{y^2} + 4y – 3}}{{2y – 1}}\)
Thực hiện đặt phép chia ta được:

Vậy chiều dài hình chữ nhật là $2y + 3 \,cm$.
Giải bài 6 trang 40 Toán 7 tập 2 CTST
Cho hình hộp chữ nhật có thể tích bằng (\(3{x^3} + 8{x^2} – 45x – 50) \,cm^3\), chiều dài bằng $(x + 5) \,cm$ và chiều cao bằng $(x + 1) \,cm$. Hãy tính chiều rộng của hình hộp chữ nhật đó.
Bài giải:
Ta có thể tích hình hộp chữ nhật bằng tích chiều cao và diện tích đáy
Nên chiều rộng của hình chữ nhật = thể tích : (chiều cao . chiều dài )
Diện tích đáy là \((x + 5)(x + 1) = {x^2} + 6x + 5\)
Thay các số ở đề bài cho vào công thức trên ta được:
\(\dfrac{3x^3 + 8x^2 – 45x – 50}{x^2 + 6x + 5}\)
Thực hiện đặt phép chia ta được:
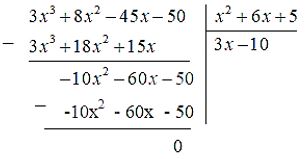
Vậy chiều dài hình hộp chữ nhật là $3x – 10 \,cm$.
Bài trước:
👉 Giải bài 1 2 3 4 5 6 7 8 9 trang 35 36 sgk Toán 7 tập 2 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 HĐTH&TN: Cách tính điểm trung bình môn học kì Toán 7 tập 2 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 trang 40 sgk Toán 7 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
