Nội Dung
Hướng dẫn giải Bài §10. Số nguyên tố. Hợp số sgk Toán 6 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 6 trang 42 43 sgk Toán 6 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 6.
§10. SỐ NGUYÊN TỐ. HỢP SỐ
Câu hỏi khởi động trang 41 Toán 6 tập 1 CD
Bác Vĩnh mua 17 cuốn sổ và 34 chiếc bút để làm quà tặng. Bác Vĩnh muốn chia đều 17 cuốn sổ thành các gói và cũng muốn chia đều 34 chiếc bút thành các gói.
Bác Vĩnh có bao nhiêu cách chia những cuốn sổ thành các gói? Có bao nhiêu cách chia những chiếc bút thành các gói?
Trả lời:
– Để tìm số cách chia những cuốn sổ thành các gói đều nhau, ta tìm các ước của 17 bằng cách lần lượt thực hiện phép chia 17 cho các số tự nhiên từ 1 đến 17, các phép chia hết là:
17 : 1 = 17 và 17 : 17 = 1
Vậy có 2 cách chia những cuốn sách thành các gói đều nhau:
+ Cách 1: Để 1 gói gồm 17 cuốn
+ Cách 2: Chia làm 17 gói, mỗi gói 1 cuốn sổ.
– Để tìm số cách chia những chiếc bút bi thành các gói đều nhau, ta tìm ước của 34 bằng cách thực hiện phép chia 34 cho các số tự nhiên từ 1 đến 34, các phép chia hết là:
34 : 1 = 34; 34 : 2 = 17; 34 : 17 = 2; 34 : 34 = 1
Vậy có 4 cách chia những chiếc bút thành các gói đều nhau:
+ Cách 1: Chia thành 1 gói 34 chiếc.
+ Cách 2: Chia thành 2 gói, mỗi gói 17 chiếc.
+ Cách 3: Chia thành 17 gói, mỗi gói 2 chiếc.
+ Cách 4: Chia thành 34 gói, mỗi gói 1 chiếc.
Hoạt động trang 41 Toán 6 tập 1 CD
a) Tìm các ước của mỗi số sau: 2, 3, 4, 5, 6, 7, 17, 34.
b) Trong các số trên, những số nào có hai ước, những số nào có nhiều hơn hai ước?
Trả lời:
a) Các ước của 2 là: 1; 2
Các ước của 3 là: 1; 3
Các ước của 4 là: 1; 2; 4
Các ước của 5 là: 1; 5
Các ước của 6 là: 1; 2; 3; 6
Các ước của 7 là: 1; 7
Các ước của 17 là: 1; 17
Các ước của 34 là: 1; 2; 17; 34.
b) Các số 2, 3, 5, 7, 17 chỉ có hai ước là 1 và chính nó. Các số đó được gọi là số nguyên tố.
Các số 4, 6, 34 có nhiều hơn hai ước. Các số đó được gọi là hợp số.
Luyện tập vận dụng 1 trang 41 Toán 6 tập 1 CD
Cho các số 11, 29, 35, 38. Trong các số đó:
a) Số nào là số nguyên tố? Vì sao?
b) Số nào là hợp số? Vì sao?
Trả lời:
a) Số 11 là số nguyên tố vì nó lớn hơn 1, chỉ có hai ước là 1 và 11.
Số 29 là số nguyên tổ vì nó lớn hơn 1, chỉ có hai ước là 1 và 29.
b) Ta có số 35 có chữ số tận cùng là 5 nên nó chia hết cho 5. Do đó số 35 là hợp số vì ngoài hai ước là 1 và 35, nó còn có ít nhất một ước nữa là 5.
Ta có số 38 có chữ số tận cùng là 8 nên nó chia hết cho 2. Do đó số 38 là hợp số vì ngoài hai ước là 1 và 38, nó còn có ít nhất một ước nữa là 2.
Luyện tập vận dụng 2 trang 42 Toán 6 tập 1 CD
Tìm các ước nguyên tố của: 23, 24, 26, 27.
Trả lời:
Để tìm các ước nguyên tố của một số thì ta tìm các ước của số đó trước, rồi xét xem trong các ước đó, ước nào là số nguyên tố thì số đó được gọi là ước nguyên tố của số đã cho.
– Để tìm các ước của số 23 ta lấy 23 lần lượt chia cho các số tự nhiên từ 1 đến 23. Các phép chia hết là: 23 : 1 = 23; 23 : 23 = 1.
Do đó các ước của số 23 là: 1; 23, trong hai ước này ta thấy số 23 là số nguyên tố (vì nó lớn hơn 1 và chỉ có hai ước là 1 và chính nó)
Vậy ước nguyên tố của số 23 là 23.
(Cách giải khác: Vì 23 là số nguyên tố nên ước nguyên tố của 23 là 23.)
– Để tìm các ước của số 24 ta lấy 24 lần lượt chia cho các số tự nhiên từ 1 đến 24. Các phép chia hết là:
24 : 1 = 24; 24 : 2 = 12; 24 : 3 = 8; 24 : 4 = 6; 24: 6 = 4; 24 : 8 = 3; 24 : 12 = 2; 24 : 24 = 1
Do đó các ước của số 24 là: 1; 2; 3; 4; 6; 8; 12; 24, trong đó chỉ có 2 và 3 là số nguyên tố (vì nó lớn hơn 1 và chỉ có 2 ước là 1 và chính nó)
Vậy các ước nguyên tố của số 24 là: 2 và 3.
– Để tìm các ước của số 26 ta lấy 26 lần lượt chia cho các số tự nhiên từ 1 đến 26. Các phép chia hết là:
26 : 1 = 26; 26 : 2 = 13; 26 : 13 = 2; 26 : 26 = 1
Do đó các ước của số 26 là: 1; 2; 13; 26, trong đó chỉ có số 2 và 13 là số nguyên tố (vì nó lớn hơn 1 và chỉ có 2 ước là 1 và chính nó)
Vậy các ước nguyên tố của 26 là: 2 và 13
– Để tìm các ước của số 27 ta lấy 27 lần lượt chia cho các số tự nhiên từ 1 đến 27. Các phép chia hết là:
27 : 1 = 27; 27 : 3 = 9; 27 : 9 = 3; 27 : 27 = 1
Do đó các ước của số 27 là: 1; 3; 9; 27, trong đó chỉ có số 3 là số nguyên tố (vì nó lớn hơn 1 và chỉ có 2 ước là 1 và chính nó)
Vậy ước nguyên tố của 27 là: 3.
Luyện tập vận dụng 3 trang 42 Toán 6 tập 1 CD
Viết hai số chỉ có ước nguyên tố là 3.
Trả lời:
Theo bài Luyện tập vận dụng 2 trang 42 Toán 6 tập 1 CD, số chỉ có ước nguyên tố là 3 là 27
Ta cũng có thể tìm được các số khác thỏa mãn yêu cầu bài toán, ví dụ như các số: 3; 9; 81; 243;…
Nhận xét: Các số tự nhiên có dạng 3n với n là số tự nhiên khác 0 đều là các số thỏa mãn yêu cầu bài toán.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 trang 42 43 sgk Toán 6 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 42 Toán 6 tập 1 CD
Cho các số 36, 37, 69, 75. Trong các số đó:
a) Số nào là số nguyên tố? Vì sao?
b) Số nào là hợp số? Vì sao?
Bài giải:
a) Số 37 là số nguyên tố vì nó lớn hơn 1, chỉ có hai ước là 1 và 37.
b) Ta có
Số 36 có chữ số tận cùng là 6 nên nó chia hết cho 2. Do đó số 36 là hợp số vì ngoài hai ước là 1 và 36, nó còn có ít nhất một ước nữa là 2.
Số 69 có tổng các chữ số là 6 + 9 = 15 chia hết cho 3 nên số 69 chia hết cho 3. Do đó số 69 là hợp số vì ngoài hai ước là 1 và 69 thì nó còn có ít nhất một ước nữa là 3.
Số 75 có chữ số tận cùng là 5 nên nó chia hết cho 5. Do đó 75 là hợp số vì ngoài hai ước là 1 và 75, nó còn có ít nhất một ước nữa là 5.
Giải bài 2 trang 42 Toán 6 tập 1 CD
Hãy chỉ ra một số nguyên tố lớn hơn 40 và nhỏ hơn 50.
Bài giải:
Các số tự nhiên lớn hơn 40 và nhỏ hơn 50 là: 41; 42; 43; 44; 45; 46; 47; 48; 49.
Trong các số trên, ta thấy có số 41, 43 và 47 là hai số nguyên tố vì nó các số lớn hơn 1 và chỉ có 2 ước là 1 và chính nó.
Do đó đề bài yêu cầu các em chỉ ra một số nguyên tố lớn hơn 40 và nhỏ hơn 50 thì các em chọn 1 trong hai câu trả lời sau:
– Một số nguyên tố lớn hơn 40 và nhỏ hơn 50 là: 41 (vì 41 lớn hơn 1 và chỉ có hai ước là 1 và 41).
– Một số nguyên tố lớn hơn 40 và nhỏ hơn 50 là: 43 (vì 43 lớn hơn 1 và chỉ có hai ước là 1 và 43).
– Một số nguyên tố lớn hơn 40 và nhỏ hơn 50 là: 47 (vì 47 lớn hơn 1 và chỉ có hai ước là 1 và 47).
Giải bài 3 trang 42 Toán 6 tập 1 CD
Mỗi phát biểu sau đúng hay sai? Vì sao?
a) Một số tự nhiên không là số nguyên tố thì sẽ là hợp số.
b) Mọi số nguyên tố đều là số lẻ.
c) 3 là ước nguyên tố của 6 nên 3 cũng là ước nguyên tố của 18.
d) Mọi số tự nhiên đều có ước nguyên tố.
Bài giải:
a) Sai. Vì số 1 và 0 không phải là số nguyên tố cũng không phải là hợp số.
b) Sai. Vì có 2 là số nguyên tố chẵn duy nhất.
c) Đúng. Vì 18 luôn chia hết cho 3.
d) Sai. Vì số 1 chỉ có ước là 1 mà 1 không là số nguyên tố nên 1 không có ước nguyên tố.
Giải bài 4 trang 42 Toán 6 tập 1 CD
Tìm các ước nguyên tố của: 36, 49, 70.
Bài giải:
Để tìm các ước nguyên tố của một số thì ta tìm các ước của số đó trước, rồi xét xem trong các ước đó, ước nào là số nguyên tố thì số đó được gọi là ước nguyên tố của số đã cho.
– Để tìm các ước của số 36, ta lấy 36 lần lượt chia cho các số tự nhiên từ 1 đến 36. Các phép chia hết là:
36 : 1 = 36; 36 : 2 = 18; 36 : 3 = 12; 36 : 4 = 9; 36 : 6 = 6; 36 : 9 = 4; 36 : 12 = 3; 36 : 18 = 2; 36 : 36 = 1
Do đó các ước của số 36 là: 1; 2; 3; 4; 6; 9; 12; 18; 36, trong đó có số 2; 3 là các số nguyên tố.
Vậy các ước nguyên tố của 36 là: 2; 3.
– Để tìm các ước của số 49, ta lấy 49 lần lượt chia cho các số tự nhiên từ 1 đến 49. Các phép chia hết là:
49 : 1= 49; 49 : 7 = 7; 49 : 49 = 1
Do đó các ước của số 49 là: 1; 7; 49, trong đó có số 7 là số nguyên tố.
Vậy ước nguyên tố của 49 là: 7.
– Để tìm các ước của số 70, ta lấy 70 lần lượt chia cho các số tự nhiên từ 1 đến 70.
Ta tìm được các ước của 70 là: 1; 2; 5; 7; 10; 14; 35; 70, trong đó có các số 2; 5; 7 là các số nguyên tố.
Vậy các ước nguyên tố của 70 là: 2; 5; 7.
Giải bài 5 trang 42 Toán 6 tập 1 CD
Hãy viết ba số:
a) Chỉ có ước nguyên tố là 2.
b) Chỉ có ước nguyên tố là 5
Bài giải:
a) Các số chỉ có ước nguyên tố là 2 là các bội của 2 và không nhận ước nguyên tố nào khác ngoài 2.
Do đó ta có 3 số chỉ có ước nguyên tố là 2 là: 2; 4; 8.
(Ta có thể chứng minh được các số thỏa mãn yêu cầu bài toán có dạng 2n, do đó các em có thể đưa ra bộ ba số tùy ý khác thỏa mãn yêu cầu).
b) Các số chỉ có ước nguyên tố là 5 là các bội của 5 và không nhận ước nguyên tố nào khác ngoài 5.
Do đó ta có 3 số chỉ có ước nguyên tố là 5 là: 5; 25; 125.
(Ta có thể chứng minh được các số thỏa mãn yêu cầu bài toán có dạng 5n, do đó các em có thể đưa ra bộ ba số tùy ý khác thỏa mãn yêu cầu).
Giải bài 6 trang 43 Toán 6 tập 1 CD
Bạn An nới với bạn Bình: “Đầu tiên tôi có 11 là số nguyên tố. Cộng 2 vào 11 tôi được 13 là số nguyên tố. Cộng 4 vào 13 tôi được 17 cũng là số nguyên tố. Tiếp theo, cộng 6 vào 17 tôi được 23 cũng là số nguyên tố. Cứ thực hiện như thế, mọi số nhận được đều là số nguyên tố”. Hỏi cách tìm số nguyên tố của bạn An có đúng không?
Bài giải:
Cách tìm số nguyên tố của bạn An là không đúng vì ta thực hiện tiếp như sau:
Cộng 8 vào 23 ta được 31 là số nguyên tố.
Cộng 10 vào 31 ta được 41 là số nguyên tố.
Cộng 12 vào 41 ta được 53 là số nguyên tố.
Cộng 14 vào 53 ta được 67 là số nguyên tố.
Cộng 16 vào 67 ta được 83 là số nguyên tố.
Cộng 18 vào 83 ta được 101 là số nguyên tố.
Cộng 20 vào 101 ta được 121 KHÔNG phải là số nguyên tố vì 121 chia hết cho 11, do đó ngoài 2 ước là 1 và 121 thì số 121 còn có ước khác là 11 nên nó là hợp số.
Vậy cứ tiếp tục thực hiện theo cách của bạn An thì mọi số nhận được không phải tất cả đều là số nguyên tố, nên cách tìm này là sai.
CÓ THỂ EM CHƯA BIẾT
Sàng Ơ-ra-tô-xten (Eratosthenes)
Để tìm số nguyên tố nhỏ hơn 50, ta làm như sau:
• Viết tất cả các số tự nhiên từ 2 đến 50.
• Khoanh tròn số 2, gạch tất cả các số là bội của 2 mà lớn hơn 2:
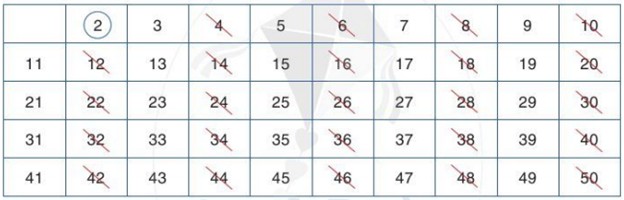
• Khoanh tròn số 3, gạch tất cả các số là bội của 3 mà lớn hơn 3
• Khoanh tròn số 5, gạch tất cả các số là bội của 5 mà lớn hơn 5.
• Khoanh tròn số 7, gạch tất cả các số là bội của 7 mà lớn hơn 7.
• Các số không bị gạch trong bảng đều là số nguyên tố.
Các số nguyên tố nhỏ hơn 50 là: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Số nguyên tố nhỏ nhất là số 2 và đó là số nguyên tố chẵn duy nhất.
Bằng cách tương tự như thế, ta có thể lọc ra tất cả các số nguyên tố nhỏ hơn một số tự nhiên n cho trước. Cách làm đó được gọi là sàng Ơ-ra-tô-xten.
Câu hỏi trang 43 Toán 6 tập 1 CD
Em hãy sử dụng sàng Ơ-ra-tô-xten để tìm tất cả các số nguyên tố nhỏ hơn 100.
Trả lời:
Ta tiếp tục thực hiện với các số từ 51 đến 100 bằng cách:
Viết các số từ 51 đến 100, gạch các số là bội của 2, 3, 5, 7

Ta tìm thêm được các số nguyên tố từ 51 đến 100 là: 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Vậy bằng sàng Ơ-ra-tô-xten ta tìm được các số nguyên tố nhỏ hơn 100 là: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Bài trước:
👉 Giải bài 1 2 3 4 5 trang 39 40 sgk Toán 6 tập 1 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 trang 46 sgk Toán 6 tập 1 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 trang 42 43 sgk Toán 6 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 6 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
