Nội Dung
Hướng dẫn giải Bài §5. Phép chia đa thức một biến sgk Toán 7 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 6 trang 67 sgk Toán 7 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§5. PHÉP CHIA ĐA THỨC MỘT BIẾN
Câu hỏi khởi động trang 64 Toán 7 tập 2 CD
Trong quá trình biến đổi và tính toán những biểu thức đại số, nhiều khi ta phải thực hiện phép chia một đa thức (một biến) cho một đa thức (một biến) khác, chẳng hạn ta cần thực hiện phép chia sau: \(({x^3} + 1):({x^2} – x + 1)\).
Làm thế nào để thực hiện được phép chia một đa thức cho một đa thức khác?
Trả lời:
Để thực hiện phép chia một đa thức cho một đa thức khác, ta làm như sau:
– Bước 1:
+ Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
+ Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
+ Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
– Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.
I. CHIA ĐƠN THỨC CHO ĐƠN THỨC
Hoạt động 1 trang 64 Toán 7 tập 2 CD
Thực hiện phép tính:
a) \({x^5}:{x^3}\);
b) \((4{x^3}):{x^2}\);
c) \((a{x^m}):(b{x^n})\) (a ≠ 0; b ≠ 0; m, n \(\in\) N, m ≥ n).
Trả lời:
a) Ta có:
\({x^5}:{x^3} = {x^{5 – 3}} = {x^2}\).
b) Ta có:
\((4{x^3}):{x^2} = (4:1).({x^3}:{x^2}) = 4x\).
c) Ta có:
\((a{x^m}):(b{x^n}) = (a:b).({x^m}:{x^n}) = (a:b).{x^{m – n}}\) (với a ≠ 0; b ≠ 0; m, n \(\in\) N, m ≥ n).
Luyện tập vận dụng 1 trang 64 Toán 7 tập 2 CD
Tính:
a) \((3{x^6}):(0,5{x^4})\);
b) \(( – 12{x^{m + 2}}):(4{x^{n + 2}})\) (m, n \(\in\) N, m ≥ n).
Trả lời:
a) Ta có:
\((3{x^6}):(0,5{x^4}) = (3:0,5).({x^6}:{x^4}) = 6.{x^{6 – 4}} = 6{x^2}\);
b) Ta có:
\((- 12{x^{m + 2}}):(4{x^{n + 2}}) = ( – 12:4).({x^{m + 2}}:{x^{n + 2}}) \\= – 3.{x^{m + 2 – n – 2}} = – 3.{x^{m – n}}\) ( với m, n \(\in\) N, m ≥ n).
II. CHIA ĐA THỨC CHO ĐƠN THỨC
Hoạt động 2 trang 64 Toán 7 tập 2 CD
Ở Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là \(A = ac,B = bc\). Biết \(MN = c\).
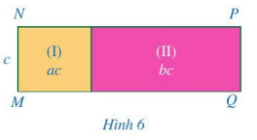
a) Tính NP.
b) So sánh: \((A + B):c\) và \(A:c + B:c\).
Trả lời:
a) Ta có:
Diện tích hình chữ nhật MNPQ bằng diện tích hình chữ nhật (I) + diện tích hình chữ nhật (II)
\( = ac + bc = (a + b).c\)
Mà $MN = c$
Do đó \(NP = (a + b).c:c = a + b\).
b) Ta có:
$(A + B):c = (ac + bc):c = a + b\\A:c + B:c = ac:c + bc:c = a + b$
Vậy \((A + B):c\) =\(A:c + B:c\).
Hoạt động 3 trang 65 Toán 7 tập 2 CD
Cho đa thức \(P(x) = 4{x^2} + 3x\) và đơn thức \(Q(x) = 2x\).
a) Hãy chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x).
b) Hãy cộng các thương vừa tìm được.
Trả lời:
a) Các đơn thức có trong đa thức P(x) là: \(4{x^2};3x\).
Chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x) được kết quả lần lượt là:
\(4{x^2}:2x = (4:2).({x^2}:x) = 2x\).
\(3x:2x = (3:2).(x:x) = \dfrac{3}{2}\).
b) Cộng các thương vừa tìm được \( = 2x + \dfrac{3}{2}\).
Luyện tập vận dụng 2 trang 65 Toán 7 tập 2 CD
Tính:
\((\dfrac{1}{2}{x^4} – \dfrac{1}{4}{x^3} + x):( – \dfrac{1}{8}x)\).
Trả lời:
Ta có:
$(\dfrac{1}{2}{x^4} – \dfrac{1}{4}{x^3} + x):( – \dfrac{1}{8}x) \\= \dfrac{1}{2}{x^4}:( – \dfrac{1}{8}x) – \dfrac{1}{4}{x^3}:( – \dfrac{1}{8}x) + x:( – \dfrac{1}{8}x)\\ = (\dfrac{1}{2}: – \dfrac{1}{8}).({x^4}:x) – (\dfrac{1}{4}: – \dfrac{1}{8}).({x^3}:x) + (1: – \dfrac{1}{8}).(x:x)\\ = – 4.{x^{4 – 1}} – ( – 2).{x^{3 – 1}} + ( – 8).{x^{1 – 1}}\\ = – 4{x^3} + 2{x^2} – 8$.
III. CHIA ĐA THỨC MỘT BIẾN ĐÃ SẮP XẾP
Hoạt động 4 trang 65 Toán 7 tập 2 CD
Thực hiện phép chia:
a) $(2x^2 + 5x + 2) : (2x + 1)$;
b) $(3x^3 – 5x^2 + 2) : (x^2 + 1)$.
Trả lời:
a) • Lấy $2x^2$ chia cho $2x$ được $x$, viết $x$.
Lấy $x$ nhân với $2x + 1$ được $2x^2 + x$, viết $2x^2 + x$.
Lấy $2x^2 + 5x + 2$ trừ đi $2x^2 + x$ được $4x + 2$, viết $4x + 2$.
• Lấy $4x$ chia cho $2x$ được $2$, viết $2$.
Lấy $2$ nhân với $2x + 1$ được $4x + 2$, viết $4x + 2$.
Lấy $4x + 2$ trừ $4x + 2$ được $0$, viết $0$.
Ta có phép tính như sau:
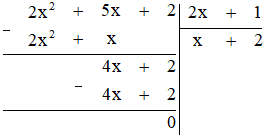
Vậy $(2x^2 + 5x + 2) : (2x + 1) = x + 2$.
b) • Lấy $3x^3$ chia cho $x^2$ được $3x$, viết $3x$.
Lấy $3x$ nhân với $x^2 + 1$ được $3x^3 + 3x$, viết $3x^3 + 3x$.
Lấy $3x^3 – 5x^2 + 2$ trừ đi $3x^3 + 3x$ được $-5x^2 – 3x + 2$, viết $-5x^2 – 3x + 2$.
• Lấy $-5x^2$ chia cho $x^2$ được $-5$, viết $-5$.
Lấy $-5$ nhân với $x^2 + 1$ được $-5x^2 – 5$, viết $-5x^2 – 5$.
Lấy $-5x^2 – 3x + 2$ trừ đi $-5x^2 – 5$ được $-3x + 7$, viết $-3x + 7$.
Bậc của đa thức -$3x + 7$ bằng $1$, nhỏ hơn bậc của đa thức $x^2 + 1$ bằng $2$ nên phép chia kết thúc.
Ta có phép tính như sau:
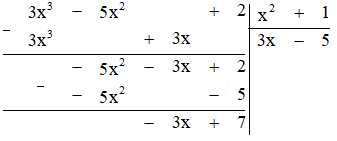
Vậy $(3x^3 – 5x^2 + 2) : (x^2 + 1) = (3x – 5)$ (dư $-3x + 7$).
Nói cách khác, ta có: $3x^3 – 5x^2 + 2 = (3x – 5) . (x^2 + 1) + (-3x + 7)$.
Luyện tập vận dụng 3 trang 66 Toán 7 tập 2 CD
Tính:
a) \(({x^3} + 1):({x^2} – x + 1)\);
b) \((8{x^3} – 6{x^2} + 5):({x^2} + x + 1)\).
Trả lời:
a) Thực hiện phép chia ta được:
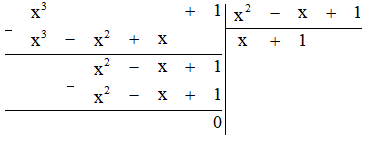
Vậy \(({x^3} + 1):({x^2} – x + 1) = x + 1\).
b) Thực hiện phép chia ta được:
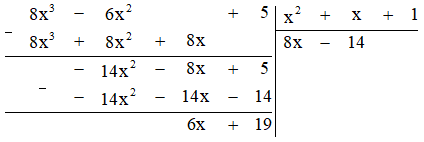
Vậy \((8{x^3} – 6{x^2} + 5) : ({x^2} + x + 1) = (8x – 14)\) (dư $6x + 19$).
Nói cách khác, ta có: \((8{x^3} – 6{x^2} + 5) = ({x^2} + x + 1)(8x – 14) + (6x + 19)\)
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 trang 67 sgk Toán 7 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 67 Toán 7 tập 2 CD
Tính:
a) \((4{x^3}):( – 2{x^2})\);
b) \(( – 7{x^2}):(6x)\);
c) \(( – 14{x^4}):( – 8{x^3})\).
Bài giải:
a) Ta có:
\((4{x^3}):( – 2{x^2}) = [4: (- 2)].({x^3}:{x^2})\\ = – 2.{x^{3 – 2}} = – 2x\)
b) Ta có:
\(( – 7{x^2}):(6x) = ( – 7:6).({x^2}:x)\\= – \dfrac{7}{6}.{x^{2 – 1}} = – \dfrac{7}{6}.x\)
c) Ta có:
\(( – 14{x^4}):( – 8{x^3}) = ( – 14: – 8).({x^4}:{x^3})\\= \dfrac{7}{4}.{x^{4 – 3}} = \dfrac{7}{4}.x\).
Giải bài 2 trang 67 Toán 7 tập 2 CD
Tính:
a) \((8{x^3} + 2{x^2} – 6x):(4x)\);
b) \((5{x^3} – 4x):( – 2x)\);
c) \(( – 15{x^6} – 24{x^3}):( – 3{x^2})\).
Bài giải:
a) Ta có:
$(8{x^3} + 2{x^2} – 6x):(4x)\\= 8{x^3}:(4x) + 2{x^2}:(4x) – (6x):(4x) \\= (8:4).({x^3}:x) + (2:4).({x^2}:x) – (6:4).(x:x)\\= 2{x^2} + \dfrac{1}{2}x – \dfrac{3}{2}$
b) Ta có:
$(5{x^3} – 4x):( – 2x)\\= 5{x^3}:( – 2x) – 4x:( – 2x)\\= (5: – 2).({x^3}:x) – (4: – 2).(x:x)\\= – \dfrac{5}{2}{x^{3 – 1}} – ( – 2)\\= – \dfrac{5}{2}{x^2} + 2$
c) Ta có:
$(- 15{x^6} – 24{x^3}):( – 3{x^2})\\= ( – 15{x^6}):( – 3{x^2}) + ( – 24{x^3}):( – 3{x^2})\\ = (- 15: – 3).({x^6}:{x^2}) + ( – 24: – 3).({x^3}:{x^2})\\ = 5.{x^{6 – 2}} + 8.{x^{3 – 2}}\\= 5{x^4} + 8x$.
Giải bài 3 trang 67 Toán 7 tập 2 CD
Tính:
a) \(({x^2} – 2x + 1):(x – 1)\);
b) \(({x^3} + 2{x^2} + x):({x^2} + x)\);
c) \(( – 16{x^4} + 1):( – 4{x^2} + 1)\);
d) \(( – 32{x^5} + 1):( – 2x + 1)\).
Bài giải:
a) Thực hiện phép tính ta được:
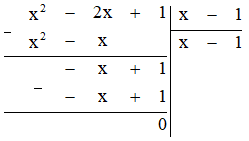
Vậy $(x^2 – 2x + 1) : (x – 1) = x – 1$.
b) Thực hiện phép tính ta được:

Vậy $(x^3 + 2x^2 + x) : (x^2 + x) = x + 1$.
c) Thực hiện phép tính ta được:
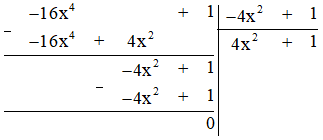
Vậy $(-16x^4 + 1) : (-4x^2 + 1) = 4x^2 + 1$.
d) Thực hiện phép tính ta được:

Vậy \(( – 32{x^5} + 1):( – 2x + 1) = 16{x^4} + 8{x^3} + 4{x^2} + 2x + 1\).
Giải bài 4 trang 67 Toán 7 tập 2 CD
Tính:
a) \((6{x^2} – 2x + 1):(3x – 1)\);
b) \((27{x^3} + {x^2} – x + 1):( – 2x + 1)\);
c) \((8{x^3} + 2{x^2} + x):(2{x^3} + x + 1)\);
d) \((3{x^4} + 8{x^3} – 2{x^2} + x + 1):(3x + 1)\).
Bài giải:
a) Thực hiện phép tính ta được:
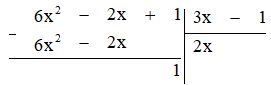
Vậy $(6x^2 – 2x + 1) : (3x – 1) = 2x$ (dư 1).
Hay: $6x^2 – 2x + 1 = 2x . (3x – 1) + 1$.
b) Thực hiện phép tính ta được:
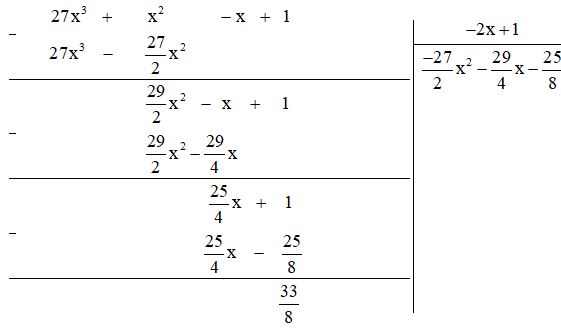
Vậy \((27x^3 + x^2 – x + 1):( – 2x + 1) = \frac{- 27}{2}x^2 – \frac{29}{4}x – \frac{25}{8}\) (dư $\frac{33}{8}$).
Hay: $(27x^3 + x^2 – x + 1) = (\frac{- 27}{2}x^2 – \frac{29}{4}x – \frac{25}{8})(- 2x + 1) + \frac{33}{8}$.
c) Thực hiện phép tính ta được:
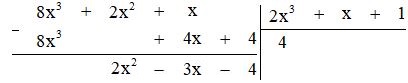
Vậy \((8{x^3} + 2{x^2} + x):(2{x^3} + x + 1) = 4\) (dư $(x^2 – 3x – 4$.
Hay $8x^3 + 2x^2 + x = 4(2x^3 + x + 1) + (2x^2 – 3x – 4)$.
d) Thực hiện phép tính ta được:
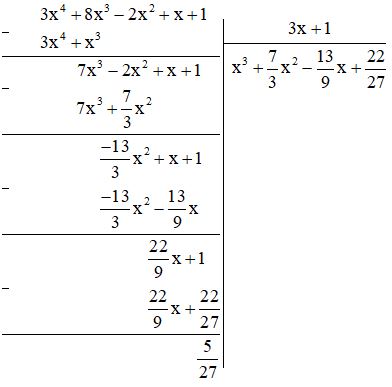
Vậy \((3{x^4} + 8{x^3} – 2{x^2} + x + 1):(3x + 1) = (x^3 + \frac{7}{3}x^2 – \frac{13}{9}x + \frac{22}{27}\) (dư $ \frac{5}{27}$).
Hay \((3{x^4} + 8{x^3} – 2{x^2} + x + 1) = (3x + 1)(x^3 + \frac{7}{3}x^2 – \frac{13}{9}x + \frac{22}{27}) + \frac{5}{27}\).
Giải bài 5 trang 67 Toán 7 tập 2 CD
Một công ty sau khi tăng giá 30 nghìn đồng mỗi sản phẩm so với giá ban đầu là 2x (nghìn đồng) thì có doanh thu là \(6{x^2} + 170x + 1200\) (nghìn đồng). Tính số sản phẩm mà công ty đó đã bán được theo x.
Bài giải:
Giá tiền mỗi sản phẩm sau khi tăng giá là \(2x + 30\) (nghìn đồng).
Sau khi tăng giá thì công ty có doanh thu là \(6{x^2} + 170x + 1200\) (nghìn đồng).
Thực hiện phép tính ta được:
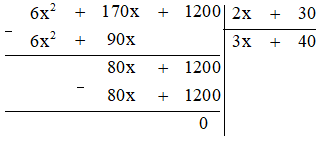
Vậy số sản phẩm mà công ty đó đã bán được theo x là \(3x + 40\) (sản phẩm).
Giải bài 6 trang 67 Toán 7 tập 2 CD
Một hình hộp chữ nhật có thể tích là \({x^3} + 6{x^2} + 11x + 6\) \((c{m^3})\). Biết đáy là hình chữ nhật có các kích thước là \(x + 1\)(cm) và \(x + 2\)(cm). Tính chiều cao của hình hộp chữ nhật đó theo x.
Bài giải:
Diện tích mặt đáy của hình hộp chữ nhật là:
\((x + 1).(x + 2) = x(x + 2) + 1.(x + 2)\\ = {x^2} + 2x + x + 2 = {x^2} + 3x + 2\) \((c{m^2})\).
Chiều cao của hình hộp chữ nhật là thương trong phép chia thể tích hình hộp chữ nhật cho diện tích đáy của hình hộp chữ nhật đó.
Thực hiện phép tính ta được:
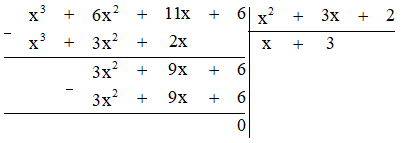
Vậy chiều cao của hình hộp chữ nhật đó theo x là \(x + 3\) (cm).
Bài trước:
👉 Giải bài 1 2 3 4 5 trang 63 sgk Toán 7 tập 2 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 68 69 sgk Toán 7 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 trang 67 sgk Toán 7 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
