Nội Dung
Hướng dẫn giải Bài §12. Tính chất ba đường trung trực của tam giác sgk Toán 7 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 trang 115 sgk Toán 7 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§12. TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC
Câu hỏi khởi động trang 112 Toán 7 tập 2 CD
Hình 121 minh họa biển giới thiệu quần thể di tích, danh thắng cấp Quốc gia núi Dũng Quyết và khu vực Phượng Hoàng Trung Đô ở tỉnh Nghệ An (Hình 120).

Làm thế nào để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121?
Trả lời:
Để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121, ta xác định ba đường trung trực của tam giác được tạo thành từ ba đỉnh đó rồi xác định giao điểm của đường trung trực đó.
I. ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC
Hoạt động 1 trang 112 Toán 7 tập 2 CD
Cho tam giác ABC như Hình 122. Vẽ đường trung trực d của đoạn thẳng BC.
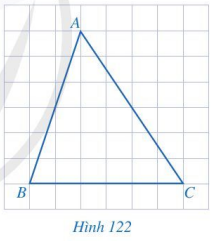
Trả lời:
Lấy M là trung điểm của đoạn thẳng BC. Đường thẳng d là đường thẳng đi qua M và vuông góc với BC.
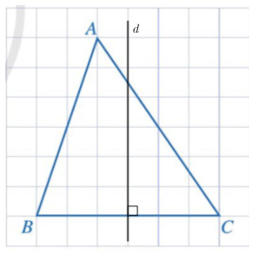
Luyện tập vận dụng 1 trang 113 Toán 7 tập 2 CD
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.
Trả lời:
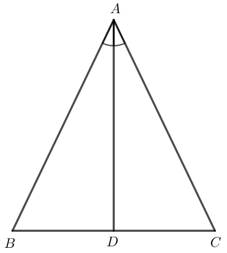
AD là phân giác của góc A nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác ABD và tam giác ACD có:
$AB = AC$ (tam giác ABC cân tại A)
\(\widehat {BAD} = \widehat {CAD}\)
$AD$ chung
Vậy \(\Delta ABD = \Delta ACD\) (c.g.c)
⇒ \(BD = CD\) (2 cạnh tương ứng).
⇒ D là trung điểm của cạnh BC.
Vì \(\Delta ABD = \Delta ACD\) nên \(\widehat {ADB} = \widehat {ADC}\) (2 góc tương ứng).
Mà \(\widehat {ADB} + \widehat {ADC}=180^0\) (2 góc kề bù) nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ ⇒ AD \bot BC\).
Vậy AD là đường trung trực của tam giác ABC.
II. TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC
Hoạt động 2 trang 113 Toán 7 tập 2 CD
Quan sát các đường trung trực của tam giác ABC (Hình 126), cho biết ba đường trung trực đó có cùng đi qua một điểm hay không.
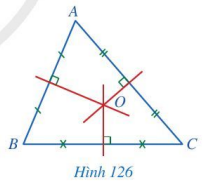
Trả lời:
Ba đường trung trực của tam giác ABC có cùng đi qua một điểm là điểm O.
Luyện tập vận dụng 2 trang 114 Toán 7 tập 2 CD
Trong Hình 127, điểm O có phải là giao điểm của ba đường trung trực của tam giác ABC không?
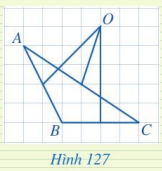
Trả lời:
Điểm O có là giao điểm của ba đường trung trực của tam giác ABC.
Hoạt động 3 trang 114 Toán 7 tập 2 CD
Quan sát giao điểm O của ba đường trung trực của tam giác ABC (Hình 128) và so sánh độ dài ba đoạn thẳng OA, OB, OC.
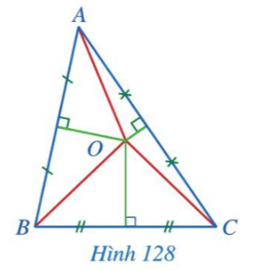
Trả lời:
Do O nằm trên đường trung trực của đoạn thẳng AB nên $OA = OB$.
Do O nằm trên đường trung trực của đoạn thẳng BC nên $OB = OC$.
Do đó $OA = OB = OC$.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 trang 115 sgk Toán 7 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 115 Toán 7 tập 2 CD
Cho tam giác ABC và điểm O thỏa mãn OA = OB = OC. Chứng minh rằng O là giao điểm của ba đường trung trực của tam giác ABC.
Bài giải:
Ta có:
OA = OB nên O nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng). (1)
OB = OC nên O nằm trên đường trung trực của đoạn thẳng BC (tính chất đường trung trực của đoạn thẳng). (2)
OC = OA nên O nằm trên đường trung trực của đoạn thẳng AC (tính chất đường trung trực của đoạn thẳng). (3)
Từ (1), (2), và (3) suy ra O là giao điểm của ba đường trung trực của tam giác ABC.
Giải bài 2 trang 115 Toán 7 tập 2 CD
Cho tam giác ABC. Vẽ điểm O cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:
a) Tam giác ABC nhọn;
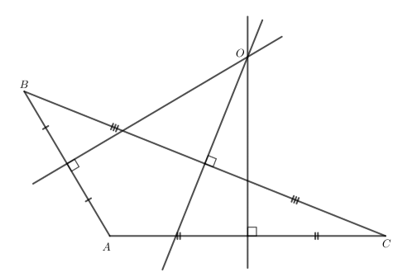
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
Bài giải:
a) Tam giác ABC nhọn, ta có hình vẽ sau:
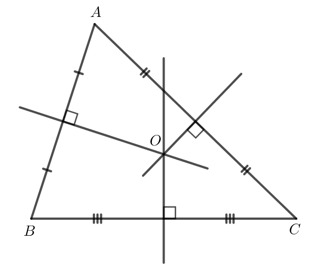
b) Tam giác ABC vuông tại A, ta có hình vẽ sau:
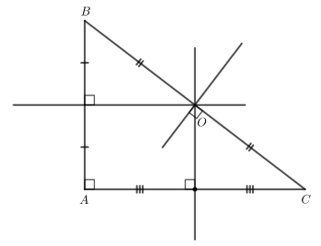
c) Tam giác ABC có góc A tù, ta có hình vẽ sau:
Giải bài 3 trang 115 Toán 7 tập 2 CD
Tam giác ABC có ba đường trung tuyến cắt nhau tại G. Biết rằng điểm G cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều.
Bài giải:
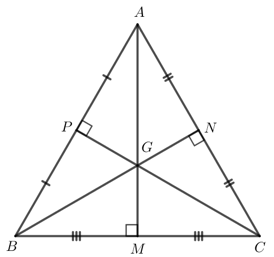
Gọi M, N, P lần lượt là các trung điểm của các đoạn thẳng BC, AC, AB.
Ta có: G là giao điểm của ba đường trung tuyến trong tam giác ABC.
Mà G cũng là giao điểm của ba đường trung trực trong tam giác ABC nên AM, BN, CP là các đường trung trực của tam giác ABC hay \(AM \bot BC; BN \bot AC; CP \bot AB\).
Xét tam giác ABM và tam giác ACM có:
$AM$ chung
\(\widehat {AMB} = \widehat {AMC} (= 90^\circ \)) (vì \(AM \bot BC\))
$BM = MC$ (M là trung điểm của BC)
Vậy \(\Delta ABM = \Delta ACM\) (c.g.c)
⇒ $AB = AC$ (2 cạnh tương ứng). (1)
Tương tự ta có:
\(\Delta BNA = \Delta BNC\) (c.g.c)
⇒ $AB = BC$ (2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: $AB = BC = AC$.
Vậy tam giác ABC đều.
Giải bài 4 trang 115 Toán 7 tập 2 CD
Tam giác ABC có ba đường phân giác cắt nhau tại I. Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC. Chứng minh tam giác ABC đều.
Bài giải:
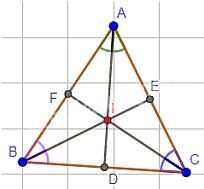
Ta có:
I là giao điểm của ba đường phân giác của tam giác ABC. Đồng thời là giao điểm của ba đường trung trực tam giác ABC nên: \(ID \bot BC; IE \bot AC; IF \bot AB\).
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\) (AD là phân giác của góc A)
$AD$ chung
\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(ID \bot BC\))
Vậy \(\Delta ADB = \Delta ADC\) (g.c.g)
⇒ $AB = AC$ (2 cạnh tương ứng). (1)
Tương tự ta có:
\(\Delta BEA = \Delta BEC\) (g.c.g)
⇒ $BA = BC$ (2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: $AB = BC = AC$.
Vậy tam giác ABC đều.
Giải bài 5 trang 115 Toán 7 tập 2 CD
Cho tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại điểm O nằm trong tam giác. M là trung điểm của BC. Chứng minh:
a) \(OM \bot BC\);
b) \(\widehat {MOB} = \widehat {MOC}\).
Bài giải:
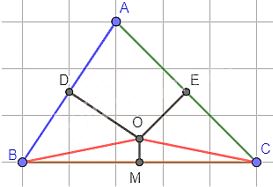
a) Ta có:
Đường trung trực của hai cạnh AB và AC cắt nhau tại O và O nằm trong tam giác. Nên O là giao điểm của ba đường trung trực của tam giác ABC.
Mà M là trung điểm của cạnh BC nên OM là đường trung trực của đoạn thẳng BC hay \(OM \bot BC\).
b) Ta có:
Giao của ba đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.
Hay OB = OC nên tam giác OBC cân tại O.
⇒ \(\widehat {OBC} = \widehat {OCB}\) hay \(\widehat {OBM} = \widehat {OCM}\). (tính chất tam giác cân)
Xét tam giác OMB và tam giác OMC có:
$OB = OC$
\(\widehat {OBM} = \widehat {OCM}\)
$MB = MC$ (M là trung điểm của đoạn thẳng BC)
Vậy \(\Delta OMB = \Delta OMC\) (c.g.c)
⇒ \(\widehat {MOB} = \widehat {MOC}\) (2 góc tương ứng).
Bài trước:
👉 Giải bài 1 2 3 trang 111 sgk Toán 7 tập 2 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 trang 118 sgk Toán 7 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 trang 115 sgk Toán 7 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
