Nội Dung
Hướng dẫn giải Bài 8. Góc ở vị trí đặc biệt. Tia phân giác của một góc sgk Toán 7 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 1 2 3 4 5 trang 45 sgk Toán 7 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
BÀI 8. GÓC Ở VỊ TRÍ ĐẶC BIỆT. TIA PHÂN GIÁC CỦA MỘT GÓC
Bài toán mở đầu trang 40 Toán 7 tập 1 KNTT
Khi đặt các dây lạt để cắt bánh chưng, các dây lạt tạo ra trên mặt bánh chưng những cặp góc đặc biệt. Những cặp góc đó có mối quan hệ với nhau như thế nào, chúng ta cùng tìm hiểu trong bài học này!

Trả lời:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Khi đặt các dây lạt để cắt bánh chưng, các dây lạt tạo ra trên mặt bánh chưng những cặp góc kề bù, đối đỉnh, các cặp góc bằng nhau được tạo bởi tia phân giác của góc.
1. GÓC Ở VỊ TRÍ ĐẶC BIỆT
Hoạt động 1 trang 41 Toán 7 tập 1 KNTT
Quan sát hình vẽ bên. Em hãy nhận xét về mối quan hệ về đỉnh, về cạnh của hai góc được đánh dấu.
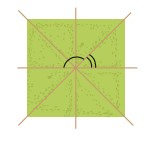
Trả lời:
Hai góc được đánh dấu trên hình có chung một đỉnh và chung một cạnh, hai cạnh còn lại là hai tia đối nhau.
Hoạt động 2 trang 41 Toán 7 tập 1 KNTT
Cho ba tia Ox, Oy, Oz như Hình 3.1, trong đó Ox và Oy là hai tia đối nhau.
a) Em hãy nhận xét về quan hệ về đỉnh, về cạnh của hai góc xOz và zOy.
b) Đo rồi tính tổng số đo góc hai góc xOz và zOy.
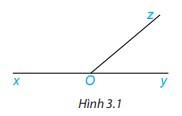
Trả lời:
a) Đỉnh của góc xOz và zOy cùng là đỉnh O.
2 góc xOz và zOy có chung cạnh Oz, cạnh còn lại (Ox và Oy) là 2 tia đối nhau.
b) Dùng thước đo góc ta đo được:
\(\widehat{xOz}=40^0, \widehat{zOy}=140^0\)
Tổng số đo hai góc zOy và xOz là:
\(\widehat{xOz}+\widehat{zOy}=40^0+140^0=180^0\)
Câu hỏi trang 41 Toán 7 tập 1 KNTT
Hai góc được đánh dấu trong hình nào dưới đây là hai góc kề bù?
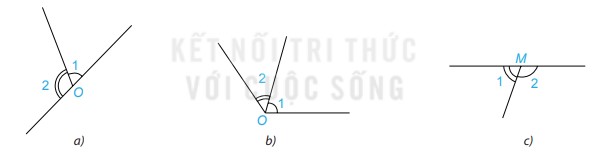
Trả lời:
Xét hình a): \(\widehat {{O_1}} = \widehat {{O_2}}\) là hai góc kề bù vì 2 góc này có một cạnh chung, hai cạnh còn lại là hai tia đối nhau.
Xét hình b): \(\widehat {{O_1}} = \widehat {{O_2}}\) không là hai góc kề bù vì 2 góc này có một cạnh chung nhưng hai cạnh còn lại không là hai tia đối nhau.
Xét hình c): \(\widehat {{M_1}} = \widehat {{M_2}}\) là hai góc kề bù vì 2 góc này có một cạnh chung, hai cạnh còn lại là hai tia đối nhau.
Luyện tập 1 trang 42 Toán 7 tập 1 KNTT
Viết tên hai góc kề bù trong Hình 3.4 và tính số đo góc mOt.
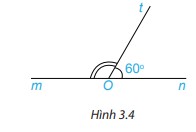
Trả lời:
Hai góc kề bù trong Hình 3.4 là góc mOt và góc nOt.
Do góc mOt và góc nOt là hai góc kề bù nên tổng số đo hai góc mOt và góc nOt bằng 180o.
Khi đó số đo góc mOt bằng:
$\widehat {mOt} = 180^\circ – \widehat {tOn} = 180^\circ – 60^\circ = 120^\circ $.
Vậy số đo góc mOt bằng 120o.
Hoạt động 3 trang 42 Toán 7 tập 1 KNTT
Quan sát hình ảnh hai góc được đánh dấu trong hình bên. Em hãy nhận xét quan hệ về đỉnh, về cạnh của hia góc được đánh dấu.
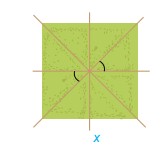
Trả lời:
Hai góc được đánh dấu trên hình có chung đỉnh, mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Hoạt động 4 trang 42 Toán 7 tập 1 KNTT
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O (H.3.5).
a) Dự đoán xem hai góc xOy và x’Oy’ có bằng nhau không?
b) Đo rồi so sánh số đo hai góc xOy và x’Oy’.
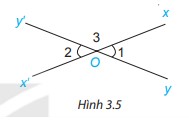
Trả lời:
a) Em dự đoán xem hai góc xOy và x’Oy’ có bằng nhau.
b) Đo rồi so sánh số đo hai góc ta thấy:
\(\widehat{xOy} = \widehat{x’Oy’} = 31^0\)
Câu hỏi trang 42 Toán 7 tập 1 KNTT
Hai góc được đánh dấu trong hình nào dưới đây là hai góc đối đỉnh?
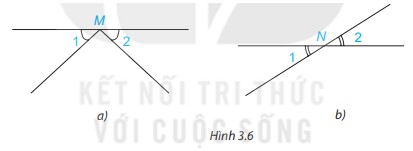
Trả lời:
Hai góc M1 và M2 trong hình a) không phải là hai góc đối đỉnh do có một cạnh của góc M1 không phải tia đối của một cạnh của góc M2.
Hai góc N1 và N2 trong hình b) là hai góc đối đỉnh do mỗi cạnh của góc N1 là tia đối của một cạnh của góc N2.
Vậy 2 góc ở Hình 3.6.b là hai góc đối đỉnh vì 2 góc này có mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Luyện tập 2 trang 43 Toán 7 tập 1 KNTT
Hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho góc xOy vuông (H.3.8). Khi đó các góc yOx’, x’Oy’, xOy’ cũng đều là góc vuông. Vì sao?
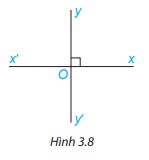
Trả lời:
Góc x’Oy’ và xOy là hai góc đối đỉnh nên \(\widehat {x’Oy’} = \widehat {xOy} = 90^\circ \)
Góc xOy’ và xOy là hai góc kề bù nên
$\widehat {xOy’} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {xOy’} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {xOy’} = 180^\circ – 90^\circ = 90^\circ $
Góc x’Oy và xOy là hai góc kề bù nên
$\widehat {x’Oy} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {x’Oy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {x’Oy} = 180^\circ – 90^\circ = 90^\circ $
Do đó các góc đều là góc vuông.
2. TIA PHÂN GIÁC CỦA MỘT GÓC
Hoạt động 5 trang 43 Toán 7 tập 1 KNTT
Cắt rời một góc xOy từ một tờ giấy rồi gấp sao cho hai cạnh của góc trùng nhau (H.3.9).
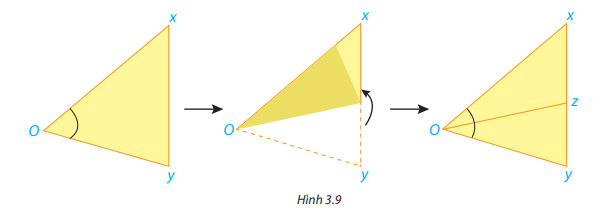
Mở mảnh giấy ra, nếp gấp cho ta hình ảnh tia Oz chia góc ban đầu thành hai góc.
a) Em hãy nhận xét về vị trí của tia Oz so với hai cạnh của góc xOy.
b) Em hãy so sánh hai góc xOz và zOy.
Trả lời:
a) Tia Oz nằm giữa hai cạnh của góc xOy.
b) Hai góc xOz và zOy bằng nhau.
\(\widehat {xOz} = \widehat {zOy}\)
Luyện tập 3 trang 44 Toán 7 tập 1 KNTT
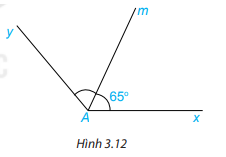
Cho góc xAm có số đo bằng \(65^\circ \) và Am là tia phân giác của góc xAy (H.3.12). Tính số đo góc xAy.
Trả lời:
Ta có Am là tia phân giác của góc xAy nên
$\widehat {xAm} = \frac{1}{2}.\widehat {xAy}\\ \Rightarrow \widehat {xAy} = 2.\widehat {xAm} = 2.65^\circ = 130^\circ $
Vậy số đo góc $\widehat {xAy} = 130^\circ $.
Thực hành trang 44 Toán 7 tập 1 KNTT
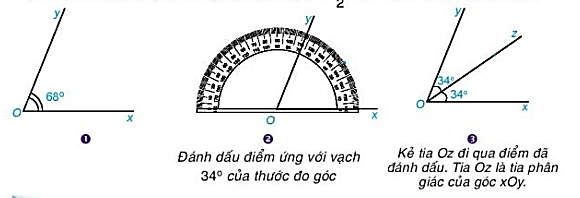
Vẽ tia phân giác Oz của xOy có số đo bằng 68\(^\circ \), sử dụng thước đo góc theo hướng dẫn. Nếu Oz là toa phân giác của góc xOy thì \(\widehat {xOz} = \frac{1}{2}.68^\circ = 34^\circ \). Ta có cách vẽ sau:
Vận dụng trang 45 Toán 7 tập 1 KNTT
Quan sát hình vẽ bên.
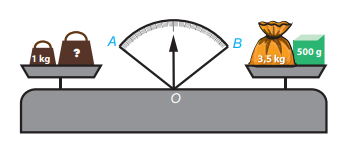
Quả cân ở đĩa cân bên trái nặng bao nhiêu kilogam để cân thăng bằng, tức là kim trên mặt đồng hồ của cân là tia phân giác của góc AOB?
Trả lời:
Đổi 500 g = 0,5 kg.
Khi đó đĩa cân bên phải nặng $3,5 + 0,5 = 4$ kg.
Để cân thăng bằng, tức kim trên mặt đồng hồ của cân là tia phân giác của góc AOB thì quả cân ở đĩa cân bên trái nặng: $4 – 1 = 3$ kg.
Vậy quả cân nặng $3$ kg.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 trang 45 sgk Toán 7 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 3.1 trang 45 Toán 7 tập 1 KNTT
Cho Hình 3.13, hãy kể tên các cặp góc kề bù.
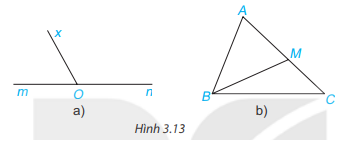
Bài giải:
a) Góc xOm và xOn là 2 góc kề bù vì 2 góc này có chung cạnh Ox, cạnh Om là tia đối của On.
b) Góc AMB và CMB là 2 góc kề bù vì 2 góc này có chung cạnh MB, cạnh MA là tia đối của MC.
Giải bài 3.2 trang 45 Toán 7 tập 1 KNTT
Cho Hình 3.14, hãy kể tên các cặp góc đối đỉnh.
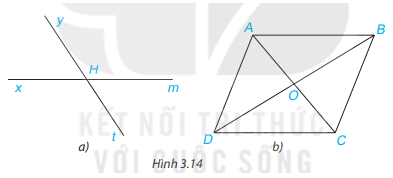
Bài giải:
a) 2 góc xHy và mHt là 2 góc đối đỉnh vì Hx và Hm là 2 tia đối nhau; Hy và Ht là 2 tia đối nhau.
2 góc xHt và mHy là 2 góc đối đỉnh vì Hx và Hm là 2 tia đối nhau; Ht và Hy là 2 tia đối nhau.
b) 2 góc AOB và COD là là 2 góc đối đỉnh vì OA và OC là 2 tia đối nhau; OB và OD là 2 tia đối nhau.
2 góc AOD và COB là là 2 góc đối đỉnh vì OA và OC là 2 tia đối nhau; OD và OB là 2 tia đối nhau.
Giải bài 3.3 trang 45 Toán 7 tập 1 KNTT
Vẽ góc xOy có số đo bằng 60 \(^\circ \). Vẽ tia Om là tia đối của tia Ox.
a) Gọi tên hai góc kề bù có trong hình vừa vẽ.
b) Tính số đo góc yOm.
c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.
Bài giải:
Ta vẽ như sau:
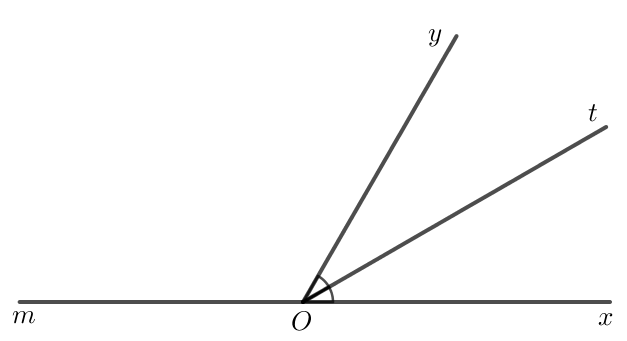
a) Hai góc kề bù có trên hình vừa vẽ là góc xOy và mOy.
b) Vì \(\widehat {xOy} + \widehat {yOm} = 180^\circ \) (2 góc kề bù)
$\Rightarrow 60^\circ + \widehat {yOm} = 180^\circ \\ \Rightarrow \widehat {yOm} = 180^\circ – 60^\circ = 120^\circ $
c) Vì tia Ot là tia phân giác của góc xOy nên
\(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Mà \(\widehat {xOt}\) và \(\widehat {tOm}\) là hai góc kề bù nên
$\widehat {xOt} + \widehat {tOm} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {tOm} = 180^\circ \\ \Rightarrow \widehat {tOm} = 180^\circ – 30^\circ = 150^\circ $
Vậy \(\widehat {tOy} = 30^\circ ;\widehat {tOm} = 150^\circ \)
Giải bài 3.4 trang 45 Toán 7 tập 1 KNTT
Cho Hình 3.15a, biết \(\widehat {DMA} = 45^\circ \). Tính số đo góc DMB.
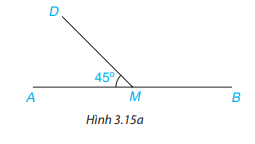
Bài giải:
Vì góc AMD và BMD là hai góc kề bù nên
$\widehat {AMD} + \widehat {BMD} = 180^\circ \\ \Rightarrow 45^\circ + \widehat {BMD} = 180^\circ \\ \Rightarrow \widehat {BMD} = 180^\circ – 45^\circ = 135^\circ $
Vậy \(\widehat {DMB} = 135^\circ \)
Giải bài 3.5 trang 45 Toán 7 tập 1 KNTT
Cho Hình 3.15b, biết \(\widehat {xBm} = 36^\circ \). Tính số đo các góc còn lại trong hình vừa vẽ.
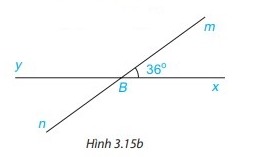
Bài giải:
Vì \(\widehat{xBm}\) và \(\widehat{yBn}\) là hai góc đối đỉnh nên \(\widehat {xBm} = \widehat {yBn}\)
Mà \(\widehat {xBm} = 36^\circ \) nên \(\widehat {yBn} = 36^\circ \)
Vì \(\widehat{xBm}\) và \(\widehat{mBy}\) là hai góc kề bù nên
$\widehat {xBm} + \widehat {mBy} = 180^\circ \\ \Rightarrow 36^\circ + \widehat {mBy} = 180^\circ \\ \Rightarrow \widehat {mBy} = 180^\circ – 36^\circ = 144^\circ $
Vì \(\widehat{mBy}\) và \(\widehat{nBx}\) là hai góc đối đỉnh nên \(\widehat {mBy} = \widehat {nBx}\)
Mà \(\widehat {mBy} = 144^\circ \) nên \(\widehat {nBx} = 144^\circ \)
Bài trước:
👉 Giải bài 27 28 29 30 31 trang 39 sgk Toán 7 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 6 7 8 9 10 11 trang 49 sgk Toán 7 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 trang 45 sgk Toán 7 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
