Nội Dung
Hướng dẫn giải Bài §3. Đường trung bình của tam giác sgk Toán 8 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 trang 65 sgk Toán 8 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
§3. ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
Câu hỏi khởi động trang 62 Toán 8 tập 2 CD
Hình 28 gợi nên hình ảnh tam giác $ABC$ và đoạn thẳng $MN$ với $M, N$ lần lượt là trung điểm của hai cạnh $AB, AC$.

Hai đoạn thẳng $MN$ và $BC$ có mối liên hệ gì?
Trả lời:
Xét tam giác $ABC$ có $M, N$ lần lượt là trung điểm của hai cạnh $AB, AC$ nên $MN$ là đường trung bình của tam giác $ABC$.
Do đó $MN // BC$ và $MN = \frac{1}{2}BC$.
I. ĐỊNH NGHĨA
Hoạt động 1 trang 62 Toán 8 tập 2 CD
Quan sát tam giác $ABC$ ở Hình 29 và cho biết hai đầu mút $D, E$ của đoạn thẳng $DE$ có đặc điểm gì.
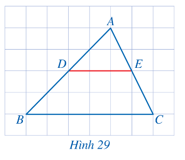
Trả lời:
Quan sát hình ta thấy $D$ và trung điểm của đoạn thẳng $AB$ và $E$ là trung điểm của đoạn thẳng $AC$.
Luyện tập vận dụng 1 trang 62 Toán 8 tập 2 CD
Vẽ tam giác $ABC$ và các đường trung bình của tam giác đó.
Trả lời:
Ta có hình vẽ minh họa sau:
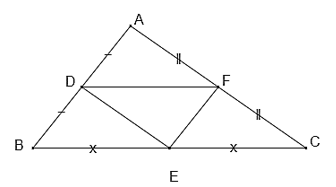
– Vẽ tam giác $ABC$.
– Lấy ba điểm $D, E, F$ lần lượt là trung điểm của các cạnh $AB, BC, CA$.
– Nối $DF, FE, ED$ ta được ba đường trung bình của tam giác $ABC$.
II. TÍNH CHẤT
Hoạt động 2 trang 63 Toán 8 tập 2 CD
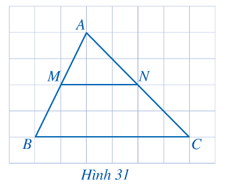
Cho tam giác $ABC$ có $MN$ là đường trung bình (Hình 31).
a) $MN$ có song song với $BC$ hay không? Vì sao?
b) Tỉ số \(\frac{{MN}}{{BC}}\) bằng bao nhiêu?
Trả lời:
a) Vì $MN$ là đường trung bình của tam giác $ABC$ nên $M$ là trung điểm $AB$ và $N$ là trung điểm $AC$.
Khi đó \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) suy ra \(MN\parallel BC\) (Định lý Thales đảo trong tam giác $ABC$).
b) $M$ là trung điểm $AB$ nên \(\frac{{AM}}{{AB}} = \frac{1}{2}\).
Xét tam giác $ABC$ với \(MN\parallel BC\) ta có:
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{1}{2}\) (Hệ quả của định lý Thales).
Luyện tập vận dụng 2 trang 64 Toán 8 tập 2 CD
Cho hình thang $ABCD$ \(\left( {AB\parallel CD} \right)\). Giả sử $M, N, P$ lần lượt là trung điểm của các đoạn thẳng $AD, BC, AC$. Chứng minh:
a) $M, N, P$ thẳng hàng;
b) \(MN = \frac{1}{2}\left( {AB + CD} \right)\).
Trả lời:
Ta có hình vẽ minh họa sau:
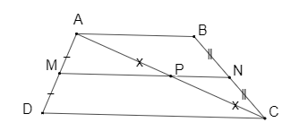
a) Vì $M$ và $P$ lần lượt là trung điểm của hai cạnh $AD, AC$ nên $MP$ là đường trung bình của tam giác $ADC$.
\(\Rightarrow MP\parallel AB\parallel CD\,\,\left( 1 \right)\)
Vì $P$ và $N$ lần lượt là trung điểm của hai cạnh $AC, BC$ nên $PN$ là đường trung bình của tam giác $ABC$.
\(\Rightarrow PN\parallel AB\parallel CD\,\,\left( 2 \right)\)
Từ (1) và (2) ta có \(MP \equiv PN\) hay ba điểm $M, N, P$ thẳng hàng.
b) Vì $MP$ là đường trung bình của tam giác $ADC$ nên \(MP = \frac{1}{2}DC\).
Vì $PN$ là đường trung bình của tam giác $ABC$ nên \(PN = \frac{1}{2}AB\).
Ta có:
\(MN = MP + PN = \frac{1}{2}DC + \frac{1}{2}AB = \frac{1}{2}\left( {DC + AB} \right)\)
Vậy \(MN = \frac{1}{2}\left( {AB + CD} \right)\).
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 trang 65 sgk Toán 8 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 66 Toán 8 tập 2 CD
Cho tam giác $ABC$ có $M$ là trung điểm của $AB$, điểm $N$ thuộc cạnh $AC$ thỏa mãn \(MN//BC\). Chứng minh \(NA = NC\) và \(MN = \frac{1}{2}BC\).
Bài giải:
Ta có hình vẽ minh họa sau:
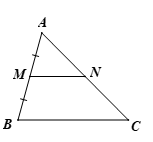
Theo đề bài ta có \(MN//BC\) nên \(\frac{AM}{MB} = \frac{AN}{NC}\)
Mà \( AM = MB\)
\(\Rightarrow \frac{AM}{MB} = \frac{AN}{NC} = 1 \Rightarrow AN = NC\)
⇒ $N$ là trung điểm của $AC$
Khi đó $MN$ là đường trung bình của tam giác $ABC$
\(\Rightarrow MN = \frac{1}{2}BC\).
Giải bài 2 trang 66 Toán 8 tập 2 CD
Cho tam giác $ABC$ có $AM$ là đường trung tuyến, các điểm $N, P$ phân biệt thuộc cạnh $AB$ sao cho \(AP = PN = NB\). Gọi $Q$ là giao điểm của $AM$ và $CP$. Chừng minh:
a) \(MN//CP\);
b) \(AQ = QM\);
c) \(CP = 4PQ\).
Bài giải:
Ta có hình vẽ minh họa sau:
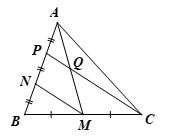
a) Vì \(AP = PN = NB\) nên $N$ là trung điểm $BP$.
Mà $M$ là trung điểm $BC$ nên $MN$ là đường trung bình của tam giác $BPC$.
Suy ra \(MN//CP\).
b) Tam giác $AMN$ có \(MN//CP\) nên:
\(\frac{{AP}}{{PN}} = \frac{{AQ}}{{QM}}\) (Định lý Thales)
Mà \(AP = PN = NB\) nên $P$ là trung điểm $AN$ hay \(\frac{{AP}}{{PN}} = 1\)
Suy ra \(\frac{{AQ}}{{QM}} = 1 \Rightarrow AQ = QM\).
c) $P$ là trung điểm $AN, Q$ là trung điểm $AM$ nên $PQ$ là đường trung bình của tam giác $AMN$.
Suy ra \(PQ = \frac{1}{2}MN\)
Mà $MN$ là đường trung bình của tam giác $BPC$ nên \(MN = \frac{1}{2}CP \Rightarrow CP = 2MN\)
Vậy \(CP = 4PQ\).
Giải bài 3 trang 66 Toán 8 tập 2 CD
Cho tứ giác $ABCD$ có $M, N, P, Q$ lần lượt là trung điểm của các cạnh $AB, BC, CD, DA$.
a) Chứng minh tứ giác $MNPQ$ là hình bình hành.
b) Cho \(AC = BD\). Chứng minh tứ giác $MNPQ$ là hình thoi.
c) Cho \(AC \bot BD\). Chứng minh tứ giác $MNPQ$ là hình chữ nhật.
Bài giải:
Ta có hình vẽ minh họa sau:
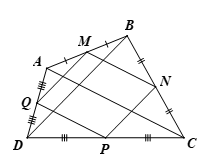
a) Vì $M$ và $N$ lần lượt là trung điểm của $AB$ và $BC$ nên $MN$ là đường trung bình của tam giác $ABC$.
\(\Rightarrow \left\{ \begin{array}{l}MN//AC\\MN = \frac{1}{2}AC\end{array} \right.\)
Vì $P$ và $Q$ lần lượt là trung điểm của $CD$ và $DA$ nên $PQ$ là đường trung bình của tam giác $ACD$.
\(\Rightarrow \left\{ \begin{array}{l}PQ//AC\\PQ = \frac{1}{2}AC\end{array} \right.\)
Khi đó \(MN//PQ\) và \(MN = PQ\).
Vậy tứ giác $MNPQ$ là hình bình hành (dhnb).
b) Vì $Q$ và $M$ lần lượt là trung điểm của $DA$ và $AB$ nên $QM$ là đường trung bình của tam giác $ABD$.
Suy ra \(QM = \frac{1}{2}BD\)
Mà \(AC = BD\) và \(MN = \frac{1}{2}AC\) nên \(QM = MN\).
Mà $MNPQ$ là hình bình hành nên khi đó $MNPQ$ là hình thoi (dhnb).
c) Ta có:
\(\left. \begin{array}{l}AC \bot BD\\QM//BD\\MN//AC\end{array} \right\} \Rightarrow QM \bot MN\)
Mà $MNPQ$ là hình bình hành nên khi đó $MNPQ$ là hình chữ nhật (dhnb).
Giải bài 4 trang 66 Toán 8 tập 2 CD
Cho tam giác $ABC$ nhọn có $H$ là trực tâm. Gọi $M, N, P, Q$ lần lượt là trung điểm của các đoạn thẳng $AB, BH, HC, CA$. Chứng minh tứ giác $MNPQ$ là hình chữ nhật.
Bài giải:
Ta có hình vẽ minh họa sau:
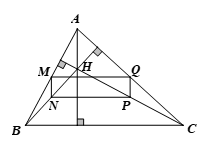
Vì $M, N$ lần lượt là trung điểm của các đoạn thẳng $AB, BH$ nên ta có:
$MN$ là đường trung bình tam giác $ABH$
\( \Rightarrow MN//AH\) mà \(AH \bot BC\) nên \(MN \bot BC\) (1)
Vì $P, Q$ lần lượt là trung điểm của các đoạn thẳng $CH, AC$ nên ta có:
$PQ$ là đường trung bình tam giác $AHC$
\( \Rightarrow PQ//AH\) mà \(AH \bot BC\) nên \(QP \bot BC\) (2)
Vì $P, N$ lần lượt là trung điểm của các đoạn thẳng $CH, BH$ nên ta có:
$PN$ là đường trung bình tam giác $BHC$
\(\Rightarrow PN//BC\) mà \(AH \bot BC\) nên \(PN \bot AH\)(3)
Vì $M, Q$ lần lượt là trung điểm của các đoạn thẳng $AB, AC$ nên ta có:
$MQ$ là đường trung bình tam giác $ABC$
\(\Rightarrow MQ//BC\) mà \(AH \bot BC\) nên \(MQ \bot AH\) (4)
Từ (1), (2), (3), (4) ta có:
\(\widehat {MNP} = \widehat {NPQ} = \widehat {PQM} = \widehat {QMN} = 90^\circ \)
Vậy tứ giác $MNPQ$ là hình chữ nhật (dhnb).
Giải bài 5 trang 66 Toán 8 tập 2 CD
Trong Hình 36, ba cạnh màu vàng $AB, BC, CA$ gợi nên hình ảnh tam giác $ABC$ và đoạn thẳng màu xanh $MN$ là một đường trung bình của tam giác đó. Bạn Duyên đứng ở phía dưới đo khoảng cách giữa hai chân cột số $(1)$ và số $(2)$, từ đó ước lượng được độ dài đoạn thẳng $MN$ khoảng $4,5m$. Khoảng cách giữa hai mép dưới cua mái được tính bằng độ dài đoạn thẳng $BC$. Hỏi khoảng cách đó bao nhiêu mét?

Bài giải:
Vì $MN$ là đường trung bình của tam giác $ABC$ nên:
\(MN = \frac{1}{2}BC \Rightarrow BC = 2MN = 2.4,5 = 9 \,m\)
Vậy khoảng cách giữa hai mép dưới của mái là $9 \,m$.
Bài trước:
👉 Giải bài 1 2 3 4 trang 60 61 sgk Toán 8 tập 2 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 trang 69 sgk Toán 8 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 trang 65 sgk Toán 8 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
