Nội Dung
Hướng dẫn giải Bài §5. Biểu diễn thập phân của một số hữu tỉ sgk Toán 7 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 trang 29 sgk Toán 7 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§5. BIỂU DIỄN THẬP PHÂN CỦA MỘT SỐ HỮU TỈ
Câu hỏi khởi động trang 27 Toán 7 tập 1 CD
Viết các số hữu tỉ \(\frac{1}{10}\) và \(\frac{1}{9}\) dưới dạng số thập phân ta được: \(\frac{1}{10}=0,1\) và \(\frac{1}{9}=0,111…\)
Hai số thập phân $0,1$ và $0,111…$ khác nhau như thế nào?
Biểu diễn thập phân của số hữu tỉ như thế nào?
Trả lời:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
– Số thập phân $0,1$ là số thập phân hữu hạn. Còn số thập phân $0,111…$ là số thập phân vô hạn tuần hoàn có chu kì là $1$. Số $0,111…$ được viết gọn là $0,(1)$.
– Mỗi số hữu tỉ \(\frac{a}{b}\) với$ a, b ∈ ℤ; b ≠ 0$ đều được biểu diễn bởi một số thập phân của hữu hạn hoặc vô hạn tuần hoàn bằng cách thực hiện phép chia $a : b$.
I. SỐ THẬP PHÂN HỮU HẠN VÀ SỐ THẬP PHÂN VÔ HẠN TUẦN HOÀN
Hoạt động 1 trang 27 Toán 7 tập 1 CD
Đặt tính để tính thương $33 : 20$.
Trả lời:
Ta đặt tính để tính thương 33 : 20 như sau:
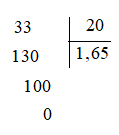
Hoạt động 2 trang 27 Toán 7 tập 1 CD
Đặt tính để tính thương $4 : 3$.
Trả lời:
Ta đặt tính để tính thương 4 : 3 như sau:
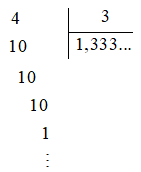
Luyện tập vận dụng trang 28 Toán 7 tập 1 CD
Sử dụng máy tính cầm tay để viết thương của mỗi phép chia sau dưới dạng số thập phân vô hạn tuần hoàn:
a) \(\frac{1}{9};\)
b)\(\frac{{ – 11}}{{45}}\)
Trả lời:
Sử dụng máy tính cầm tay, ta tính được thương của mỗi phép chia như sau:
a) \(\frac{1}{9} = 0,\left( 1 \right)\)
b) \(\frac{{ – 11}}{{45}} = – 0,2\left( 4 \right)\)
II. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 trang 29 sgk Toán 7 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 29 Toán 7 tập 1 CD
Viết mỗi phân số sau dưới dạng số thập phân hữu hạn: \(\frac{{13}}{{16}};\frac{{ – 18}}{{150}}\).
Bài giải:
Sau khi thực hiện phép chia ta viết được như sau:
\(\frac{{13}}{{16}} = 0,8125\)
\(\frac{{ – 18}}{{150}} = – 0,12\)
Vậy các phân số \(\frac{{13}}{{16}};\frac{{ – 18}}{{150}}\) viết dưới dạng số thập phân hữu hạn lần lượt là $0,8125$ và $−0,12$.
Giải bài 2 trang 29 Toán 7 tập 1 CD
Viết mỗi phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để nhận rõ chu kì): \(\frac{5}{{111}};\frac{{ – 7}}{{18}}\).
Bài giải:
Sau khi thực hiện phép chia ta viết được như sau:
\(\frac{5}{{111}} = 0,\left( {045} \right);\,\,\,\frac{{ – 7}}{{18}} = -0,3\left( 8 \right)\)
Vậy các phân số \(\frac{5}{{111}};\frac{{ – 7}}{{18}}\) viết dưới dạng số thập phân vô hạn tuần hoàn lần lượt là $0,(045)$ và $− 0,3(8)$.
Giải bài 3 trang 29 Toán 7 tập 1 CD
Viết mỗi số thập phân hữu hạn sau đây dưới dạng phân số tối giản:
a) 6,5; b) -1,28; c) -0,124.
Bài giải:
Ta viết dưới dạng phân số tối giản như sau:
a) \(6,5 = \frac{{65}}{{10}} = \frac{{13}}{2}\)
b) \( – 1,28 = \frac{{ – 128}}{{100}} = \frac{{ – 32}}{{25}}\)
c) \(-0,124 = \frac{{-124}}{{1000}} = \frac{{-31}}{{250}}\)
Giải bài 4 trang 29 Toán 7 tập 1 CD
Sử dụng máy tính cầm tay để thực hiện mỗi phép chia sau:
a) 1:999; b) 8,5:3; c) 14,2:3,3.
Bài giải:
Sử dụng máy tính cầm tay, ta tính được thương của mỗi phép chia như sau:
a) \({\rm{ }}1:999 = 0,\left( {001} \right)\)
b) \({\rm{ }}8,5:3 = 2,8\left( 3 \right)\)
c) \({\rm{ }}14,2:3,3 = 4,\left( {30} \right)\).
Bài trước:
👉 Giải bài 1 2 3 4 5 6 7 8 trang 25 26 sgk Toán 7 tập 1 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 7 8 9 10 trang 30 31 sgk Toán 7 tập 1 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 trang 29 sgk Toán 7 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
