Nội Dung
Hướng dẫn giải Bài §1. Tổng các góc của một tam giác sgk Toán 7 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 trang 72 73 sgk Toán 7 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§1. TỔNG CÁC GÓC CỦA MỘT TAM GIÁC
Câu hỏi khởi động trang 70 Toán 7 tập 2 CD
Tòa tháp Capital Gate (thuộc Các Tiểu vương quốc A-rập Thống nhất) nghiêng 18° so với phương thẳng đứng (góc nghiêng biểu diễn như Hình 1). Tính đến ngày 01/6/2020, tòa tháp này là tòa tháp nghiêng nhiều nhất trên thế giới.
(Nguồn: https://vi.wikipedia.org)

Làm thế nào để biết được độ nghiêng của tòa tháp Capital Gate so với phương nằm ngang?
Trả lời:
Để biết được độ nghiêng của tòa tháp Capital Gate so với phương nằm ngang ta xác định số đo góc được tạo bới tòa tháp và mặt đất (phương nằm ngang).
Hoạt động 1 trang 70 Toán 7 tập 2 CD
Cắt tam giác ABC thành ba mảnh (Hình 2a) và ghép lại (Hình 2b). Quan sát Hình 2b và dự đoán tổng ba góc A, B, C.
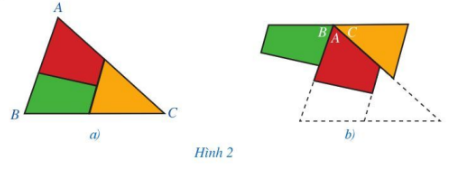
Trả lời:
Dự đoán tổng ba góc:
\(\widehat A + \widehat B + \widehat C = 180^\circ \).
Luyện tập vận dụng 1 trang 71 Toán 7 tập 2 CD
Cho tam giác đều ABC. Tính số đo mỗi góc của tam giác đó.
Trả lời:
Tam giác đều có ba góc bằng nhau do đó:
Số đo mỗi góc của tam giác đều bằng \(\dfrac{{180}}{3} = 60^\circ \).
Hoạt động 2 trang 72 Toán 7 tập 2 CD
Cho tam giác ABC vuông tại A. Tổng hai góc B và C bằng bao nhiêu độ?
Trả lời:
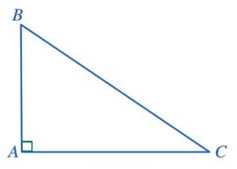
Trong tam giác ABC:
\(\widehat A + \widehat B + \widehat C = 180^\circ \)
Suy ra:
\(\widehat B + \widehat C = 180^\circ – \widehat A = 180^\circ – 90^\circ = 90^\circ\)
Vậy \(\widehat B + \widehat C = 90^\circ\)
Luyện tập vận dụng 2 trang 72 Toán 7 tập 2 CD
Trong bài toán nêu ở phần mở đầu, hãy tính độ nghiêng của tòa tháp Capital Gate so với phương nằm ngang.
Trả lời:
Góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất) là góc \(\widehat B\).
Ta có:
\(\widehat B + 90^\circ + 18^\circ = 180^\circ \) (tổng ba góc của một tam giác).
Suy ra: \(\widehat B = 180^\circ – 90^\circ – 18^\circ = 72^\circ \)
Vậy góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang có số đo là $72^\circ$.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 trang 72 73 sgk Toán 7 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 72 Toán 7 tập 2 CD
Một khung thép có dạng hình tam giác ABC với số đo các góc ở đỉnh B và đỉnh C cùng bằng 23° (Hình 9). Tính số đo của góc ở đỉnh A.
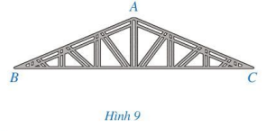
Bài giải:
Ta có: \(\widehat A + 23^\circ + 23^\circ = 180^\circ \)
Suy ra: \(\widehat A = 180^\circ – 23^\circ – 23^\circ = 134^\circ \).
Giải bài 2 trang 73 Toán 7 tập 2 CD
Hình 10 biểu diễn một chiếc cầu trượt gồm máng trượt và thang leo. Tính độ nghiêng của máng trượt so với phương thẳng đứng, biết rằng độ nghiêng của máng trượt so với mặt đất là 38°.
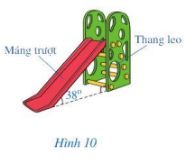
Bài giải:
Chiếc cầu trượt được minh họa và đặt tên các đỉnh như hình dưới đây:
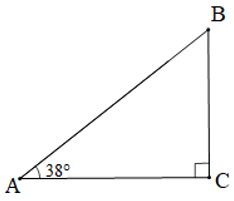
Góc tạo bởi máng trượt với phương nằm ngang (mặt đất) là: \(\widehat{BAC} = 38^0\).
Góc tạo bởi thang leo với phương nằm ngang (mặt đất) là: \(\widehat{ACB} = 90^0\).
Độ nghiêng của máng trượt so với phương thẳng đứng là: \(\widehat{ABC}\)
Xét tam giác ABC có:
\(\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180^0\) (Định lí tổng ba góc trong một tam giác)
\(\Rightarrow \widehat{ABC} + 38^0+90^0=180^0\)
\(\Rightarrow \widehat{ABC}=180^0-38^0-90^0=52^0\)
Vậy độ nghiêng của máng trượt so với phương thẳng đứng là \(52^0\).
Giải bài 3 trang 73 Toán 7 tập 2 CD
Trong Hình 11, MN // BC. Tính số đo góc C.
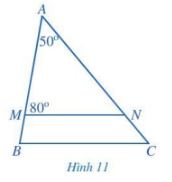
Bài giải:
Vì $MN // BC$ nên \(\widehat{ANM}=\widehat{C}\) (2 góc đồng vị)
Áp dụng định lí tổng ba góc trong tam giác AMN có:
\(\widehat{A}+\widehat{M} + \widehat{ANM}=180^0\)
\(\Rightarrow \widehat{ANM}= 180^\circ – 50^\circ – 80^\circ = 50^\circ \).
Vậy \(\widehat{C}=50^0\)
Giải bài 4 trang 73 Toán 7 tập 2 CD
Hình 12 biểu diễn mặt cắt đứng của một đường lên dốc AB. Để đo độ dốc của con đường biểu diễn bởi góc nhọn BAC tạo bới đường thẳng AB và phương nằm ngang AC, người ta làm như sau:
– Làm một thước chữ T như Hình 13;
– Đặt thước chữ T dọc theo cạnh AB như Hình 12, \(OE \bot AB\);
– Buộc một sợi dây vào chân O của thước chữ T và buộc một vật nặng vào đầu dây còn lại, sau đó thả vật nặng để sợi dây có phương thẳng đứng (trong xây dựng gọi là thả dây dọi);
– Tính góc BAC, biết rằng dây dọi OI tạo với trục OE của thước chữ T một góc 15°.
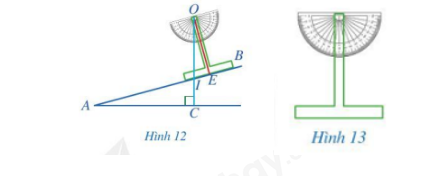
Bài giải:
Trong tam giác OIE:
\(\widehat{OIE} + \widehat{IOE} + 90^\circ = 180^\circ \)
Trong tam giác AIC:
\(\widehat{AIC} + \widehat{IAC} + 90^\circ = 180^\circ \)
Mà \(\widehat{OIE}=\widehat{AIC}\) (đối đỉnh)
\(\Rightarrow \widehat{IOE}=\widehat{IAC} \). Mà \(\widehat{IOE}=15^0\)
Vậy góc BAC bằng: \(15^\circ \).
Bài trước:
👉 Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 68 69 sgk Toán 7 tập 2 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 7 trang 76 77 sgk Toán 7 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 trang 72 73 sgk Toán 7 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
