Nội Dung
Hướng dẫn giải Bài 8. Tính chất ba đường cao của tam giác sgk Toán 7 tập 2 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 trang 78 sgk Toán 7 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
BÀI 8. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC
Hoạt động khởi động trang 77 Toán 7 tập 2 CTST
Làm thế nào để tính khoảng cách từ mỗi đỉnh đến cạnh đối diện của một tam giác?
Trả lời:
Khoảng cách từ mỗi đỉnh đến cạnh đối diện của tam giác là độ dài đường cao xuất phát từ đỉnh đến cạnh đối diện của đỉnh đó.
1. ĐƯỜNG CAO CỦA TAM GIÁC
Hoạt động khám phá 1 trang 77 Toán 7 tập 2 CTST
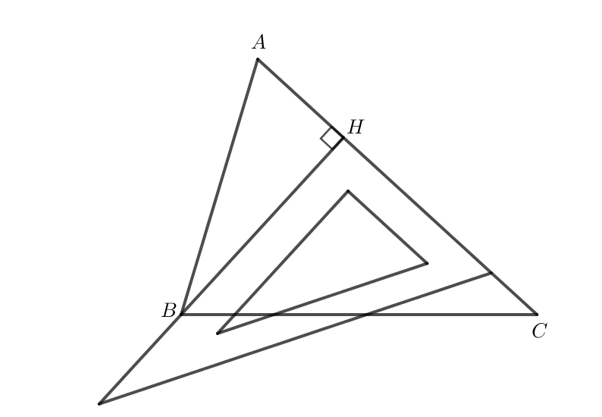
Em hãy dựng tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B đến cạnh AC của tam giác.
Trả lời:
Ta thực hiện theo các bước sau:
Bước 1. Vẽ tam giác ABC.
Bước 2. Đặt êke sao cho một cạnh của êke trùng với cạnh AC, di chuyển êke sao cho cạnh còn lại đi qua đỉnh B.
Bước 3. Khi đó kẻ một đoạn thẳng từ B đến cạnh AC thông qua cạnh của êke vừa đặt ở bước 2 ta thu được đoạn thẳng vuông góc từ đỉnh B đến cạnh AC.
Ta có hình vẽ sau:
Thực hành 1 trang 77 Toán 7 tập 2 CTST
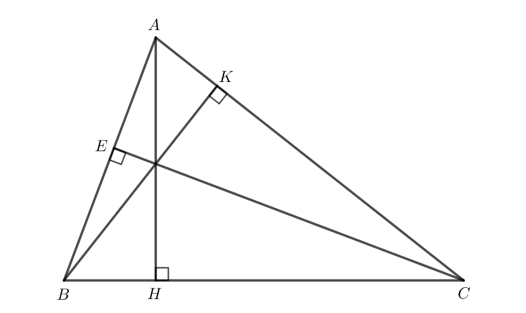
Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC.
Trả lời:
Để vẽ đường cao AH của tam giác nhọn ABC ta làm như sau:
Bước 1. Vẽ tam giác nhọn ABC.
Bước 2. Đặt êke sao cho 1 cạnh của êke trùng với cạnh BC, cạnh còn lại đi qua đỉnh A.
Khi đó kẻ 1 đường thẳng từ A đến BC thông qua cạnh đi đỉnh A vừa đặt, ta thu được đường cao đi qua đỉnh A. Đường thẳng này cắt cạnh BC tại một điểm, điểm này chính là điểm H.
Thực hiện tương tự đối với các đường cao BK và CE ta thu được hình vẽ sau:
Vận dụng 1 trang 77 Toán 7 tập 2 CTST
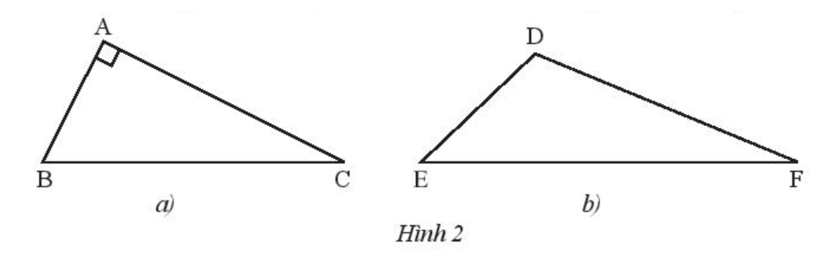
Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a).
Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b).
Trả lời:
a) Ta thấy ở tam giác ABC vuông tại A thì BA chính là đường cao từ đỉnh B của tam giác vuông ABC
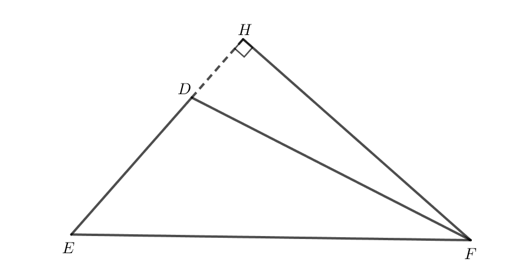
b) Ta thấy đường cao tam giác tù DEF xuất phát từ đỉnh F sẽ nằm ngoài tam giác DEF và chân đường cao nằm trên đoạn kéo dài của đoạn ED.
2. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC
Hoạt động khám phá 2 trang 77 Toán 7 tập 2 CTST
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.
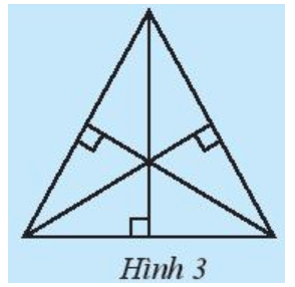
Trả lời:
Bước 1. Thực hiện đặt êke sao cho 1 cạnh của êke trùng với 1 cạnh của tam giác, cạnh còn lại đi qua đỉnh đối diện với cạnh đó. Khi đó ta thu được 1 đường cao của tam giác.
Bước 2. Thực hiện tương tự với 2 đỉnh còn lại, ta thu được 3 đường cao của tam giác.
Nhận xét: Ba đường cao cùng đi qua 1 điểm
Thực hành 2 trang 78 Toán 7 tập 2 CTST
Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc với ML.
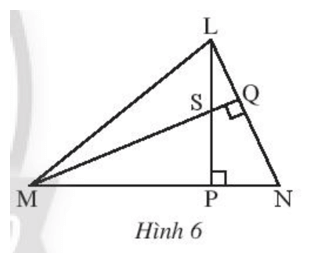
Trả lời:
Tam giác $LMN$ có hai đường cao $LP$ và $MQ$ cắt nhau tại $S$ nên $S$ là trực tâm của tam giác $LMN$.
Do đó $NS ⊥ ML$.
Vận dụng 2 trang 78 Toán 7 tập 2 CTST
Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
Trả lời:
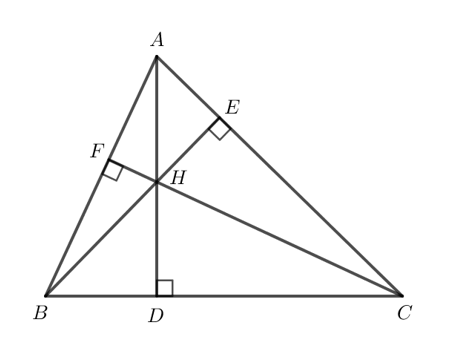
Tam giác $HBC$ có $HD ⊥ BC, BF ⊥ HC$ nên $HD$ và $BF$ là hai đường cao của tam giác $HBC$.
Mà $HD$ và $BF$ cắt nhau tại $A$ nên $A$ là trực tâm của tam giác $HBC$.
Tam giác $HAB$ có $HF ⊥ AB, BD ⊥ AH$ nên $HF, BD$ là hai đường cao của tam giác $HAB$.
Mà $HF$ và $BD$ cắt nhau tại $C$ nên $C$ là trực tâm của tam giác $HAB$.
Tam giác $HAC$ có $HE ⊥ AC, CD ⊥ AH$ nên $HE, CD$ là hai đường cao của tam giác $HAC$.
Mà HE và CD cắt nhau tại B nên B là trực tâm của tam giác HAC.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 trang 78 sgk Toán 7 tập 2 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 78 Toán 7 tập 2 CTST
Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.
Bài giải:
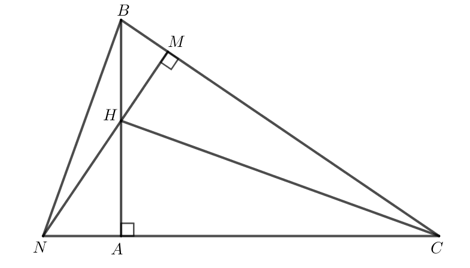
Tam giác $BNC$ có $BA ⊥ NC, NM ⊥ BC$ nên $BA, NM$ là hai đường cao của tam giác $BNC$.
Mà $BA$ và $NM$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $BNC$.
Do đó $CH ⊥ NB$.
Giải bài 2 trang 78 Toán 7 tập 2 CTST
Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho $BM = BC$. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
Bài giải:
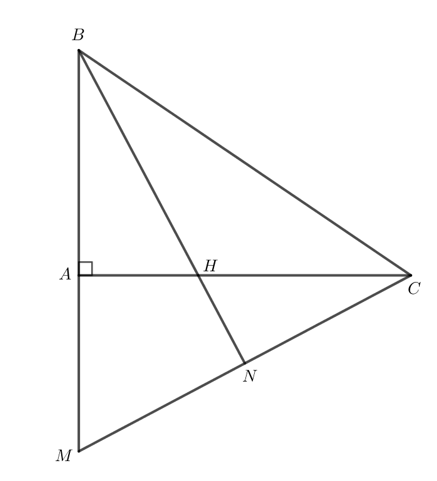
Tam giác $BMC$ có $BM = BC$ nên tam giác $BMC$ cân tại $B$.
Tam giác $BMC$ cân tại $B$, có $BN$ là đường phân giác nên $BN$ cũng là đường cao của tam giác $BMC$.
Do đó $BN ⊥ MC$.
Tam giác $BMC$ có $CA ⊥ BM, BN ⊥ MC$ nên $CA, BN$ là hai đường cao của tam giác $BMC$.
Mà $CA$ và $BN$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $BMC$.
Do đó $MH ⊥ BC$.
Giải bài 3 trang 78 Toán 7 tập 2 CTST
Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho $AD = AE$. Chứng minh rằng:
a) DE vuông góc với BC.
b) BE vuông góc với DC.
Bài giải:
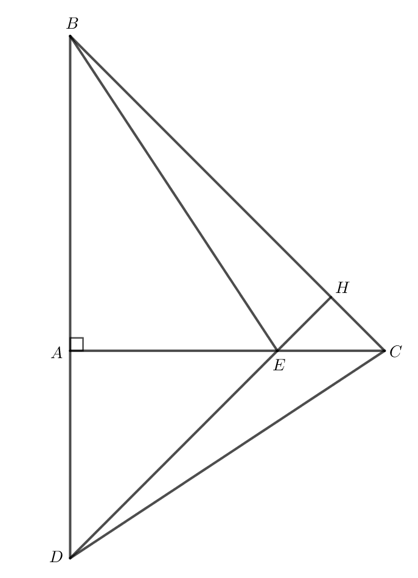
a) Vì tam giác $ABC$ vuông cân tại $A$
⇒ \(\widehat B = \widehat C = {45^o}\) (2 góc ở đáy bằng nhau)
Xét tam giác $AED$ có:
$AE = AD$
$AC ⊥ AB$
⇒ Tam giác $AED$ vuông cân tại $A$
\(⇒ \widehat {ADE} = \widehat {AED} = {45^o}\)
Mà \(\widehat {AED}; \widehat {CEH}\) là 2 góc đối đỉnh \(⇒ \widehat {AED} = \widehat {CEH} = {45^o}\)
Áp dụng định lí tổng 3 góc trong tam giác CEH ta có:
\(\widehat H + \widehat C + \widehat E = {180^o}\)
$⇒ \widehat H = {180^o} – {45^o} – {45^o} = {90^o}$
$⇒ EH \bot BC$
$⇒ DE \bot BC$.
b) Vì $DE$ vuông góc với $BC ⇒ DE$ là đường cao của tam giác $BCD$
Mà $AC$ cắt $DE$ tại $E$ nên $E$ là trực tâm tam giác $BCD$ (Do $AC$ cũng là đường cao của tam giác $BCD$)
Suy ra BE cũng là đường cao của tam giác $BCD$ (định lí 3 đường cao trong tam giác đi qua trực tâm)
$⇒BE ⊥ DC$.
Giải bài 4 trang 78 Toán 7 tập 2 CTST
Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết $AD = BE = CF$. Chứng minh rằng tam giác ABC đều.
Bài giải:
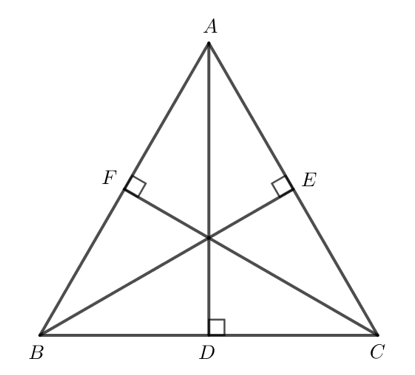
Xét tam giác $BFC$ và tam giác $BEC$ có:
$BC$ chung
$FC = BE$
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
⇒ $∆BFC = ∆BEC$ (cạnh huyền – cạnh góc vuông)
\(⇒ \widehat C = \widehat B\) (2 góc tương ứng ) (1)
Xét tam giác $CFA$ và tam giác $ADC$ ta có:
$CF = AD$
$AC$ chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
⇒ $∆CFA = ∆ADC$ (cạnh huyền – cạnh góc vuông)
\(⇒ \widehat C = \widehat A\) (2 góc tương ứng ) (2)
Từ (1) và (2) \(⇒ \widehat C = \widehat A = \widehat B\)
Suy ra tam giác $ABC$ là tam giác đều (do có 3 góc bằng nhau).
Bài trước:
👉 Giải bài 1 2 3 4 5 6 trang 75 76 sgk Toán 7 tập 2 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 trang 81 82 sgk Toán 7 tập 2 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 trang 78 sgk Toán 7 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
