Nội Dung
Hướng dẫn giải Bài §3. Hai tam giác bằng nhau sgk Toán 7 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 trang 79 sgk Toán 7 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§3. HAI TAM GIÁC BẰNG NHAU
Câu hỏi khởi động trang 78 Toán 7 tập 2 CD
Một dây chuyền sản xuất ra các sản phẩm có dạng hình tam giác giống hệt nhau (Hình 27). Khi đóng gói hàng, người ta xếp chúng chồng khít lên nhau.

Khi hai tam giác có thể chồng khít lên nhau thì các cạnh và các góc tương ứng liên hệ với nhau như thế nào?
Trả lời:
Khi hai tam giác có thể trồng khít lên nhau thì các cạnh tương ứng của hai tam giác bằng nhau và các góc tương ứng của hai tam giác bằng nhau.
Hoạt động 1 trang 78 Toán 7 tập 2 CD
Dùng kéo cắt tờ giấy thứ nhất thành hình tam giác ABC. Đặt hình tam giác ABC lên tờ giấy thứ hai, vẽ theo các cạnh của hình tam giác ABC trên tờ giấy thứ hai rồi cắt thành hình tam giác A’B’C’ (Hình 28).

Sau khi đặt tam giác ABC chồng khít lên tam giác A’B’C’, hãy so sánh:
a) Các cạnh tương ứng: AB và A’B’; BC và B’C’; CA và C’A’;
b) Các góc tương ứng: \(\widehat A\) và \(\widehat {A’}\); \(\widehat B\) và \(\widehat {B’}\); \(\widehat C\) và \(\widehat {C’}\).
Trả lời:
Sau khi đặt tam giác ABC chồng khít lên tam giác A’B’C’ ta thấy:
a) $AB = A’B’; BC = B’C’; CA = C’A’$.
b) \(\widehat A = \widehat {A’}\); \(\widehat B = \widehat {B’}\); \(\widehat C = \widehat {C’}\).
Hoạt động 2 trang 79 Toán 7 tập 2 CD
Quan sát hai tam giác ABC và A’B’C’ trên một tờ giấy kẻ ô vuông (Hình 30).

a) So sánh:
– Các cặp cạnh: AB và A’B’; BC và B’C’; CA và C’A’.
– Các cặp góc: A và A’; B và B’; C và C’.
b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không?
c) Cắt mảnh giấy hình tam giác ABC và mảnh giấy hình tam giác A’B’C’, hai hình tam giác đó có thể đặt chồng khít lên nhau hay không?
Trả lời:
Quan sát hình trên ta thấy:
a) $AB = A’B’; BC = B’C’; CA = C’A’$.
\(\widehat A = \widehat {A’}\); \(\widehat B = \widehat {B’}\); \(\widehat C = \widehat {C’}\).
b) Hai tam giác ABC và A’B’C’ có bằng nhau vì chúng có các cặp cạnh và cặp góc tương ứng bằng nhau.
c) Hai hình tam giác ABC và A’B’C’ có thể đặt chồng khít lên nhau.
Luyện tập vận dụng trang 79 Toán 7 tập 2 CD
Cho biết \(\Delta ABC = \Delta MNP\), \(AC = 4\) cm, \(\widehat {MPN} = 45^\circ \). Tính độ dài cạnh MP và số đo góc ACB.
Trả lời:
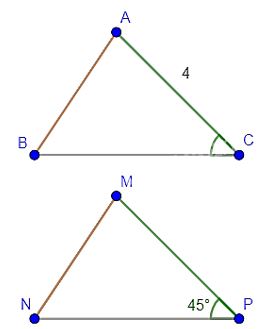
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\) và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\) cm và \(\widehat {ACB} = 45^\circ \).
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 trang 79 sgk Toán 7 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 79 Toán 7 tập 2 CD
Cho biết \(\Delta ABC = \Delta DEG\), \(AB = 3\) cm, \(BC = 4\) cm, \(CA = 6\) cm. Tìm độ dài các cạnh của tam giác DEG.
Bài giải:
Vì \(\Delta ABC = \Delta DEG\) nên $AB = DE, BC = EG, CA = GD$.
Vậy độ dài các cạnh của tam giác DEG lần lượt là: \(DE = 3\) cm, \(EG = 4\) cm, \(GD = 6\) cm.
Giải bài 2 trang 79 Toán 7 tập 2 CD
Cho biết \(\Delta PQR = \Delta IHK\), \(\widehat P = 71^\circ, \widehat Q = 49^\circ \). Tính số đo góc K của tam giác IHK.
Bài giải:
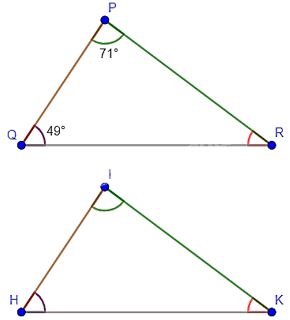
Ta có:
\(\Delta PQR = \Delta IHK\) nên \(\widehat P = \widehat I; \widehat Q = \widehat H; \widehat R = \widehat K\).
\(⇒ \widehat I = 71^\circ ,\widehat H = 49^\circ \).
Mà tổng 3 góc trong một tam giác bằng 180° nên trong tam giác IHK:
\(\widehat I + \widehat H + \widehat K = 180^\circ \)
Vậy \(\widehat K = 180^\circ – 71^\circ – 49^\circ = 60^\circ \).
Giải bài 3 trang 79 Toán 7 tập 2 CD
Cho \(\Delta ABC = \Delta MNP\) và \(\widehat A + \widehat N = 125^\circ \). Tính số đo góc P.
Bài giải:
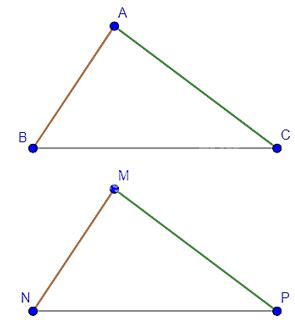
Ta có:
\(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Mà \(\widehat A + \widehat N = 125^\circ \) hay \(\widehat M + \widehat N = 125^\circ \). Tổng ba góc trong một tam giác bằng 180°.
Trong tam giác MNP:
$\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ + \widehat P = 180^\circ \\ \to \widehat P = 180^\circ – 125^\circ = 55^\circ $
Vậy số đo góc P là 55°.
Giải bài 4 trang 79 Toán 7 tập 2 CD
Cho tam giác ABC và điểm M thuộc cạnh BC thỏa mãn \(\Delta AMB = \Delta AMC\)(Hình 32). Chứng minh rằng:
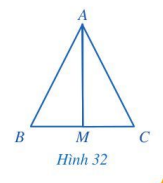
a) M là trung điểm của đoạn thẳng BC.
b) Tia AM là tia phân giác của góc BAC và \(AM \bot BC\).
Bài giải:
a) Ta có:
\(\Delta AMB = \Delta AMC\) nên AB = AC, MB = MC nên M là trung điểm của đoạn thẳng BC.
b) Ta có:
\(\Delta AMB = \Delta AMC\) nên \(\widehat {AMB} = \widehat {AMC}, \widehat {MAB} = \widehat {MAC}, \widehat {MBA} = \widehat {MCA}\).
Vậy tia AM là tia phân giác của góc BAC vì \(\widehat {MAB} = \widehat {MAC}\).
Ta thấy:
\(\widehat {AMB} = \widehat {AMC}\) mà ba điểm B, M, C thẳng hàng nên \(\widehat {BMC} = 180^\circ \).
\(⇒ \widehat {AMB} = \widehat {AMC} = \dfrac{1}{2}.\widehat {BMC} = \dfrac{1}{2}.180^\circ = 90^\circ \).
Vậy \(AM \bot BC\).
Bài trước:
👉 Giải bài 1 2 3 4 5 6 7 trang 76 77 sgk Toán 7 tập 2 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 trang 83 sgk Toán 7 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 trang 79 sgk Toán 7 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
