Nội Dung
Hướng dẫn giải Bài §2. Tứ giác sgk Toán 8 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 trang 100 sgk Toán 8 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
§2. TỨ GIÁC
Câu hỏi khởi động trang 98 Toán 8 tập 1 CD
Hình ảnh thửa ruộng nhìn từ trên cao hay hình ảnh cánh diều (Hình 12) gợi lên những hình tứ giác.
Tứ giác là hình có những tính chất gì?
Trả lời:
Sau bài học này chúng ta giải quyết được câu hỏi trên như sau:
Tứ giác là hình có 4 cạnh, 2 đường chéo, 4 đỉnh và 4 góc trong đó:
– Hai cạnh kề nhau không cùng thuộc một đường thẳng.
– Không có ba đỉnh nào thẳng hàng.
– Tổng các góc của tứ giác bằng 360°.
I. TỨ GIÁC
Hoạt động 1 trang 98 Toán 8 tập 1 CD
Quan sát tứ giác ABCD ở Hình 13 và đọc tên các cạnh, các đường chéo, các đỉnh, các góc của tứ giác đó.

Trả lời:
Tứ giác $ABCD$ có:
– Các cạnh: $AB, BC, CD, DA$.
– Các đường chéo: $AC, BD$.
– Các đỉnh: $A, B, C, D$.
– Các góc: \(\widehat {DAB}, \widehat {ABC}, \widehat {BC{\rm{D}}}, \widehat {C{\rm{D}}A}\).
Hoạt động 2 trang 98 Toán 8 tập 1 CD
Quan sát các hình 14a, 14b và nêu nhận xét về vị trí của mỗi tứ giác so với đường thẳng chứa một cạnh bất kì của tứ giác đó.

Trả lời:
Hình 14a: Tứ giác $ABCD$ luôn nằm về 1 phía của 1 cạnh bất kì.
Hình 14b: Tứ giác $MNPQ$ nằm về 2 phía của đường thẳng chứa cạnh $PQ$, cạnh $MN$. Hoặc tứ giác $MNPQ$ không nằm về một phía của đường thẳng chứa cạnh $NP$ hoặc cạnh $PQ$ của tứ giác.
II. TỔNG CÁC GÓC CỦA MỘT TỨ GIÁC
Hoạt động 3 trang 99 Toán 8 tập 1 CD
Quan sát tứ giác ABCD ở Hình 16, đường chéo AC chia nó thành hai tam giác ABC và ACD.

a) Gọi $T_1$ và $T_2$ lần lượt là tổng các góc của tam giác ABC và tam giác ACD. Tổng $T_1 + T_2$ bằng bao nhiêu độ?
b) Gọi $T$ là tổng các góc của tứ giác ABCD. So sánh $T$ với $T_1 + T_2$.
Trả lời:
a) Ta có:
\({T_1} = {180^o}\) (tổng 3 góc của \(\Delta ABC\))
\({T_2} = {180^o}\) (tổng 3 góc của \(\Delta ACD\))
Suy ra:
\({T_1} + {T_2} = {180^o} + {180^o} = {360^o}\)
b) Xét tứ giác ABCD ta có:
$T = \widehat {A} + \widehat {B} + \widehat {C}+ \widehat {D} = {360^o}$
$⇒T = {T_1} + {T_2} = {360^o}$.
Luyện tập vận dụng trang 100 Toán 8 tập 1 CD
Tìm $x$ trong Hình 18.
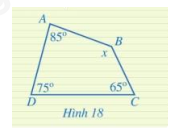
Trả lời:
Xét tứ giác $ABCD$ có:
$\widehat {A} + \widehat {B} + \widehat {C}+ \widehat {D} = {360^0}$
$⇔ {85^o} + x + {65^o} + {75^o} = {360^o}$
$⇒x = {360^o} – {85^o} – {65^o} – {75^o} = {135^o}$
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 trang 100 sgk Toán 8 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 100 Toán 8 tập 1 CD
Trong các tứ giác ở hình 19a, 19b, 19c, 19d, 19e, 19g, tứ giác nào không phải là tứ giác lồi? Vì sao?

Bài giải:
Tứ giác ở Hình 19c không phải là tứ giác lồi vì: Tứ giác hình 19c nằm về 2 phía của diện tích tứ giác chứa 1 cạnh bất kì.
Giải bài 2 trang 100 Toán 8 tập 1 CD
a) Tứ giác ABCD có \(\widehat A + \widehat B = {180^o}\) thì \(\widehat B + \widehat D\) bằng bao nhiêu độ?
b) Có hay không một tứ giác có 2 góc tù và 2 góc vuông?
c) Có hay không một tứ giác có cả 4 góc đều là góc nhọn?
Bài giải:
a) Xét tứ giác $ABCD$ có:
$\widehat {A} + \widehat {B} + \widehat {C}+ \widehat {D} = {360^o}$
Mà \(\widehat A + \widehat B = {180^o}\) nên:
\(\widehat B + \widehat D = {360^0} – {180^o} = {180^o}\)
b) Vì tổng 2 góc tù lớn hơn \({180^0}\), tổng 2 góc vuông bằng \({180^0}\)
Suy ra: Tổng 4 góc của tứ giác lớn hơn \({360^0}\) (không tồn tại)
Vậy không có 1 tứ giác có 2 góc tù và 2 góc vuông.
c) Vì góc nhọn có số đo nhỏ hơn \({90^0}\) nên tổng số đo 4 góc nhọn nhỏ hơn \({360^0}\)
Vậy không tồn tại 1 tứ giác nào có 4 góc đều là góc nhọn.
Giải bài 3 trang 100 Toán 8 tập 1 CD
Hình 20 mô tả mặt cắt dọc phần nổi trên mặt nước của một chiếc tàu thuỷ. Tính chu vi mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thuỷ đó (làm tròn kết quả đến hàng phần mười của mét).
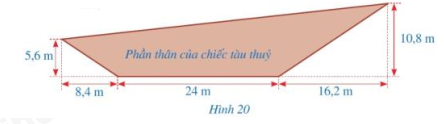
Bài giải:
Giả sử mặt cắt dọc phần nổi trên mặt nước cả tàu thủy được mô tả như hình vẽ dưới đây:
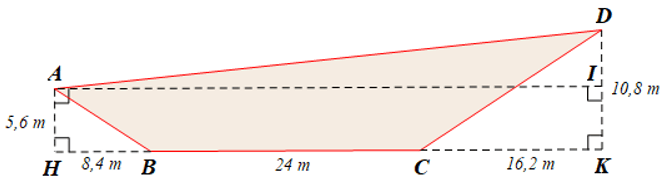
♦ Do tam giác $AHB$ vuông tại $H$ nên theo định lí Pythagore ta có:
$AB^2 = AH^2 + HB^2 = 5,6^2 + 8,4^2 \\= 31,36 + 70,56 = 101,92$
Suy ra $AB = \sqrt {101,92} (m)$
♦ Do tam giác $CDK$ vuông tại $K$ nên theo định lí Pythagore ta có:
$CD^2 = CK^2 + KD^2 = 16,2^2 + 10,8^2 \\= 262,44 + 116,64 = 379,08$
Suy ra $CD = \sqrt {379,08} (m)$
♦ Ta lại có
$AI = HK = HB + BC + CK \\= 8,4 + 24 + 16,2 = 48,6 (m)$
$DI = DK – IK = DK – AH \\= 10,8 – 5,6 = 5,2 (m)$
Do tam giác $ADI$ vuông tại $I$ nên theo định lí Pythagore ta có:
$AD^2 = AI^2 + DI^2 = 48,6^2 + 5,2^2 \\= 2 361,96 + 27,04 = 2 389$
Suy ra $AD = \sqrt {2 389} (m)$
♦ Chu vi mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thuỷ đó là:
$AB + BC + CD + DA$ $= \sqrt {101,92} + 24 + \sqrt {379,08} + \sqrt {2389} \approx 102,4$
Vậy chu vi của mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thủy là $102,4 m$.
Bài trước:
👉 Giải bài 1 2 3 4 5 6 trang 96 97 sgk Toán 8 tập 1 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 trang 103 104 sgk Toán 8 tập 1 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 trang 100 sgk Toán 8 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
