Nội Dung
Hướng dẫn giải Bài Luyện tập chung sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 18 19 20 21 22 23 trang 17 18 sgk Toán 8 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
GIẢI BÀI TẬP LUYỆN TẬP CHUNG
Sau đây là phần Giải bài 18 19 20 21 22 23 trang 17 18 sgk Toán 8 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1.18 trang 17 Toán 8 tập 1 KNTT
Cho các biểu thức:
\(\dfrac{4}{5}x; \,\left( {\sqrt 2 – 1} \right)xy; \,- 3x{y^2}; \,\dfrac{1}{2}{x^2}y; \\\dfrac{1}{x}{y^3}; \,- xy + \sqrt 2 ; \,\dfrac{{ – 3}}{2}{x^2}y; \,\dfrac{{\sqrt x }}{5}.\)
a) Trong các biểu thức đã cho, biểu thức nào là đơn thức? Biểu thức nào không là đơn thức?
b) Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.
c) Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.
Bài giải:
a) Các đơn thức là:
\(\dfrac{4}{5}x; \,\left( {\sqrt 2 – 1} \right)xy; \,- 3x{y^2};\dfrac{1}{2}{x^2}y; \,\dfrac{{ – 3}}{2}{x^2}y.\)
b) • Xét đơn thức \(\dfrac{4}{5}x\) có hệ số là \(\dfrac{4}{5}\), phần biến là \(x\).
• Xét đơn thức \(\left( {\sqrt 2 – 1} \right)xy\) có hệ số là \(\sqrt 2 – 1\), phần biến \(xy\).
• Xét đơn thức \( – 3x{y^2}\) có hệ số là \( – 3\), phần biến là \(x{y^2}\).
• Xét đơn thức \(\dfrac{1}{2}{x^2}y\) có hệ số là \(\dfrac{1}{2}\), phần biến \({x^2}y\).
• Xét đơn thức \( – \dfrac{3}{2}{x^2}y\) có hệ số là \( – \dfrac{3}{2}\), phần biến \({x^2}y\).
c) Tổng các đơn thức trên là đa thức:
$\dfrac{4}{5}x + \left( {\sqrt 2 – 1} \right)xy + \left( { – 3x{y^2}} \right) + \dfrac{1}{2}{x^2}y + \dfrac{{ – 3}}{2}{x^2}y\\ = \dfrac{4}{5}x + \left( {\sqrt 2 – 1} \right)xy – 3x{y^2} + \left( {\dfrac{1}{2} + \dfrac{{ – 3}}{2}} \right){x^2}y\\ = \dfrac{4}{5}x + \left( {\sqrt 2 – 1} \right)xy – 3x{y^2} – {x^2}y$
Bậc của đa thức trên là $1+2=3$.
Giải bài 1.19 trang 18 Toán 8 tập 1 KNTT
Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có chiều sâu là $1,2$ m, đáy là hình chữ nhật có chiều dài $x$ mét, chiều rộng $y$ mét. Bể thứ hai có chiều sâu là $1,5$ m, hai kích thước đáy gấp $5$ lần hai kích thước đáy của bể thứ nhất.
a) Hãy tìm đơn thức (hai biến $x$ và $y$) biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi.
b) Tính lượng nước bơm đầy hai bể nếu $x=5 m, \,y=3 m$.
Bài giải:
a) Ta có:
Biểu thức biểu thị số mét khối nước cần có để bơm đầy bể thứ nhất là:
${V_1} = 1,2.x.y\left( {{m^3}} \right)$
Biểu thức biểu thị số mét khối nước cần có để bơm đầy bể thứ hai là:
${V_2} = 1,5.5x.5y = 37,5.x.y\left( {{m^3}} \right)$
⇒ Biểu thức biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi:
\(V = {V_1} + {V_2} = 1,2xy + 37,5xy = \left( {1,2 + 37,5} \right)xy = 38,7xy\left( {{m^3}} \right).\)
b) Thay $x=5, \,y=3$ vào biểu thức $V$ ta được:
\(V = 38,7.5.3 = 580,5\left( {{m^3}} \right)\)
Vậy lượng nước bơm đầy hai bể nếu $x = 5 m, \,y= 3 m$ là \(580,5\,{m^3}\).
Giải bài 1.20 trang 18 Toán 8 tập 1 KNTT
Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại $x = 1; \,y = -2$.
$P = 5{x^4} – 3{x^3}y + 2x{y^3} – {x^3}y + 2{y^4} – 7{x^2}{y^2} – 2x{y^3}$;
$Q = {x^3} + {x^2}y + x{y^2} – {x^2}y – x{y^2} – {x^3}.$
Bài giải:
Ta có:
$P = 5{x^4} – 3{x^3}y + 2x{y^3} – {x^3}y + 2{y^4} – 7{x^2}{y^2} – 2x{y^3}\\ = 5{x^4} + 2{y^4} + \left( { – 3{x^3}y – {x^3}y} \right) + \left( {2x{y^3} – 2x{y^3}} \right) – 7{x^2}{y^2}\\ = 5{x^4} + 2{y^4} – 4{x^3}y – 7{x^2}{y^2}$
Ta có:
$Q = {x^3} + {x^2}y + x{y^2} – {x^2}y – x{y^2} – {x^3}\\ = \left( {{x^3} – {x^3}} \right) + \left( {{x^2}y – {x^2}y} \right) + \left( {x{y^2} – x{y^2}} \right)\\ = 0$
Do đó, bậc của đa thức $P$ là $4$; đa thức $Q$ không có bậc.
Tại $x = 1; \,y = -2$, ta có:
♦ $P = 5.{1^4} + 2{(-2)^4} – 4.{1^3}(-2) – 7.{1^2}{(-2)^2}\\=5+2.16-4.(-2)-7.4=5+32+8-28\\=17$
♦ \(Q = 0\).
Giải bài 1.21 trang 18 Toán 8 tập 1 KNTT
Cho hai đa thức:
\(A = 7xy{z^2} – 5x{y^2}z + 3{x^2}yz – xyz + 1;\\B = 7{x^2}yz – 5x{y^2}z + 3xy{z^2} – 2.\)
a) Tìm đa thức $C$ sao cho $A-C=B$;
b) Tìm đa thức $D$ sao cho $A+D=B$;
c) Tìm đa thức $E$ sao cho $E-A=B$;
Bài giải:
a) Ta có:
$A – C = B\\ ⇒ C = A – B \\= 7xy{z^2} – 5x{y^2}z + 3{x^2}yz – xyz + 1 – \left( {7{x^2}yz – 5x{y^2}z + 3xy{z^2} – 2} \right)\\ = 7xy{z^2} – 5x{y^2}z + 3{x^2}yz – xyz + 1 – 7{x^2}yz + 5x{y^2}z – 3xy{z^2} + 2\\ = \left( {7xy{z^2} – 3xy{z^2}} \right) + \left( { – 5x{y^2}z + 5x{y^2}z} \right) + \left( {3{x^2}yz – 7{x^2}yz} \right) – xyz + \left( {1 + 2} \right)\\ = 4xy{z^2} – 4{x^2}yz – xyz + 3$
b) Ta có:
$A + D = B\\ ⇒ D = B – A \\= – \left( {A – B} \right) = – C \\= – 4xy{z^2} + 4{x^2}yz + xyz – 3.$
c) Ta có:
$E – A = B\\ ⇒ E = A + B\\= 7xy{z^2} – 5x{y^2}z + 3{x^2}yz – xyz + 1 + 7{x^2}yz – 5x{y^2}z + 3xy{z^2} – 2\\ = \left( {7xy{z^2} + 3xy{z^2}} \right) + \left( { – 5x{y^2}z – 5x{y^2}z} \right) + \left( {3{x^2}yz + 7{x^2}yz} \right) – xyz + \left( {1 – 2} \right)\\ = 10xy{z^2} – 10x{y^2}z + 10{x^2}yz – xyz – 1$
Giải bài 1.22 trang 18 Toán 8 tập 1 KNTT
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính $x$ centimet và $y$ centimet. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu biết miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (centimet) như Hình 1.2. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?
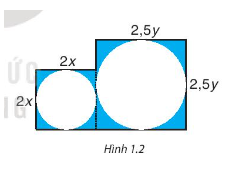
Bài giải:
Diện tích hai hình vuông là:
\(2x.2x + 2,5y.2,5y = 4{x^2} + 6.25{y^2}\)
Diện tích hai hình tròn là:
\({\pi .{x^2} + \pi .{y^2}}\)
Diện tích phần còn lại của miếng bìa là:
$S = 4{x^2} + 6.25{y^2} – \pi .{x^2} – \pi .{y^2}\\ = \left( {4 – \pi } \right){x^2} + \left( {6,25 – \pi } \right){y^2}$
Biểu thức này là một đa thức, có bậc là $2$.
Giải bài 1.23 trang 18 Toán 8 tập 1 KNTT
Cho ba đa thức:
$M = 3{x^3} – 4{x^2}y + 3x – y$;
$N = 5xy – 3x + 2$;
$P = 3{x^3} + 2{x^2}y + 7x – 1$.
Tính $M + N – P$ và $M – N – P$.
Bài giải:
Ta có:
$M + N – P = 3{x^3} – 4{x^2}y + 3x – y + 5xy – 3x + 2 – \left( {3{x^3} + 2{x^2}y + 7x – 1} \right)\\ = 3{x^3} – 4{x^2}y + 3x – y + 5xy – 3x + 2 – 3{x^3} – 2{x^2}y – 7x + 1\\ = \left( {3{x^3} – 3{x^3}} \right) + \left( { – 4{x^2}y – 2{x^2}y} \right) + 5xy + \left( {3x – 3x – 7x} \right) – y + \left( {2 + 1} \right)\\ = – 6{x^2}y + 5xy – 7x – y + 3.$
Ta có:
$M – N – P = 3{x^3} – 4{x^2}y + 3x – y – \left( {5xy – 3x + 2} \right) – \left( {3{x^3} + 2{x^2}y + 7x – 1} \right)\\ = 3{x^3} – 4{x^2}y + 3x – y – 5xy + 3x – 2 – 3{x^3} – 2{x^2}y – 7x + 1\\ = \left( {3{x^3} – 3{x^3}} \right) + \left( { – 4{x^2}y – 2{x^2}y} \right) – 5xy + \left( {3x + 3x – 7x} \right) – y + \left( { – 2 + 1} \right)\\ = – 6{x^2}y – 5xy – x – y – 1.$
Bài trước:
👉 Giải bài 14 15 16 17 trang 16 sgk Toán 8 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 24 25 26 27 28 29 trang 21 sgk Toán 8 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 18 19 20 21 22 23 trang 17 18 sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
