Nội Dung
Hướng dẫn giải Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác sgk Toán 7 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 20 21 22 23 24 25 trang 76 sgk Toán 7 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
BÀI 34. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TUYẾN, BA ĐƯỜNG PHÂN GIÁC TRONG MỘT TAM GIÁC
Bài toán mở đầu trang 72 Toán 7 tập 2 KNTT
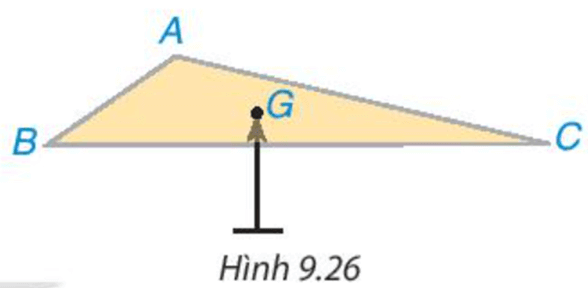
Hình 9.26 mô phỏng một miếng bìa hình tam giác ABC đặt thăng bằng trên giá nhọn tại điểm G. Điểm đó được xác định như thế nào và có gì đặc biệt?
Trả lời:
Điểm $G$ là giao điểm ba đường trung tuyến của $∆ABC$ và $G$ là trọng tâm của $∆ABC$.
1. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TUYẾN TRONG MỘT TAM GIÁC
Câu hỏi trang 72 Toán 7 tập 2 KNTT
Mỗi tam giác có mấy đường trung tuyến?
Trả lời:
Tương ứng với mỗi đỉnh của tam giác có $1$ đường trung tuyến nên mỗi tam giác có $3$ đường trung tuyến.
Hoạt động 1 trang 72 Toán 7 tập 2 KNTT
Hãy lấy một mảnh giấy hình tam giác, gấp giấy đánh dấu trung điểm của các cạnh. Sau đó, gấp giấy để được các nếp gấp đi qua đỉnh và trung điểm của cạnh đối diện (tức là các đường trung tuyến của tam giác). Mở tờ giấy ra, quan sát và cho biết ba nếp gấp (ba đường trung tuyến) có cùng đi qua một điểm không?

Trả lời:
Ba nếp gấp (ba đường trung tuyến) cùng đi qua một điểm.
Hoạt động 2 trang 73 Toán 7 tập 2 KNTT
Trên mảnh giấy kẻ ô vuông, mỗi chiều 10 ô, hãy đếm dòng, đánh dấu các đỉnh A,B,C rồi vẽ tam giác ABC (H.9.29).
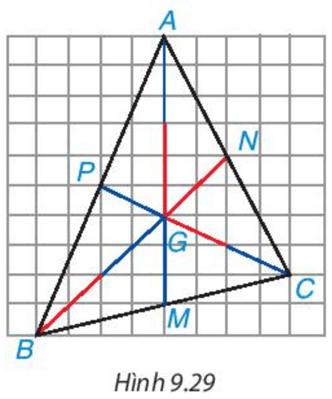
Vẽ hai đường trung tuyến BN, CP, chúng cát nhau tại G, tia AG cắt cạnh BC tại M.
• AM có phải là đường trung tuyến của tam giác ABC không?
• Hãy xác định các tỉ số \(\dfrac{{GA}}{{MA}}; \dfrac{{GB}}{{NB}}; \dfrac{{GC}}{{PC}}\).
Trả lời:
• Ta có: $MB = MC$ và $M$ nằm giữa $B$ và $C$ nên $M$ là trung điểm của $BC$.
Do đó, $AM$ có là đường trung tuyến của tam giác $ABC$.
• Ta có:
$\dfrac{{GA}}{{MA}} = \dfrac{6}{9} = \dfrac{2}{3};\\\dfrac{{GB}}{{NB}} = \dfrac{2}{3};\\\dfrac{{GC}}{{PC}} = \dfrac{2}{3}$.
Luyện tập 1 trang 73 Toán 7 tập 2 KNTT
Trong tam giác ABC ở ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB.
Trả lời:
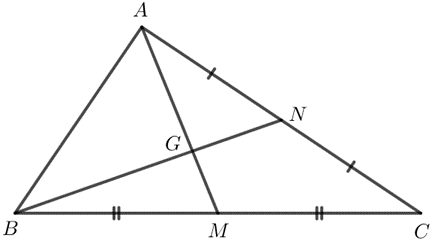
Vì $G$ là trọng tâm của tam giác $ABC$ nên:
\(\dfrac{{GB}}{{NB}} = \dfrac{2}{3} \Leftrightarrow GB = \dfrac{2}{3}NB\)
Ta có:
\(GN = NB – GB = NB – \dfrac{2}{3}NB = \dfrac{1}{3}NB\)
Mà $GN = 1 cm$ nên \(1 = \dfrac{1}{3}.NB \Rightarrow NB = 3\) (cm)
\(GB = \dfrac{2}{3}NB = \dfrac{2}{3}.3 = 2\) (cm)
Vậy $GB = 2 cm, NB = 3 cm$.
Tranh luận trang 74 Toán 7 tập 2 KNTT

Trả lời:
♦ Cách 1:
Tìm giao điểm của $2$ đường trung tuyến.
♦ Cách 2:
Vẽ 1 đường trung tuyến. Lấy điểm G cách đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh đó. Ta được $G$ là trọng tâm tam giác.
Vận dụng 1 trang 74 Toán 7 tập 2 KNTT
Trong tình huống mở đầu, người ta chứng minh được $G$ chính là trọng tâm của tam giác $ABC$. Em hãy cắt một mảnh bìa hình tam giác. Xác định trọng tâm của tam giác và đặt mảnh bìa đó lên một giá nhọn tại trọng tâm vừa xác định. Quan sát xem mảnh bìa có thăng bằng không.
Trả lời:
Cắt mảnh bìa hình tam giác.
Kẻ $2$ đường trung tuyến của tam giác $ABC$, chúng cắt nhau tại $G$.
Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm $G$ thì thấy mảnh bìa thăng bằng.
2. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG PHÂN GIÁC TRONG MỘT TAM GIÁC
Câu hỏi trang 74 Toán 7 tập 2 KNTT
Mỗi tam giác có mấy đường phân giác?
Trả lời:
Từ mỗi đỉnh của tam giác, ta kẻ được $1$ đường phân giác của tam giác nên mỗi tam giác có $3$ đường phân giác.
Hoạt động 3 trang 74 Toán 7 tập 2 KNTT
Cắt một tam giác bằng giấy. Hãy gấp tam giác vừa cắt để được ba đường phân giác của nó. Mở tờ giấy ra, hãy quan sát và cho biết ba nếp gấp đó có cùng đi qua một điểm không (H.9.33).
Trả lời:
Ba nếp gấp đi qua cùng một điểm.
Luyện tập 2 trang 75 Toán 7 tập 2 KNTT
Cho tam giác $ABC$ có hai đường phân giác $AM, BN$ cắt nhau tại điểm $I$. Hỏi $CI$ có là đường phân giác của góc $C$ không?
Trả lời:
Xét tam giác $ABC$ có $2$ đường phân giác của tam giác cắt nhau điểm $I$ nên đường phân giác còn lại của tam giác cũng đi qua điểm $I$ (tính chất đồng quy của 3 đường phân giác).
Vậy $CI$ có là đường phân giác của góc $C$.
Vận dụng 2 trang 75 Toán 7 tập 2 KNTT
Chứng minh rằng trong tam giác đều, điểm cách đều 3 cạnh của tam giác là trọng tâm của tam giác đó.
Trả lời:
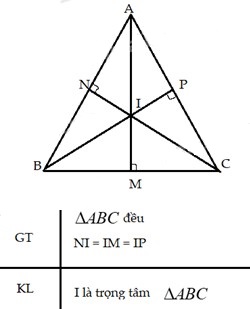
Vì \(\Delta ABC\) đều nên $AB = AC = BC$ (tính chất tam giác đều)
Vì $I$ là điểm cách đều $3$ cạnh của tam giác nên là giao điểm của $3$ đường phân giác của tam giác $ABC$
Áp dụng ví dụ 2, ta được, $AI$ là đường trung tuyến của \(\Delta ABC\)
Tương tự, ta cũng được $BI, CI$ là đường trung tuyến của \(\Delta ABC\)
Vậy $I$ là giao điểm của ba đường đường trung tuyến của \(\Delta ABC\) nên $I$ là trọng tâm của \(\Delta ABC\).
Chú ý: Với tam giác đều, giao điểm của 3 đường trung tuyến cũng là giao điểm của 3 đường phân giác.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 20 21 22 23 24 25 trang 76 sgk Toán 7 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 9.20 trang 76 Toán 7 tập 2 KNTT
Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp vào chỗ chấm hỏi để được các đẳng thức:
$BG = ? BN, CG = ? CP$;
$BG = ? GN, CG = ? GP$.
Bài giải:
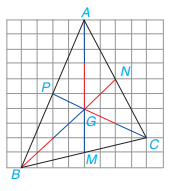
Vì $G$ là trọng tâm của \(\Delta ABC\) nên \(BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP\)
Ta có:
$GN = BN – BG = BN – \dfrac{2}{3}BN = \dfrac{1}{3}BN$;
$GP = CP – CG = CP – \dfrac{2}{3}CP = \dfrac{1}{3}CP$
Do đó, $BN = 3. GN ; CP = 3. GP$
Như vậy, \(BG = \dfrac{2}{3}BN = \dfrac{2}{3}.3.GN = 2GN; CG = \dfrac{2}{3}CP = \dfrac{2}{3}.3.GP = 2GP\)
Vậy:
\(BG = \dfrac{2}{3}BN, CG = \dfrac{2}{3}CP\);
$BG = 2GN; CG = 2GP$.
Giải bài 9.21 trang 76 Toán 7 tập 2 KNTT
Chứng minh rằng:
a) Trong một tam giác cân, hai đường trung tuyến ứng với 2 cạnh bên là hai đoạn thẳng bằng nhau.
b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Bài giải:
a) Ta có hình vẽ sau đây:
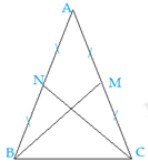
Gọi BM, CN là 2 đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow MA = MC = \dfrac{1}{2}AC\);
$NA = NB = \dfrac{1}{2}AB$
Vì \(\Delta ABC\) cân tại $A$ nên $AB = AC$ (tính chất)
Do đó, $AM = MC = NA = NB$
Xét \(\Delta ANC\) và \(\Delta AMB\), ta có:
• $AN = AM$
• \(\widehat A\) chung
• $AC = AB$
\(\Rightarrow \Delta ANC = \Delta AMB\) (c.g.c)
\(\Rightarrow NC = MB\) (2 cạnh tương ứng)
Vậy 2 đường trung tuyến ứng với 2 cạnh bên của tam giác cân là hai đoạn thẳng bằng nhau.
b) Ta có hình vẽ sau đây:
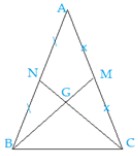
Vì \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G\)
\(\Rightarrow G\) là trọng tâm của tam giác \(ABC\).
\(\Rightarrow GB = \dfrac{2}{3}BM\); \(GC = \dfrac{2}{3}CN\) (tính chất đường trung tuyến trong tam giác)
Mà \(BM = CN\) (giả thiết) nên \(GB = GC\).
Tam giác \(GBC\) có \(GB = GC\) nên \(∆GBC\) cân tại \(G\).
\(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\) (tính chất tam giác cân).
Xét \(∆BCN\) và \(∆CBM\) có:
• \(BC\) là cạnh chung
• \(CN = BM\) (giả thiết)
• \(\widehat{GCB} = \widehat{GBC}\) (chứng minh trên)
Suy ra \(∆BCN = ∆CBM\) (c.g.c)
\(\Rightarrow \widehat{NBC} = \widehat{MCB}\) (hai góc tương ứng).
\(\Rightarrow ∆ABC\) cân tại \(A\) (tam giác có hai góc bằng nhau là tam giác cân)
Giải bài 9.22 trang 76 Toán 7 tập 2 KNTT
Cho tam giác $ABC$ có các đường trung tuyến $BM$ và $CN$ cắt nhau tại $G$. Biết góc $GBC$ lớn hơn góc $GCB$. Hãy so sánh $BM$ và $CN$.
Bài giải:
Ta có hình vẽ sau đây:
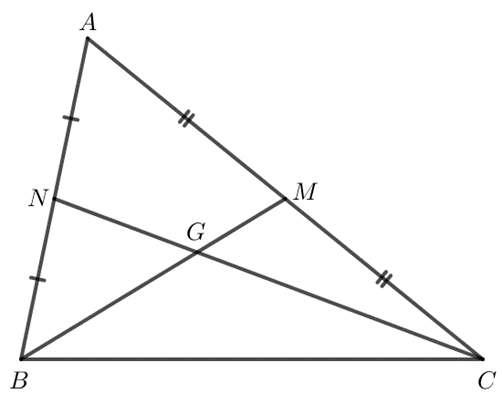
Xét $∆GBC$ có \(\widehat{GBC} > \widehat{GCB}\) nên $GC > GB$.
Do $G$ là trọng tâm của $∆ABC$ nên:
$CG = \dfrac{2}{3}CN, BG = \dfrac{2}{3}BM$.
Khi đó $\dfrac{2}{3}CN > \dfrac{2}{3}BM$.
Do đó $CN > BM$.
Vậy $CN > BM$.
Giải bài 9.23 trang 76 Toán 7 tập 2 KNTT
Kí hiệu $I$ là điểm đồng quy của ba đường phân giác trong tam giác $ABC$. Tính góc $BIC$ khi biết góc $BAC$ bằng $120^\circ $.
Bài giải:
Ta có hình vẽ sau đây:
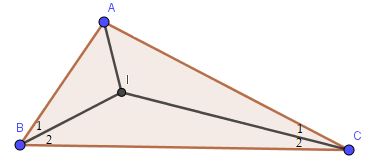
Vì $BI$ là tia phân giác của góc $ABC$ nên:
\(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì $CI$ là tia phân giác của góc $ACB$ nên:
\(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Áp dụng định lí tổng ba góc trong tam giác $ABC$, ta có:
$\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \\ \Rightarrow \widehat {ABC} + \widehat {ACB} = 180^\circ – \widehat {BAC} = 180^\circ – 120^\circ = 60^\circ \\ \Rightarrow \widehat {{B_2}} + \widehat {{C_2}} = \dfrac{1}{2}.\left( {\widehat {ABC} + \widehat {ACB}} \right) = \dfrac{1}{2}.60^\circ = 30^\circ $
Áp dụng định lí tổng ba góc trong tam giác $BIC$, ta có:
$\widehat {BIC} + \widehat {{B_2}} + \widehat {{C_2}} = 180^\circ \\ \Rightarrow \widehat {BIC} = 180^\circ – \left( {\widehat {{B_2}} + \widehat {{C_2}}} \right) = 180^\circ – 30^\circ = 150^\circ $
Vậy \(\widehat {BIC} = 150^\circ \)
Giải bài 9.24 trang 76 Toán 7 tập 2 KNTT
Gọi $BE$ và $CF$ là hai đường phân giác của tam giác $ABC$ cân tại $A$. Chứng minh $BE = CF$.
Bài giải:
Ta có hình vẽ sau đây:
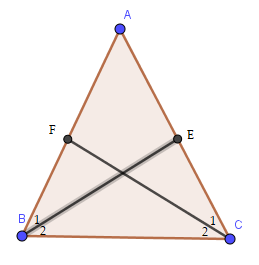
Vì tam giác $ABC$ cân tại $A$ nên:
\(AB = AC; \widehat {ABC} = \widehat {ACB}\) (tính chất)
Vì $BE$ là là tia phân giác của góc $ABC$ nên:
\(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì $CF$ là tia phân giác của góc $ACB$ nên:
\(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Do đó, \(\widehat {{B_1}} = \widehat {{C_1}}\)
Xét \(\Delta ABE\) và \(\Delta ACF\), ta có:
• \(\widehat A\) chung
• $AB = AC$
• \(\widehat {{B_1}} = \widehat {{C_1}}\)
$\Rightarrow \Delta ABE = \Delta ACF $ (g.c.g)
\(\Rightarrow BE = CF\) (2 cạnh tương ứng)
Giải bài 9.25 trang 76 Toán 7 tập 2 KNTT
Trong tam giác $ABC$, hai đường phân giác của các góc $B$ và $C$ cắt nhau tại $D$. Kẻ $DP$ vuông góc với $BC, DQ$ vuông góc với $CA, DR$ vuông góc với $AB$.
a) Hãy giải thích tại sao $DP = DR$.
b) Hãy giải thích tại sao $DP = DQ$.
c) Từ câu a và b suy ra $DR = DQ$. Tại sao $D$ nằm trên tia phân giác của góc $A$? (Đây là một cách chứng minh định lí 2).
Bài giải:
Ta có hình vẽ sau đây:
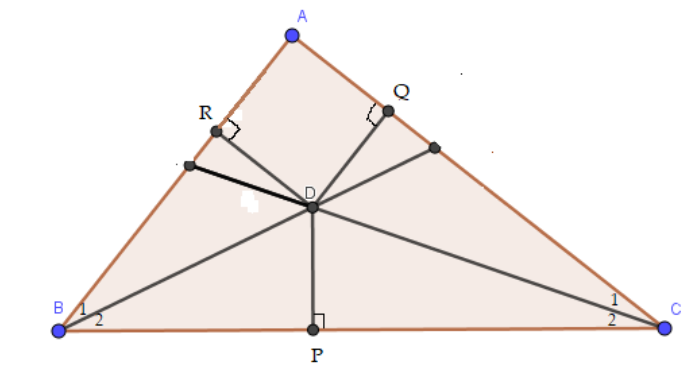
a) Vì $BD$ là tia phân giác của góc $ABC$ nên
\(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì $CD$ là tia phân giác của góc $ACB$ nên
\(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Xét \(\Delta BDP\) vuông tại P và \(\Delta BDR\) vuông tại R, ta có:
• \(\widehat {{B_2}} = \widehat {{B_1}}\)
• $BD$ chung
\(\Rightarrow \Delta BDP = \Delta BDR\) (cạnh huyền – góc nhọn)
\(\Rightarrow DP = DR\) (2 cạnh tương ứng) (1)
b) Xét \(\Delta CDP\) vuông tại P và \(\Delta CDQ\) vuông tại Q, ta có:
• \(\widehat {{C_2}} = \widehat {{C_1}}\)
• $CD$ chung
\(\Rightarrow \Delta CDP = \Delta CDQ\) (cạnh huyền – góc nhọn)
\(\Rightarrow DP = DQ\) (2 cạnh tương ứng) (2)
c) Từ (1) và (2), ta được:
$DR = DQ$ (cùng bằng DP).
⇒ $D$ nằm trên tia phân giác của góc $A$ do $D$ cách đều $AB$ và $AC$.
Bài trước:
👉 Giải bài 14 15 16 17 18 19 trang 71 sgk Toán 7 tập 2 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 26 27 28 29 30 trang 81 sgk Toán 7 tập 2 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 20 21 22 23 24 25 trang 76 sgk Toán 7 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
