Giải bài 21 22 23 24 25 26 trang 18 sgk Toán 6 tập 2 Kết Nối Tri Thức

Nội Dung

Hướng dẫn giải Bài 25. Phép cộng và phép trừ phân số sgk Toán 6 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 21 22 23 24 25 26 trang 18 sgk Toán 6 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 6.

BÀI 25. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN SỐ

Bài toán mở đầu trang 15 Toán 6 tập 2 KNTT

Tuấn ước tính cần 3 giờ ngày chủ nhật để hoàn thành một bức tranh tặng mẹ nhân ngày Quốc tế Phụ nữ 8 – 3. Buổi sáng bạn dành ra $\dfrac{2}{3}$ giờ để vẽ, buổi chiều bạn tiếp tục dành $\dfrac{5}{3}$ giờ để vẽ. Hỏi buổi tối Tuấn cần dành khoảng bao nhiêu giờ nữa để hoàn thành bức tranh.

Trả lời:

Số giờ buổi tối Tuấn cần để hoàn thành bức tranh là:

$3-\dfrac{2}{3}-\dfrac{5}{3}=\dfrac{9}{3}-\dfrac{2}{3}-\dfrac{5}{3}=\dfrac{2}{3}$ (giờ).

1. PHÉP CỘNG HAI PHÂN SỐ

Hoạt động 1 trang 15 Toán 6 tập 2 KNTT

Em hãy nhắc lại quy tắc cộng hai phân số cùng mẫu (có tử và mẫu dương) rồi tính các tổng $\dfrac{8}{{11}} + \dfrac{3}{{11}}$ và $\dfrac{9}{{12}} + \dfrac{{11}}{{12}}$.

Trả lời:

– Quy tắc cộng hai số nguyên cùng mẫu: Ta lấy tử số cộng với nhau và giữ nguyên mẫu số.

– Áp dụng:

$\dfrac{8}{{11}} + \dfrac{3}{{11}} = \dfrac{{8 + 3}}{{11}} = \dfrac{{11}}{{11}} = 1$.

$\dfrac{9}{{12}} + \dfrac{{11}}{{12}} = \dfrac{{9 + 11}}{{12}} = \dfrac{{20}}{{12}}$$ = \dfrac{{20:4}}{{12:4}} = \dfrac{5}{3}$.

Luyện tập 1 trang 16 Toán 6 tập 2 KNTT

Tính:

$\dfrac{{ – 7}}{{12}} + \dfrac{5}{{12}}$; $\dfrac{{ – 8}}{{11}} + \dfrac{{ – 19}}{{11}}$.

Trả lời:

Ta có:

$\dfrac{{ – 7}}{{12}} + \dfrac{5}{{12}} = \dfrac{{ – 7 + 5}}{{12}} = \dfrac{{ – 2}}{{12}} = \dfrac{{ – 1}}{{6}}$;

$\dfrac{{ – 8}}{{11}} + \dfrac{{ – 19}}{{11}} = \dfrac{{ – 8 + \left( { – 19} \right)}}{{11}} = \dfrac{{ – 27}}{{11}}$.

Hoạt động 2 trang 16 Toán 6 tập 2 KNTT

Để thực hiện phép cộng $\dfrac{5}{7} + \dfrac{{ – 3}}{4}$, em hãy làm theo các bước sau:

• Quy đồng mẫu hai phân số $\dfrac{5}{7}$ và $\dfrac{{ – 3}}{4}$.

• Sử dụng quy tắc cộng hai phân số cùng mẫu để tính tổng hai phân số sau khi đã quy đồng.

Trả lời:

Ta có: $\dfrac{5}{7} = \dfrac{{5.4}}{{7.4}} = \dfrac{{20}}{{28}}$ và $\dfrac{{ – 3}}{4} = \dfrac{{ – 3.7}}{{4.7}} = \dfrac{{ – 21}}{{28}}$

Như vậy $\dfrac{{20}}{{28}} + \dfrac{{ – 21}}{{28}} = \dfrac{{20 + \left( { – 21} \right)}}{{28}} = \dfrac{-1}{{28}}$

Luyện tập 2 trang 16 Toán 6 tập 2 KNTT

Tính: $\dfrac{{ – 5}}{8} + \dfrac{{ – 7}}{{20}}$.

Trả lời:

$BCNN(8,20) = 40$

Ta có:

$\dfrac{{ – 5}}{8}+ \dfrac{{ – 7}}{{20}} = \dfrac{{ – 5.5}}{{8.5}} + \dfrac{{ – 7.2}}{{20.2}} \\=\dfrac{{ – 25}}{{40}}+ \dfrac{{ – 14}}{{40}} = \dfrac{{ – 25 + \left( { – 14} \right)}}{{40}} = \dfrac{{ – 39}}{{40}}$.

Hoạt động 3 trang 16 Toán 6 tập 2 KNTT

Tính các tổng $\dfrac{1}{2} + \dfrac{{ – 1}}{2}$; $\dfrac{1}{2} + \dfrac{1}{{ – 2}}$.

Em có nhận xét gì về các kết quả nhận được?

Trả lời:

Ta có:

$\dfrac{1}{2} + \dfrac{{ – 1}}{2} = \dfrac{{1 +(-1)}}{2} = \dfrac{0}{2} = 0\\\dfrac{1}{2} + \dfrac{1}{{ – 2}} = \dfrac{1}{2} + \dfrac{1.(-1)}{{ (- 2).(-1)}} = \dfrac{1}{2} + \dfrac{{ – 1}}{2} =\dfrac{0}{2} = 0$

Nhận xét: Các phép tính trên đều có kết quả bằng 0.

Câu hỏi trang 16 Toán 6 tập 2 KNTT

Trả lời:

Số đối của $0$ là $0$ vì $0 + 0 = 0$.

Luyện tập 3 trang 16 Toán 6 tập 2 KNTT

Tìm số đối của các số sau: $\dfrac{1}{3};\dfrac{{ – 1}}{3}$ và $\dfrac{{ – 4}}{5}$.

Trả lời:

Ta có:

Số đối của $\dfrac{1}{3}$ là $ – \dfrac{1}{3}$ vì $\dfrac{1}{3} + \left( { – \dfrac{1}{3}} \right) = 0$.

Số đối của $\dfrac{{ – 1}}{3}$ là $\dfrac{1}{3}$ vì $\dfrac{1}{3} + \dfrac{{ – 1}}{3} = \dfrac{1}{3} + \left( { – \dfrac{1}{3}} \right) = 0$.

Số đối của $\dfrac{{ – 4}}{5}$ là $\dfrac{4}{5}$ vì $\dfrac{{ – 4}}{5} + \dfrac{4}{5} = \dfrac{{ – 4 + 4}}{5} = 0$.

2. TÍNH CHẤT CỦA PHÉP CỘNG PHÂN SỐ

Luyện tập 4 trang 17 Toán 6 tập 2 KNTT

Tính một cách hợp lí: $B = \dfrac{{ – 1}}{9} + \dfrac{8}{7} + \dfrac{{10}}{9} + \dfrac{{ – 29}}{7}$.

Trả lời:

Ta có thể tính như sau:

$B = \dfrac{{ – 1}}{9} + \dfrac{8}{7} + \dfrac{{10}}{9} + \dfrac{{ – 29}}{7}\\ = \left( {\dfrac{{ – 1}}{9} + \dfrac{{10}}{9}} \right) + \left( {\dfrac{8}{7} + \dfrac{{ – 29}}{7}} \right)\\ = \dfrac{9}{9} + \dfrac{{ – 21}}{7} = 1 – 3 = – 2$.

Vậy $B=-2$.

3. PHÉP TRỪ HAI PHÂN SỐ

Hoạt động 4 trang 17 Toán 6 tập 2 KNTT

Em hãy nhắc lại quy tắc trừ hai phân số cùng mẫu (cả tử và mẫu đều dương) đã học rồi tính các hiệu sau: $\dfrac{7}{{13}} – \dfrac{5}{{13}}$ và $\dfrac{3}{4} – \dfrac{1}{5}$.

Trả lời:

– Quy tắc trừ hai phân số cùng mẫu: Muốn trừ 2 phân số có cùng mẫu số, ta lấy tử số của phân số thứ nhất trừ đi tử số của phân số thứ hai và giữ nguyên mẫu.

– Áp dụng:

$\dfrac{7}{{13}} – \dfrac{5}{{13}} = \dfrac{{7 – 5}}{{13}} = \dfrac{2}{{13}}$

$\dfrac{3}{4} – \dfrac{1}{5} = \dfrac{{15}}{{20}} – \dfrac{4}{{20}} = \dfrac{{15 – 4}}{{20}} = \dfrac{{11}}{{20}}$.

Luyện tập 5 trang 18 Toán 6 tập 2 KNTT

Tính:

a) $\dfrac{3}{5} – \dfrac{{ – 1}}{3}$;

b) $ – 3 – \dfrac{2}{7}$.

Trả lời:

a) Ta có:

$\dfrac{3}{5} – \dfrac{{ – 1}}{3}$ $ = \dfrac{{3.3}}{{5.3}} – \dfrac{{ – 1.5}}{{3.5}}$

$ = \dfrac{9}{{15}} – \dfrac{{ – 5}}{{15}} = \dfrac{{9 – \left( { – 5} \right)}}{{15}} = \dfrac{{14}}{{15}}$

b) Ta có:

$ – 3 – \dfrac{2}{7}$ $= \dfrac{{ – 3.7}}{{1.7}} – \dfrac{2}{7}\\ = \dfrac{{ – 21}}{7} – \dfrac{2}{7}\\ = \dfrac{{ – 21 – 2}}{7}\\ = \dfrac{{ – 23}}{7}$.

Thử thách nhỏ trang 18 Toán 6 tập 2 KNTT

Thay dấu “?” bằng các phân số thích hợp để hoàn thiện sơ đồ dưới đây, biết số trong mỗi ô ở hàng trên bằng tổng của hai số kề nó trong hai ô ở hàng dưới.

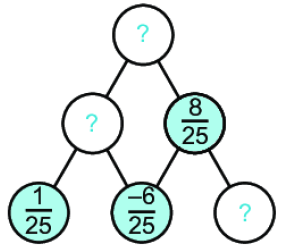
Trả lời:

Từ quy luật: số trong ô ở hàng trên = tổng 2 số trong 2 ô dưới nó ta điền như sau:

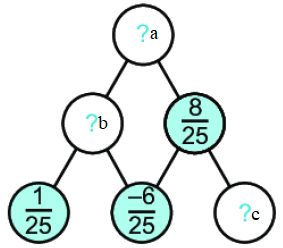
Dấu “?b” ở đây bằng $\dfrac{1}{{25}} + \dfrac{{ – 6}}{{25}} = \dfrac{{1 + \left( { – 6} \right)}}{{25}} = \dfrac{{ – 5}}{{25}} = \dfrac{{ – 1}}{5}$.

Dấu “?c” ở đây bằng $\dfrac{8}{{25}} – \dfrac{{ – 6}}{{25}} = \dfrac{{8 – \left( { – 6} \right)}}{{25}} = \dfrac{{14}}{{25}}$.

Dấu “?a” ở đây bằng $\dfrac{8}{{25}} + \dfrac{{ – 5}}{{25}} = \dfrac{3}{{25}}$.

GIẢI BÀI TẬP

Sau đây là phần Giải bài 21 22 23 24 25 26 trang 18 sgk Toán 6 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 6.21 trang 18 Toán 6 tập 2 KNTT

Tính:

a) $\dfrac{{ – 1}}{{13}} + \dfrac{9}{{13}}$;

b) $\dfrac{{ – 3}}{8} + \dfrac{5}{{12}}$.

Bài giải:

a) Ta có:

$\dfrac{{ – 1}}{{13}} + \dfrac{9}{{13}}$

$ = \dfrac{{ – 1 + 9}}{{13}} = \dfrac{8}{{13}}$

b) Ta có:

$\dfrac{{ – 3}}{8} + \dfrac{5}{{12}}$

$= \dfrac{{ – 3.3}}{{8.3}} + \dfrac{{5.2}}{{12.2}}\\ = \dfrac{{ – 9}}{{24}} + \dfrac{{10}}{{24}} = \dfrac{1}{{24}}$

Giải bài 6.22 trang 18 Toán 6 tập 2 KNTT

Tìm số đối của các phân số sau:

$\dfrac{{ – 3}}{7}; \dfrac{6}{{13}}; \dfrac{4}{{ – 3}}$.

Bài giải:

Ta có:

Số đối của $\dfrac{{ – 3}}{7}$ là $\dfrac{3}{7}$.

Số đối của $\dfrac{6}{{13}}$ là $ – \dfrac{6}{{13}}$.

Số đối của $\dfrac{4}{{ – 3}}$ là $\dfrac{4}{3}$.

Giải bài 6.23 trang 18 Toán 6 tập 2 KNTT

Tính:

a) $\dfrac{{ – 5}}{3} – \dfrac{{ – 7}}{3}$;

b) $\dfrac{5}{6} – \dfrac{8}{9}$.

Bài giải:

a) Ta có:

$\dfrac{{ – 5}}{3} – \dfrac{{ – 7}}{3}$$ = \dfrac{{ – 5 – \left( { – 7} \right)}}{3} =\dfrac{-5+7}{3} = \dfrac{2}{3}$

b) Ta có:

$\dfrac{5}{6} – \dfrac{8}{9}$$ = \dfrac{{5.3}}{{6.3}} – \dfrac{{8.2}}{{9.2}} = \dfrac{{15}}{{18}} – \dfrac{{16}}{{18}}$$ = \dfrac{{15 – 16}}{{18}} = \dfrac{{ – 1}}{{18}}$

Giải bài 6.24 trang 18 Toán 6 tập 2 KNTT

Tính một cách hợp lí:

$A = \left( { – \dfrac{3}{{11}}} \right) + \dfrac{{11}}{8} – \dfrac{3}{8} + \left( { – \dfrac{8}{{11}}} \right)$.

Bài giải:

Ta có thể tính như sau:

$A = \left( { – \dfrac{3}{{11}}} \right) + \dfrac{{11}}{8} – \dfrac{3}{8} + \left( { – \dfrac{8}{{11}}} \right)\\ = \left[ {\left( { – \dfrac{3}{{11}}} \right) + \left( { – \dfrac{8}{{11}}} \right)} \right] + \left( {\dfrac{{11}}{8} – \dfrac{3}{8}} \right)\\ = \dfrac{{ – 11}}{{11}} + \dfrac{8}{8} = – 1 + 1 = 0$

Vậy $A=0$.

Giải bài 6.25 trang 18 Toán 6 tập 2 KNTT

Chị Chi mới đi làm và nhận được tháng lương đầu tiên. Chị quyết định dùng $\dfrac{2}{5}$ số tiền đó để chi tiêu trong tháng, dành $\dfrac{1}{4}$ số tiền để mua quà biếu bố mẹ. Tìm số phần tiền lương còn lại của chị Chi.

Bài giải:

Tổng phần lương đã chi tiêu và mua quà là:

$\dfrac{2}{5} + \dfrac{1}{4} = \dfrac{{2.4}}{{5.4}} + \dfrac{{1.5}}{{4.5}}$$ = \dfrac{8}{{20}} + \dfrac{5}{{20}} = \dfrac{{8 + 5}}{{20}} = \dfrac{{13}}{{20}}$ (số tiền)

Phần tiền lương còn lại của chị Chi là:

$1 – \dfrac{{13}}{{20}} = \dfrac{{20}}{{20}} – \dfrac{{13}}{{20}} = \dfrac{{20 – 13}}{{20}} = \dfrac{7}{{20}}$ (số tiền)

Giải bài 6.26 trang 18 Toán 6 tập 2 KNTT

Mai tự nhẩm tính về thời gian biểu của mình trong một ngày thì thấy $\dfrac{1}{3}$ thời gian là dành cho việc học ở trường; $\dfrac{1}{{24}}$ thời gian là dành cho hoạt động ngoại khóa; $\dfrac{7}{{16}}$ thời gian dành cho hoạt động ăn, ngủ. Còn lại là thời gian cho các công việc cá nhân khác. Hỏi:

a) Mai đã dành bao nhiêu phần thời gian trong ngày cho việc học ở trường và hoạt động ngoại khóa?

b) Mai đã dành bao nhiêu phần thời gian trong ngày cho các công việc cá nhân khác?

Bài giải:

a) Thời gian ở trường và hoạt động ngoại khóa chiếm:

$\dfrac{1}{3} + \dfrac{1}{{24}} = \dfrac{9}{24} = \dfrac{3}{8}$ (thời gian trong ngày)

b) Thời gian Mai dành cho các hoạt động cá nhân khác chiếm:

$1 – \dfrac{{3}}{{8}} – \dfrac{{7}}{{16}} = \dfrac{3}{{16}}$ (thời gian trong ngày).

Bài trước:

👉 Giải bài 14 15 16 17 18 19 20 trang 14 sgk Toán 6 tập 2 Kết Nối Tri Thức

Bài tiếp theo:

👉 Giải bài 27 28 29 30 31 32 33 trang 21 sgk Toán 6 tập 2 Kết Nối Tri Thức

Trên đây là bài Hướng dẫn Giải bài 21 22 23 24 25 26 trang 18 sgk Toán 6 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 6 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“