Nội Dung
Hướng dẫn giải Bài §9. Phân tích đa thức thành nhân tử sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 22 23 24 25 trang 44 sgk Toán 8 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
Bài 9 PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
Bài toán mở đầu trang 42 Toán 8 tập 1 KNTT
Tròn nói: Tớ biết cách tìm được tất cả số $x$ để $2x^2 + x = 0$.
Vuông thắc mắc: Tròn làm như thế nào nhỉ?
Trả lời:
Để tìm x thỏa mãn $2x^2 + x = 0$ thì Tròn cần phân tích đa thức $2x^2 + x$ thành nhân tử.
Ta có: $2x^2 + x = x(2x + 1)$ (phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung).
Khi đó $x(2x + 1) = 0$
⇔ $x = 0$ hoặc $2x + 1 = 0$
⇔ $x = 0$ hoặc $x = \dfrac{{ – 1}}{2}$
Vậy \(x = 0; \,x = \dfrac{{ – 1}}{2}\).
1. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG CÁCH ĐẶT NHÂN TỬ CHUNG
Hoạt động trang 42 Toán 8 tập 1 KNTT
Hãy viết đa thức \({x^2} – 2xy\) thành tích của các đa thức, khác đa thức là số.
Trả lời:
Áp dụng tính chất phân phối giữa phép nhân với phép cộng, ta viết đa thức \({x^2} – 2xy\) thành tích của các đa thức như sau:
\({x^2} – 2xy = x.x – 2xy = x\left( {x – 2y} \right)\).
Luyện tập 1 trang 42 Toán 8 tập 1 KNTT
Phân tích các đa thức sau thành nhân tử:
a) \(6{y^3} + 2y\);
b) \(4\left( {x – y} \right) – 3x\left( {x – y} \right)\).
Trả lời:
a) Ta có:
\(6{y^3} + 2y = 2y.\left( {3{y^2} + 1} \right)\).
b) Ta có:
\(4\left( {x – y} \right) – 3x\left( {x – y} \right) = \left( {x – y} \right)\left( {4 – 3x} \right)\).
Vận dụng 1 trang 42 Toán 8 tập 1 KNTT
Giải bài toán mở đầu bằng cách phân tích \(2{x^2} + x\) thành nhân tử.
Trả lời:
Ta có:
\(2{x^2} + x = 0 \Leftrightarrow x\left( {2x + 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{2x + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = \dfrac{{ – 1}}{2}}\end{array}} \right.\)
Vậy \(x = 0; \,x = \dfrac{{ – 1}}{2}\).
2. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG CÁCH SỬ DỤNG HẰNG ĐẲNG THỨC
Luyện tập 2 trang 43 Toán 8 tập 1 KNTT
Phân tích các đa thức sau thành nhân tử
a) \({\left( {x + 1} \right)^2} – {y^2}\);
b) \({x^3} + 3{x^2} + 3x + 1\);
c) \(8{x^3} – 12{x^2} + 6x – 1\).
Trả lời:
a) Ta có:
\({\left( {x + 1} \right)^2} – {y^2} = \left( {x + 1 + y} \right)\left( {x + 1 – y} \right)\).
b) Ta có:
\({x^3} + 3{x^2} + 3x + 1 = {\left( {x + 1} \right)^3}\).
c) Ta có:
\(8{x^3} – 12{x^2} + 6x – 1 = {\left( {2x} \right)^3} – 3.{\left( {2x} \right)^2}.1 + 3.2x.1 – {1^3} = {\left( {2x – 1} \right)^3}\).
3. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG CÁCH NHÓM CÁC HẠNG TỬ
Luyện tập 3 trang 44 Toán 8 tập 1 KNTT
Phân tích đa thức \(2{x^2} – 4xy + 2y – x\) thành nhân tử.
Trả lời:
Ta có:
\(2{x^2} – 4xy + 2y – x \\= \left( {2{x^2} – 4xy} \right) + \left( {2y – x} \right) \\= 2x\left( {x – 2y} \right) – \left( {x – 2y} \right) \\= \left( {x – 2y} \right)\left( {2x – 1} \right)\).
Vận dụng 2 trang 44 Toán 8 tập 1 KNTT
Tính nhanh giá trị của biểu thức
\(A = {x^2} + 2y – 2x – xy\) tại \(x = 2022,y = 2020\).
Trả lời:
Ta có:
\(A = {x^2} + 2y – 2x – xy \\= \left( {{x^2} – 2x} \right) + \left( {2y – xy} \right) \\= x\left( {x – 2} \right) + y\left( {2 – x} \right) \\= x\left( {x – 2} \right) – y\left( {x – 2} \right) \\= (x-y)(x-2) \).
Thay \(x = 2022,y = 2020\) vào $A$ ta được:
\(A = (2022 – 2020)(2022-2) = 2.2020 = 4040\).
Tranh luận trang 44 Toán 8 tập 1 KNTT
Phân tích đa thức \({x^3} – x\) thành nhân tử.
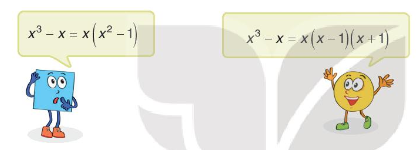
Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.
Trả lời:
Ta có:
\({x^3} – x = x\left( {{x^2} – 1} \right) = x\left( {x – 1} \right)\left( {x + 1} \right)\)
⇒ Bạn Tròn có kết quả đúng, bạn Vuông chưa phân tích triệt để.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 22 23 24 25 trang 44 sgk Toán 8 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 2.22 trang 44 Toán 8 tập 1 KNTT
Phân tích các đa thức sau thành nhân tử:
a) ${x^2} + xy$;
b) $6{a^2}b – 18ab$;
c) ${x^3} – 4x$;
d) ${x^4} – 8x$.
Bài giải:
a) Ta có:
${x^2} + xy = x.x + x.y = x\left( {x + y} \right)$
b) Ta có:
$6{a^2}b – 18ab = 6ab\left( {a – 3} \right)$
c) Ta có:
${x^3} – 4x = x\left( {{x^2} – 4} \right) = x\left( {x – 2} \right)\left( {x + 2} \right)$
d) Ta có:
${x^4} – 8x = x\left( {{x^3} – 8} \right) = x\left( {x – 2} \right)\left( {{x^2} + 2x + 4} \right).$
Giải bài 2.23 trang 44 Toán 8 tập 1 KNTT
Phân tích các đa thức sau thành nhân tử:
a) \({x^2} – 9 + xy + 3y\);
b) \({x^2}y + {x^2} + xy – 1\).
Bài giải:
a) Ta có:
\({x^2} – 9 + xy + 3y \\= \left( {{x^2} – 9} \right) + \left( {xy + 3y} \right) \\= \left( {x – 3} \right)\left( {x + 3} \right) + y\left( {x + 3} \right) \\= \left( {x + 3} \right)\left( {x – 3 + y} \right)\)
b) Ta có:
\({x^2}y + {x^2} + xy – 1 \\= \left( {{x^2}y + xy} \right) + \left( {{x^2} – 1} \right) \\= xy\left( {x + 1} \right) + \left( {x + 1} \right)\left( {x – 1} \right) \\= \left( {x + 1} \right)\left( {xy + x – 1} \right)\)
Giải bài 2.24 trang 44 Toán 8 tập 1 KNTT
Tìm $x$ biết:
a) \({x^2} – 4x = 0\);
b) \(2{x^3} – 2x = 0\).
Bài giải:
a) Ta có:
${x^2} – 4x = 0\\ \Leftrightarrow x\left( {x – 4} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x – 4 = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 4}\end{array}} \right.$
Vậy \(x \in \left\{ {0;4} \right\}\).
b) Ta có:
$2{x^3} – 2x = 0\\ \Leftrightarrow 2x\left( {{x^2} – 1} \right) = 0\\ \Leftrightarrow 2x\left( {x – 1} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x – 1 = 0\\x + 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = – 1\end{array} \right.$
Vậy \(x \in \left\{ {0;1; – 1} \right\}\).
Giải bài 2.25 trang 44 Toán 8 tập 1 KNTT
Một mảnh vườn hình vuông có độ dài cạnh bằng $x$ (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng $y$ (mét) (H.2.2).

a) Viết biểu thức tính diện tích $S$ của đường bao quanh mảnh vườn theo $x$ và $y$.
b) Phân tích $S$ thành nhân tử rồi tính $S$ khi $x=102 m, \,y=2 m$.
Bài giải:
a) Ta có:
\(S = {x^2} – {\left( {x – 2y} \right)^2}\)
Vậy diện tích $S$ của đường bao quanh mảnh vườn là \({x^2} – {\left( {x – 2y} \right)^2} \,(m^2)\).
b) Phân tích đa thức $S$ thành nhân tử, ta được:
\(S = {x^2} – {\left( {x – 2y} \right)^2} \\= \left( {x – x + 2y} \right)\left( {x + x – 2y} \right) \\= 2y.\left( {2x – 2y} \right) = 2y.2\left( {x – y} \right) \\= 4y\left( {x – y} \right)\)
Thay $x=102 m, \,y=2 m$ thì:
\(S = 4.2.\left( {102 – 2} \right) = 800\) (\({m^2}\)).
Bài trước:
👉 Giải bài 16 17 18 19 20 21 trang 41 sgk Toán 8 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 26 27 trang 46 sgk Toán 8 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 22 23 24 25 trang 44 sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
