Nội Dung
Hướng dẫn giải Bài Luyện tập chung trang 86 sgk Toán 7 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 29 30 31 32 trang 86 sgk Toán 7 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
GIẢI BÀI TẬP LUYỆN TẬP CHUNG
Sau đây là phần Giải bài 29 30 31 32 trang 86 sgk Toán 7 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 4.29 trang 86 Toán 7 tập 1 KNTT
Cho Hình 4.73. Hãy tính các độ dài $a, b$ và số đo $x, y$ của các góc trên hình vẽ.
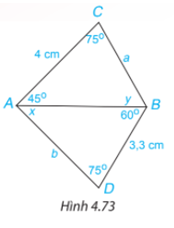
Bài giải:
Xét tam giác ABC có:
$\widehat {BAC} + \widehat {ABC} + \widehat C = {180^o}\\ \Rightarrow {45^o} + y + {75^o} = {180^o}\\ \Rightarrow y = {60^o}$
Xét tam giác ABD có:
$\widehat {DAB} + \widehat {DBA} + \widehat D = {180^o}\\ \Rightarrow x + {60^o} + {75^o} = {180^o}\\ \Rightarrow x = {45^o}$
Xét 2 tam giác ABC và ADB có:
\(\widehat {DAB} = \widehat {CAB} = {45^o}\)
$AB$ chung
\(\widehat D = \widehat C = {75^o}\)
⇒ \(\Delta ABC = \Delta ADB\) (g.c.g)
⇒ BC=BD (2 cạnh tương ứng), mà $BD = 3,3$ cm ⇒ $a= BC= 3,3$cm
AC=AD (2 cạnh tương ứng), mà $AC = 4$ cm ⇒ $b = AD = 4$cm.
Vậy $x = {45^o}; y = {60^o}; a = 3,3 cm; b = 4 cm$.
Giải bài 4.30 trang 86 Toán 7 tập 1 KNTT
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho $OA = OB, OM =ON, OA > OM$.
Chứng minh rằng:
a) \(\Delta OAN = \Delta OBM\);
b) \(\Delta AMN = \Delta BNM\).
Bài giải:
Ta vẽ hình như sau:
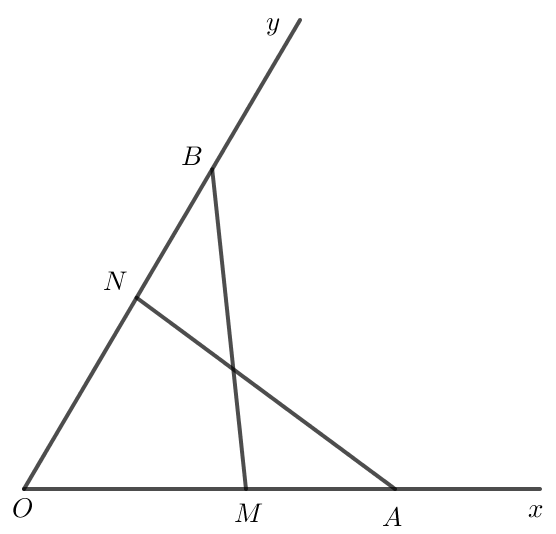
a) Xét tam giác OAN và OBM có:
$OA=OB$
\(\widehat{O}\) chung
$OM=ON$
⇒ \(\Delta OAN = \Delta OBM\) (c.g.c)
b) Do \(\Delta OAN = \Delta OBM\) nên AN=BM (2 cạnh tương ứng);
\(\widehat {OAN} = \widehat {OBM}\) (2 góc tương ứng)
⇒ \(\widehat {NAM} = \widehat {MBN}\)
Do $OA + AM = OM$; $OB + BN = ON$
Mà $OA = OB, OM =ON$
⇒ $AM=BN$
Xét hai tam giác AMN và BNM có:
$AN=BM$
\(\widehat {NAM} = \widehat {MBN}\)
$AM=BN$
⇒ \(\Delta AMN = \Delta BNM\) (c.g.c)
Giải bài 4.31 trang 86 Toán 7 tập 1 KNTT
Cho Hình 4.74, biết $OA = OB, OC = OD$. Chứng minh rằng:
a) $AC = BD$;
b) \(\Delta ACD = \Delta BDC\).
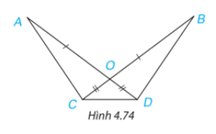
Bài giải:
a) Ta có: $OA = OB, OC = OD$ nên $AD=BC$
Do $OC=OD$ nên tam giác OCD cân ⇒ \(\widehat {OCD} = \widehat {ODC}\)
Xét 2 tam giác ACD và BDC có:
$AD=BC$
\(\widehat {OCD} = \widehat {ODC}\)
$CD$ chung
⇒ \(\Delta ACD = \Delta BCD\) (c.g.c)
⇒ $AC=BD$ (hai cạnh tương ứng)
b) Xét hai tam giác ACD và BDC có:
$AO=BO$
$CO=DO$
$AC=BD$
⇒ \(\Delta ACD = \Delta BDC\) (c.c.c)
Giải bài 4.32 trang 86 Toán 7 tập 1 KNTT
Cho tam giác MBC vuông tại M có \(\widehat B = 60^o\). Gọi A là điểm nằm trên tia đối của tia MB sao cho $MA = MB$. Chứng minh rằng tam giác ABC là tam giác đều.
Bài giải:
Ta vẽ hình như sau:
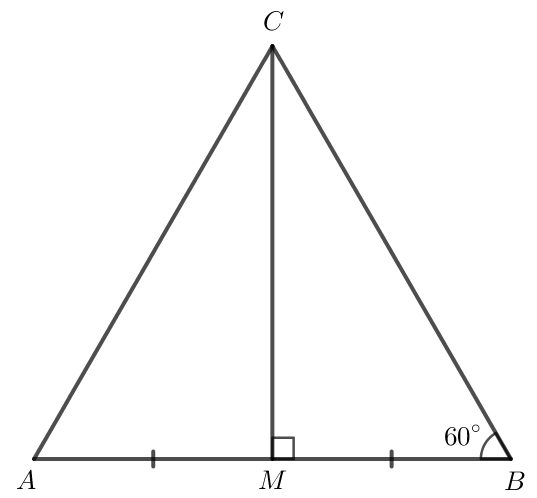
Xét 2 tam giác vuông CMB và CMA có:
$MC$ chung
$MB=MA$
⇒ \(\Delta CMB = \Delta CMA\)(c.g.c)
⇒ $CA = CB$ (2 cạnh tương ứng).
⇒ Tam giác ABC cân tại C.
Mà góc B bằng \(60^o\)
⇒ Tam giác $ABC$ đều.
Bài trước:
👉 Giải bài 23 24 25 26 27 28 trang 84 sgk Toán 7 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 33 34 35 36 37 38 39 trang 87 sgk Toán 7 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 29 30 31 32 trang 86 sgk Toán 7 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
