Nội Dung
Hướng dẫn giải Bài tập cuối chương IV sgk Toán 7 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 33 34 35 36 37 38 39 trang 87 sgk Toán 7 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
GIẢI BÀI TẬP CUỐI CHƯƠNG IV
Sau đây là phần Giải bài 33 34 35 36 37 38 39 trang 87 sgk Toán 7 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 4.33 trang 87 Toán 7 tập 1 KNTT
Tính các số đo $x, y$ trong tam giác dưới đây (H.4.75).
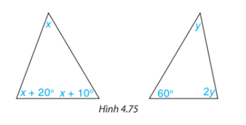
Bài giải:
Áp dụng định lí tổng ba góc trong tam giác
– Ta có:
$x + x + {20^o} + x + {10^o} = {180^o}\\ \Rightarrow 3x = {150^o}\\ \Rightarrow x = {50^o}$
– Ta có:
$y + {60^o} + 2y = {180^o}\\ \Rightarrow 3y = {120^o}\\ \Rightarrow y = {40^o}$
Vậy $x = {50^o}; y = {40^o}$.
Giải bài 4.34 trang 87 Toán 7 tập 1 KNTT
Trong Hình 4.76, có $AM = BM, AN = BN$. Chứng minh rằng \(\widehat {MAN} = \widehat {MBN}\).
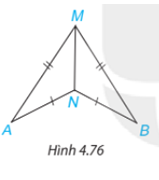
Bài giải:
Xét 2 tam giác MNA và MNB có:
$AM=BM$
$AN=BN$
$MN$ chung
⇒ \(\Delta MNA = \Delta MNB\) (c.c.c)
⇒ \(\widehat {MAN} = \widehat {MBN}\) (2 góc tương ứng)
Giải bài 4.35 trang 87 Toán 7 tập 1 KNTT
Trong Hình 4.77, có $AO = BO$, \(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng $AM = BN$.
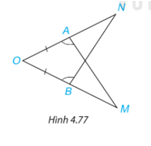
Bài giải:
Xét 2 tam giác OAM và OBN có:
\(\widehat {OAM} = \widehat {OBN}\)
$AO=BO$
Góc $O$ chung
⇒ \(\Delta OAM = \Delta OBN\) (g.c.g)
⇒ $AM=BN$ (2 cạnh tương ứng).
Giải bài 4.36 trang 87 Toán 7 tập 1 KNTT
Trong Hình 4.78, ta có \(AN = BM, \widehat {BAN} = \widehat {ABM}\). Chứng minh rằng \(\widehat {BAM} = \widehat {ABN}\).
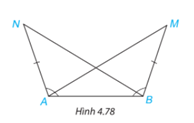
Bài giải:
Xét 2 tam giác ANB và BMA có:
$AN=BM$
\(\widehat {BAN} = \widehat {ABM}\)
$AB$ chung
⇒ \(\Delta ANB = \Delta BMA\) (c.g.c)
⇒ \(\widehat {BAM} = \widehat {ABN}\) (2 góc tương ứng).
Giải bài 4.37 trang 87 Toán 7 tập 1 KNTT
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.
Bài giải:
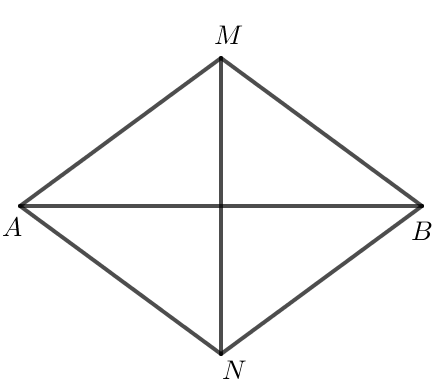
Do M nằm trên đường trung trực của đoạn thẳng AB nên $MA = MB$.
Do N nằm trên đường trung trực của đoạn thẳng AB nên $NA = NB$.
Mà $MA = NA$ (theo giải thiết có $AM = AN$) nên $MA = MB = NA = NB$.
Suy ra $MB = NB$.
Xét tam giác AMB và tam giác ANB có:
$MA = NA$ (giả thiết)
$MB = NB$ (chứng minh trên)
$AB$: cạnh chung
Do đó, ∆AMB = ∆ANB (c.c.c).
Suy ra \(\widehat {AMB} = \widehat {ANB}\) (hai góc tương ứng).
Vậy $MB = NB$ và \(\widehat {AMB} = \widehat {ANB}\).
Giải bài 4.38 trang 87 Toán 7 tập 1 KNTT
Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) \(\Delta BAM = \Delta CAN\);
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Bài giải:
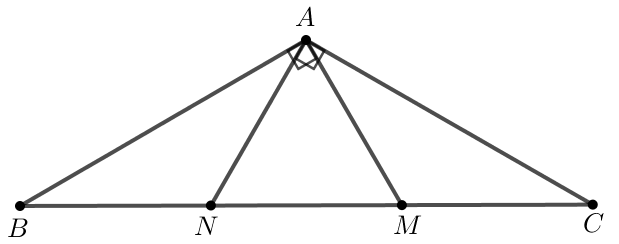
a) Xét 2 tam giác vuông BAM và CAN có:
$AB=AC$ (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
⇒ \(\Delta BAM = \Delta CAN\) (g.c.g)
b) Xét tam giác ABC cân tại A, có:
\(\widehat {A{\rm{ }}} = 120^\circ \)
\(\widehat B = \widehat C = \frac{{{{180}^o} – {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
$\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} – \widehat {AMB} = {180^o} – {60^o} = {120^o}$
Xét tam giác MAC có:
$\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C$
\(\Rightarrow \) Tam giác $AMC$ cân tại $M$.
Vì \(\Delta BAM = \Delta CAN\) ⇒ $BM=CN$ ⇒ $BN=MC$.
Xét 2 tam giác ANB và AMC có:
$AB=AC$
\(AN = AM\) (do \(\Delta BAM = \Delta CAN\))
$BN=MC$
⇒ \(\Delta ANB = \Delta AMC\) (c.c.c)
Mà tam giác AMC cân tại M.
⇒ Tam giác $ANB$ cân tại $N$.
Giải bài 4.39 trang 87 Toán 7 tập 1 KNTT
Cho tam giác ABC vuông tại A có \(\widehat {B} = {60^o}\). Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
Bài giải:
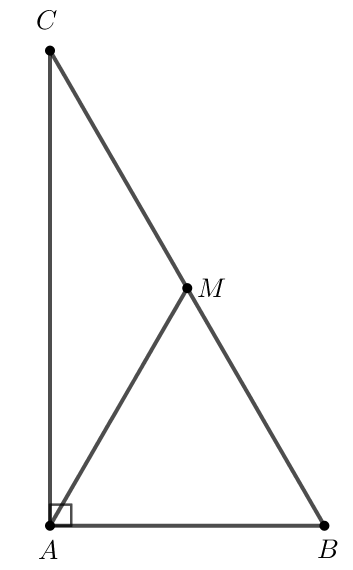
a) Xét tam giác ABC có:
$\widehat A + \widehat B + \widehat C = {180^o}\\ ⇒ {90^o} + {60^o} + \widehat C = {180^o}\\ ⇒ \widehat C = {30^o}$
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
⇒ Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
$\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ ⇒ {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ ⇒ \widehat {CMA} = {120^o}\\ v \widehat {BMA} = {180^o} – \widehat {CMA} = {180^o} – {120^o} = {60^o}$
Xét tam giác ABM có:
$\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ ⇒ {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ ⇒ \widehat {BAM} = {60^o}$
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Do tam giác CAM cân tại M nên $MA = MC$ (1).
Do tam giác BAM là tam giác đều nên $MA = MB$ (2).
Từ (1) và (2) ta có $MB = MC$.
Mà M nằm giữa B và C nên M là trung điểm của BC.
Vậy M là trung điểm của BC.
Bài trước:
👉 Giải bài 29 30 31 32 trang 86 sgk Toán 7 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 trang 92 sgk Toán 7 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 33 34 35 36 37 38 39 trang 87 sgk Toán 7 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
