Giải bài 30 31 32 trang 24 sgk Toán 8 tập 1 Kết Nối Tri Thức

Nội Dung

Hướng dẫn giải Bài §5. Phép chia đa thức cho đơn thức sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 30 31 32 trang 24 sgk Toán 8 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.

Bài 5 PHÉP CHIA ĐA THỨC CHO ĐƠN THỨC

Bài toán mở đầu trang 22 Toán 8 tập 1 KNTT

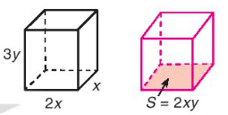
Cho hai khối hộp chữ nhật: khối hộp thứ nhất có ba kích thước $x, 2x$ và $3y$; khối hộp thứ hai có diện tích đáy là $2xy$. Tính chiều cao (cạnh bên) của khối hộp thứ hai, biết rằng hai khối hộp có cùng thể tích.

Trả lời:

Thể tích của khối hộp thứ nhất là:

$2x . x . 3y = 6x^2y$.

Vì hai khối hộp có cùng thể tích nên khối hộp thứ hai có thể tích $6x^2y$.

Chiều cao của khối hộp thứ hai là:

$6x^2y : 2xy = 3x$.

Vậy chiều cao (cạnh bên) của khối hộp thứ hai là 3x.

1. CHIA ĐƠN THỨC CHO ĐƠN THỨC

Hoạt động 1 trang 22 Toán 8 tập 1 KNTT

Hãy nhớ lại cách chia đơn thức cho đơn thức trong trường hợp chúng có một biến và hoàn thành các yêu cầu sau:

a) Thực hiện phép chia $6{x^3}:3{x^2}$.

b) Với $a,b \in \mathbb{R}$ và $b \ne 0;m,n \in \mathbb{N}$, hãy cho biết:

• Khi nào thì $a{x^m}$ chia hết cho $b{x^n}$.

• Nhắc lại cách thực hiện phép chia $a{x^m}$ cho $b{x^n}$.

Trả lời:

a) Ta có:

$6{x^3}:3{x^2} = \left( {6:3} \right).\left( {{x^3}:{x^2}} \right) = 2x$.

b) • Khi $m \ge n$ thì $a{x^m}$ chia hết cho $b{x^n}$.

• Để chia $a{x^m}$ cho $b{x^n}$ ta thực hiện phép chia $a:b$ và ${x^m}:{x^n}$ rồi nhân 2 kết quả với nhau.

Hoạt động 2 trang 23 Toán 8 tập 1 KNTT

Với mỗi trường hợp sau, hãy đoán xem đơn thức $A$ có chia hết cho đơn thức $B$ không; nếu chia hết, hãy tìm thương của phép chia $A$ cho $B$ và giải thích cách làm:

a) $A = 6{x^3}y,B = 3{x^2}y$;

b) $A = {x^2}y,B = x{y^2}$.

Trả lời:

a) Đơn thức $A$ chia hết cho đơn thức $B$:

$A:B = 6{x^3}y:3{x^2}y = \left( {6:3} \right).\left( {{x^3}:{x^2}} \right).\left( {y:y} \right) = 2x$

b) Đơn thức $A$ không chia hết cho đơn thức $B$ vì số mũ của biến $y$ trong $B$ lớn hơn số mũ của biến $y$ trong $A$.

Luyện tập 1 trang 23 Toán 8 tập 1 KNTT

Trong các phép chia sau đây, phép chia nào không là phép chia hết? Tại sao? Tìm thương của các phép chia còn lại:

a) $ – 15{x^2}{y^2}$ chia cho $3{x^2}y$;

b) $6xy$ chia cho $2yz$;

c) $4x{y^3}$ chia cho $6x{y^2}$.

Trả lời:

a) Ta có:

$ – 15{x^2}{y^2}:3{x^2}y = \left( { – 15:3} \right).\left( {{x^2}:{x^2}} \right):\left( {{y^2}:y} \right) = – 5y$

b) Không là phép chia hết vì số mũ của biến $z$ trong $2yz$ lớn hơn số mũ của biến $z$ trong $6xy$.

c) Ta có:

$4x{y^3}:6x{y^2} = \left( {4:6} \right).\left( {x:x} \right).\left( {{y^3}:{y^2}} \right) = \dfrac{2}{3}y$

Vận dụng 1 trang 23 Toán 8 tập 1 KNTT

Giải bài toán mở đầu:

Trả lời:

Chiều cao của khối hộp thứ hai là:

$6{x^2}y:2xy = \left( {6:2} \right).\left( {{x^2}:x} \right).\left( {y:y} \right) = 3x$

Vậy chiều cao (cạnh bên) của khối hộp thứ hai là $3x$.

2. CHIA ĐA THỨC CHO ĐƠN THỨC

Luyện tập 2 trang 24 Toán 8 tập 1 KNTT

Làm tính chia

$\left( {6{x^4}{y^3} – 8{x^3}{y^4} + 3{x^2}{y^2}} \right):2x{y^2}$.

Trả lời:

Ta có:

$\left( {6{x^4}{y^3} – 8{x^3}{y^4} + 3{x^2}{y^2}} \right):2x{y^2}\\ = 6{x^4}{y^3}:2x{y^2} – 8{x^3}{y^4}:2x{y^2} + 3{x^2}{y^2}:2x{y^2}\\ = \left( {6:2} \right).\left( {{x^4}:x} \right).\left( {{y^3}:{y^2}} \right) – \left( {8:2} \right).\left( {{x^3}:x} \right).\left( {{y^4}:{y^2}} \right) + \left( {3:2} \right).\left( {{x^2}:x} \right).\left( {{y^2}:{y^2}} \right)\\ = 3{x^3}y – 4{x^2}{y^2} + \dfrac{3}{2}x.$

Vận dụng 2 trang 24 Toán 8 tập 1 KNTT

Tìm đa thức $A$ sao cho:

$A.\left( { – 3xy} \right) = 9{x^3}y + 3x{y^3} – 6{x^2}{y^2}$.

Trả lời:

Ta có:

$A.\left( { – 3xy} \right) = 9{x^3}y + 3x{y^3} – 6{x^2}{y^2}\\ ⇒ A = \left( {9{x^3}y + 3x{y^3} – 6{x^2}{y^2}} \right):\left( { – 3xy} \right)\\ = 9{x^3}y:\left( { – 3xy} \right) + 3x{y^3}:\left( { – 3xy} \right) – 6{x^2}{y^2}:\left( { – 3xy} \right)\\ = – 3{x^2} – {y^2} + 2xy.$

GIẢI BÀI TẬP

Sau đây là phần Giải bài 30 31 32 trang 24 sgk Toán 8 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1.30 trang 24 Toán 8 tập 1 KNTT

a) Tìm đơn thức $M$ biết rằng $\dfrac{7}{3}{x^3}{y^2}:M = 7x{y^2}$.

b) Tìm đơn thức $N$ biết rằng $N:0,5x{y^2}z = – xy$.

Bài giải:

a) Ta có:

$\dfrac{7}{3}{x^3}{y^2}:M = 7x{y^2}$

$⇒ M = \dfrac{7}{3}{x^3}{y^2}:7x{y^2} = \left( {\dfrac{7}{3}:7} \right).\left( {{x^3}:x} \right).\left( {{y^2}:{y^2}} \right) = \dfrac{1}{3}{x^2}.$

b) Ta có:

$N:0,5x{y^2}z = – xy$

$⇒ N = \left( { – xy} \right).0,5x{y^2}z = \left( { – 0,5} \right).\left( {x.x} \right).\left( {y.{y^2}} \right).z = – 0,5{x^2}{y^3}z.$

Giải bài 1.31 trang 24 Toán 8 tập 1 KNTT

Cho đa thức $A = 9x{y^4} – 12{x^2}{y^3} + 6{x^3}{y^2}$. Với mỗi trường hợp sau đây, xét xem $A$ có chia hết cho đơn thức $B$ hay không? Thực hiện phép chia trong trường hợp $A$ chia hết cho $B$.

a) $B = 3{x^2}y$;

b) $B = – 3x{y^2}$.

Bài giải:

a) Đa thức $A$ không chia hết cho đơn thức $B$ vì hạng tử $ 9x{y^4}$ có số mũ của biến $x$ nhỏ hơn số mũ của biến $x$ trong $B$.

b) Đa thức $A$ có chia hết cho đơn thức $B$:

$A:B = \left( {9x{y^4} – 12{x^2}{y^3} + 6{x^3}{y^2}} \right):\left( { – 3x{y^2}} \right)\\ = 9x{y^4}:\left( { – 3x{y^2}} \right) – 12{x^2}{y^3}:\left( { – 3x{y^2}} \right) + 6{x^3}{y^2}:\left( { – 3x{y^2}} \right)\\ = – 3{y^2} + 4xy – 2{x^2}.$

Giải bài 1.32 trang 24 Toán 8 tập 1 KNTT

Thực hiện phép chia

$\left( {7{y^5}{z^2} – 14{y^4}{z^3} + 2,1{y^3}{z^4}} \right):\left( { – 7{y^3}{z^2}} \right)$.

Bài giải:

Ta có:

$\left( {7{y^5}{z^2} – 14{y^4}{z^3} + 2,1{y^3}{z^4}} \right):\left( { – 7{y^3}{z^2}} \right)\\ = 7{y^5}{z^2}:\left( { – 7{y^3}{z^2}} \right) – 14{y^4}{z^3}:\left( { – 7{y^3}{z^2}} \right) + 2,1{y^3}{z^4}:\left( { – 7{y^3}{z^2}} \right)\\ = – {y^2} + 2yz – 0,3{z^2}.$

Bài trước:

👉 Giải bài 24 25 26 27 28 29 trang 21 sgk Toán 8 tập 1 Kết Nối Tri Thức

Bài tiếp theo:

👉 Giải bài 33 34 35 36 37 38 trang 25 26 sgk Toán 8 tập 1 Kết Nối Tri Thức

Trên đây là bài Hướng dẫn Giải bài 30 31 32 trang 24 sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“