Nội Dung
Hướng dẫn giải Bài §11. Hình thang cân sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 4 5 6 7 8 trang 55 sgk Toán 8 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
Bài 11 HÌNH THANG CÂN
Bài toán mở đầu trang 52 Toán 8 tập 1 KNTT
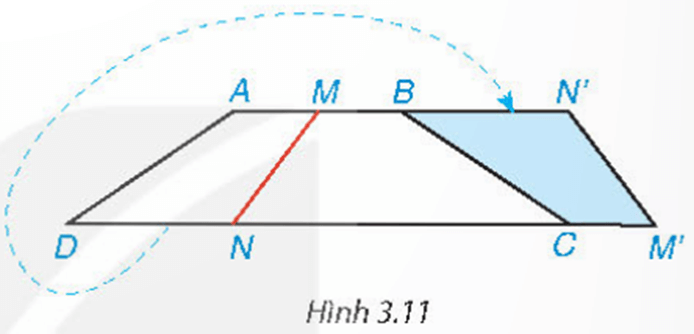
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
Trả lời:
Ta cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy.
Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu nên $\widehat {AMN} = \widehat {M’}$ (1)
Tứ giác $ABCD$ là hình thang cân có $AB // CD$
Mà theo cách ghép thì chỗ ghép ở các đỉnh $M, B$ tạo thành đường thẳng $AN’$, chỗ ghép ở các đỉnh $N, C$ tạo thành đường thẳng $DM’$. Do đó $AN’ // M’D$.
Suy ra $\widehat {AMN} = \widehat {MNM’}$ (so le trong) (2)
Từ (1) và (2) suy ra $\widehat {MNM’} = \widehat {M’}$
Xét tứ giác $MN’M’N$ có $MN’ // M’N$ nên là hình thang.
Lại có $\widehat {MNM’} = \widehat {M’}$ nên $MN’M’N$ là hình thang cân.
1. HÌNH THANG. HÌNH THANG CÂN
Luyện tập 1 trang 53 Toán 8 tập 1 KNTT
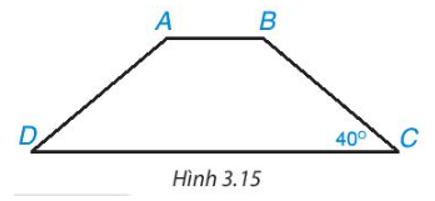
Tính các góc của hình thang cân$ ABCD (AB // CD)$, biết \(\widehat C = {40^o}\) (H.3.15).
Trả lời:
Hình thang cân $ABCD (AB //CD)$ nên ta có:
\(\widehat A = \widehat B; \,\widehat C = \widehat D = {40^o}\)
Mà \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Khi đó: \(\widehat A + \widehat A + {40^o} + {40^o} = {360^o}\)
Hay: \(2\widehat A + {80^o} = {360^o}\)
Suy ra: \(2\widehat A = {360^o} – {80^o} = {280^o}\)
Do đó: \(\widehat A = {140^o}\) nên \(\widehat B = {140^o}\)
Vậy: \(\widehat A = {140^o}; \,\widehat B = {140^o}; \,\widehat C = {40^o}; \,\widehat D = {40^o}\).
2. TÍNH CHẤT CỦA HÌNH THANG CÂN
Hoạt động 1 trang 53 Toán 8 tập 1 KNTT
Cho hình thang cân $ABCD, AC // CD$ và $AB < CD$ (H.3.16).

a) Từ $A$ và $B$ kẻ $AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD$. Chứng minh rằng $AH = BI$ bằng cách chứng minh $∆AHI = ∆IBA$.
b) Chứng minh $∆AHD = ∆BIC$, từ đó suy ra $AD = BC$.
Trả lời:
a) Vì $ABCD$ là hình thang cân ($AB // CD$) nên \(\widehat {BAI} = \widehat {AIH}\) (hai góc so le trong).
Ta có $AH ⊥ DC, BI ⊥ DC$ suy ra $AH // BI$.
Do đó \(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Xét $∆AHI$ và $∆IBA$ có:
\(\widehat {BAI} = \widehat {AIH}\) (chứng minh trên);
Cạnh $AI$ chung;
\(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Do đó $∆AHI = ∆IBA$ (c.g.c).
Suy ra $AH = BI$ (hai cạnh tương ứng).
b) Vì $ABCD$ là hình thang cân ($AC // CD$) nên \(\widehat C = \widehat D\).
Mặt khác: $∆AHD$ và $∆BIC$ có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) và \(\widehat C = \widehat D\) nên:
\(90^o – \widehat C = 90^o – \widehat {BIC} \Leftrightarrow \widehat {DAH} = \widehat {CBI}\)
Xét $∆AHD$ và $∆BIC$ có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) (vì $AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD$);
\(AH = BI\) (chứng minh trên)
\(\widehat {DAH} = \widehat {CBI}\) (chứng minh trên).
Do đó $∆AHD = ∆BIC$ (g.c.g).
Suy ra $AD = BC$ (hai cạnh tương ứng).
Luyện tập 2 trang 53 Toán 8 tập 1 KNTT
Cho tứ giác $ABCD$ như Hình 3.18. Biết rằng \(\widehat A = \widehat B = \widehat {{D_1}}\). Chứng minh rằng $AD = BC$.

Trả lời:
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên $AB // CD$.
Suy ra tứ giác $ABCD$ là hình thang.
Mặt khác hình thang $ABCD$ có \(\widehat A = \widehat B\) nên $ABCD$ là hình thang cân.
Do đó $AD = BC$ (đpcm).
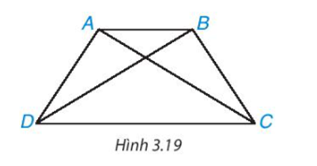
Hoạt động 2 trang 54 Toán 8 tập 1 KNTT
Cho hình thang cân $ABCD$, kẻ hai đường chéo $AC, BD$ (H.3.19). Hãy chứng minh $∆ACD = ∆BDC$. Từ đó suy ra $AC = BD$.
Trả lời:
Vì $ABCD$ là hình thang cân ($AC // CD$) nên:
$AD = BC; \,\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}$
Xét $∆ACD$ và $∆BDC$ có:
$AD = BC$ (chứng minh trên);
\(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\) (chứng minh trên);
Cạnh $CD$ chung.
Do đó $∆ACD = ∆BDC$ (c.g.c)
Suy ra $AC = BD$ (hai góc tương ứng).
Luyện tập 3 trang 54 Toán 8 tập 1 KNTT
Cho tam giác $ABC$ cân tại $A$. Kẻ một đường thẳng $d$ song song với $BC, d$ cắt cạnh $AB$ tại $D$ và cắt cạnh $AC$ tại $E$ (H.3.20).

a) Tứ giác $DECB$ là hình gì?
b) Chứng minh $BE = CD$.
Trả lời:
a) Theo đề bài: $d // BC$ nên $DE // BC$
Suy ra $DECB$ là hình thang.
Vì tam giác $ABC$ cân tại $A$ nên \(\widehat B = \widehat C\).
Hình thang $DECB$ có \(\widehat B = \widehat C\) nên tứ giác $DECB$ là hình thang cân.
b) Hình thang cân $DECB$ có $BE$ và $CD$ là hai đường chéo.
Do đó $BE = CD$ (đpcm).
3. DẤU HIỆU NHẬN BIẾT
Thực hành trang 55 Toán 8 tập 1 KNTT
a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:
– Vẽ hai đường thẳng song song $a, b$. Trên $a$ lấy hai điểm $A, B$.
– Vẽ hai cung tròn tâm $A$ và $B$ có cùng bán kính sao cho cung tròn tâm $A$ cắt $b$ tại $C$; cung tròn tâm $B$ cắt $b$ tại $D$ và hai đoạn thẳng $AC, BD$ cắt nhau. Hình thang $ABCD$ có hai đường chéo $AC$ và $BD$ bằng nhau.

b) Hình thang $ABCD$ có là hình thang cân không? Vì sao?
Trả lời:
a) Học sinh vẽ hình theo các bước đã nêu ở đề bài.
b) Hình thang $ABCD$ có hai đường chéo $AC = BD$.
Do đó $ABCD$ là hình thang cân.
Vận dụng trang 55 Toán 8 tập 1 KNTT
Hãy giải bài toán mở đầu.
Trả lời:
Ta cắt một mảnh giấy hình thang cân $ABCD$ bằng một nhát thẳng cắt cả hai cạnh đáy.
Lật hình thang $AMND$ rồi ghép với hình thang $MBCN$ dọc theo các cạnh bên của hình thang ban đầu, khi đó ta được một hình mới.
Tứ giác $ABCD$ là hình thang cân nên $AB // CD$ suy ra $MN’ // M’N$.
Do đó $MN’M’N$ là hình thang.
Vì $AB // CD$ nên \(\widehat {AMN} = \widehat {MNC}\) (2 góc so le trong)
Mà \(\widehat {AMN} = \widehat {CM’N’}\) (theo giả thiết)
\(⇒ \widehat {MNC} = \widehat {CM’N}\)
Mà hai góc này là hai góc kề một đáy nên suy ra $MN’M’N$ là hình thang cân.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 4 5 6 7 8 trang 55 sgk Toán 8 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 3.4 trang 55 Toán 8 tập 1 KNTT
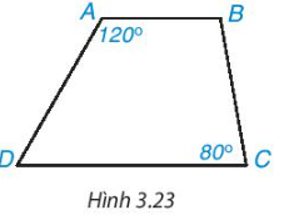
Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao?
Bài giải:
Để hình thang $ABCD$ là hình thang cân thì:
\(\widehat A = \widehat B = {120^o}; \,\widehat C = \widehat D = {80^o}\).
Suy ra:
\(\widehat A + \widehat B + \widehat C + \widehat D=120^o+120^o+80^o+80^o=400^o>360^o\) (không thỏa mãn định lí tổng bốn góc trong một tứ giác).
Khi đó, $ABCD$ không phải là tứ giác.
Do đó $ABCD$ cũng không phải là hình thang cân.
Giải bài 3.5 trang 55 Toán 8 tập 1 KNTT
Cho hình thang $ABCD$ ($AB // CD$). Kẻ đường thẳng vuông góc với $AC$ tại $C$ và đường thẳng vuông góc với $BD$ tại $D$, hai đường thẳng này cắt nhau tại $E$. Chứng minh rằng nếu $EC = ED$ thì hình thang $ABCD$ là hình thang cân.
Bài giải:
Gọi $O$ là giao điểm của $AC$ và $BD$.

Xét $∆DOE$ và $∆COE$ có:
\(\widehat {O{\rm{D}}E} = \widehat {OC{\rm{E}}} = {90^o}\) (vì OD ⊥ DE; OC ⊥ CE)
$EC = ED$ (giả thiết)
Cạnh $OE$ chung
Do đó $∆DOE = ∆COE$ (cạnh huyền – cạnh góc vuông).
Suy ra $OC = OD$ (hai cạnh tương ứng).
Do đó tam giác $OCD$ cân tại $O$ nên \(\widehat {{C_1}} = \widehat {{D_1}}\)
Vì $ABCD$ là hình thang nên $AB // CD$ Suy ra:
\(\widehat {{A_1}} = \widehat {{C_1}}; \,\widehat {{B_1}} = \widehat {{D_1}}\) (cặp góc so le trong).
Do đó \(\widehat {{A_1}} = \widehat {{B_1}}\) (vì \(\widehat {{C_1}} = \widehat {{D_1}}\))
Suy ra tam giác $OAB$ cân tại $O$ nên $OA = OB$.
Do $OA = OB, \,OC = OD$ nên $OA + OC = OB + OD$ nên $AC = BD$
⇒ $ABCD$ là hình thang cân theo dấu hiệu nhận biết “nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân”.
Giải bài 3.6 trang 55 Toán 8 tập 1 KNTT
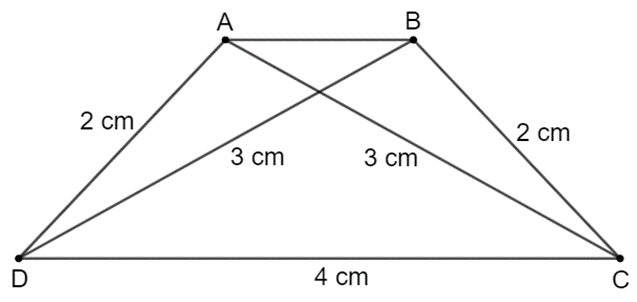
Vẽ hình thang cân $ABCD (AB // CD)$ biết đáy lớn $CD$ dài $4 cm$, cạnh bên dài $2 cm$ và đường chéo dài $3 cm$.
Bài giải:
Cách vẽ hình thang cân $ABCD$ có đáy lớn $CD$ dài $4 cm$, cạnh bên dài $2 cm$ và đường chéo dài $3 cm$:
– Vẽ cạnh $CD = 4 cm$.
– Dùng compa vẽ hai đường tròn $(D; 2 cm)$ và $(C; 3 cm)$. Hai đường tròn này cắt nhau tại điểm $A$.
– Dùng compa vẽ hai đường tròn $(C; 3 cm)$ và $(D; 2 cm)$. Hai đường tròn này cắt nhau tại điểm $B$.
– Nối $AB, AD, BC$ ta được hình thang $ABCD$ (như hình vẽ).
Giải bài 3.7 trang 55 Toán 8 tập 1 KNTT
Hai tia phân giác của hai góc $A, B$ của hình thang cân $ABCD (AB // CD)$ cắt nhau tại điểm $E$ trên cạnh đáy $CD$. Chứng minh rằng $EC = ED$.
Bài giải:
Ta có hình vẽ minh họa sau:

Vì $ABCD$ là hình thang cân nên:
\(\widehat {DAB} = \widehat {ABC};\widehat C = \widehat D;A{\rm{D}} = BC\)
Theo đề bài, ta có $AE, BE$ lần lượt là tia phân giác của \(\widehat {BA{\rm{D}}}\) và \(\widehat {ABC}\)
Suy ra \(\widehat {{A_1}} = \widehat {{A_2}}; \,\widehat {{B_1}} = \widehat {{B_2}}\)
Mà \(\widehat {DAB} = \widehat {ABC}\) nên:
\(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}}\)
Xét $∆ADE$ và $∆BCE$ có:
\(\widehat {{A_2}} = \widehat {{B_2}}\) (chứng minh trên)
$AD = BC$ (chứng minh trên)
\(\widehat {{D}} = \widehat {{C}}\) (chứng minh trên)
Do đó $∆ADE = ∆BCE$ (g.c.g).
Suy ra $EC = ED$ (hai cạnh tương ứng).
Giải bài 3.8 trang 55 Toán 8 tập 1 KNTT
Hình thang cân $ABCD (AB // CD, AB < CD)$ có các đường thẳng $AD, BC$ cắt nhau tại $I$, các đường thẳng $AC, BD$ cắt nhau tại $J$. Chứng minh rằng đường thẳng $IJ$ là đường trung trực của đoạn thẳng $AB$.
Bài giải:
Ta có hình vẽ minh họa sau:
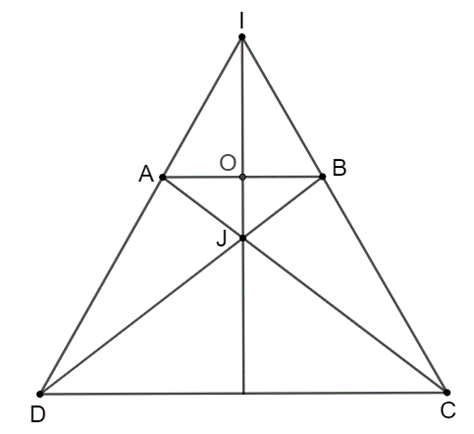
Gọi $O$ là giao điểm của $AB$ và $IJ$.
Vì $ABCD$ là hình thang cân nên:
\(\widehat {BA{\rm{D}}} = \widehat {ABC}; \,\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}; \, AD = BC, \,AC = BD\)
Tam giác $ICD$ cân tại $I$ (vì \(\widehat {ADC} = \widehat {BCD}\)) nên $IC = ID$.
Xét tam giác $ABD$ và $BAC$ có:
$AB$ chung
$AD = BC$ (cmt)
$AC = BD$ (cmt)
Suy ra $∆ABD = ∆BAC$ (c.c.c)
⇒ \(\widehat {A{\rm{D}}B} = \widehat {BC{\rm{A}}}\)
Vì \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}; \,\widehat {A{\rm{D}}B} = \widehat {BC{\rm{A}}}\) nên \(\widehat {J{\rm{D}}C} = \widehat {JC{\rm{D}}}\)
Tam giác $JCD$ cân tại $J$ (vì \(\widehat {J{\rm{D}}C} = \widehat {JC{\rm{D}}}\) ) nên $JC = JD$.
Xét $∆IJD$ và $∆IJC$ có:
$IC = ID$ (chứng minh trên);
\(\widehat {A{\rm{D}}B} = \widehat {BC{\rm{A}}}\);
$JC = JD$ (chứng minh trên).
Do đó $∆IJD = ∆IJC$ (c.g.c).
Suy ra \(\widehat {D{\rm{IJ}}} = \widehat {C{\rm{IJ}}}\) (hai góc tương ứng).
Ta có $ID = IC, \,AD = BC$.
Mà $ID = AI + AD$; $IC = IB + BC$ nên $IA = IB$.
Tam giác $IAB$ cân tại $I$ (vì $IA = IB$) có $IO$ là tia phân giác \(\widehat {AIB}\)
Suy ra $IO$ là đường trung trực của đoạn thẳng $AB$.
Vậy đường thẳng $IJ$ là đường trung trực của đoạn thẳng $AB$.
Bài trước:
👉 Giải bài 1 2 3 trang 51 sgk Toán 8 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 9 10 11 12 trang 56 sgk Toán 8 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 4 5 6 7 8 trang 55 sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
