Nội Dung
Hướng dẫn giải Bài 6. Số vô tỉ. Căn bậc hai số học sgk Toán 7 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 6 7 8 9 10 11 12 trang 32 sgk Toán 7 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
BÀI 6. SỐ VÔ TỈ. CĂN BẬC HAI SỐ HỌC
Bài toán mở đầu trang 29 Toán 7 tập 1 KNTT
Hình tròn: Tớ ghép được một hình vuông có diện tích bằng 2 dm2.
Hình vuông: Không biết số nào biểu thị độ dài cạnh của hình vuông đó nhỉ?
Trả lời:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Độ dài cạnh của hình vuông đó là $\sqrt{2}$ dm (khái niệm căn bậc hai số học).
Vậy độ dài cạnh của hình vuông đó là $\sqrt{2}$ dm.
1. SỐ VÔ TỈ
Hoạt động 1 trang 29 Toán 7 tập 1 KNTT
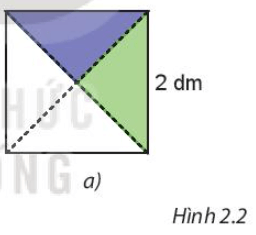
Cắt một hình vuông cạnh bằng 2 dm, rồi cắt nó thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông (H.2.2.a)
Trả lời:
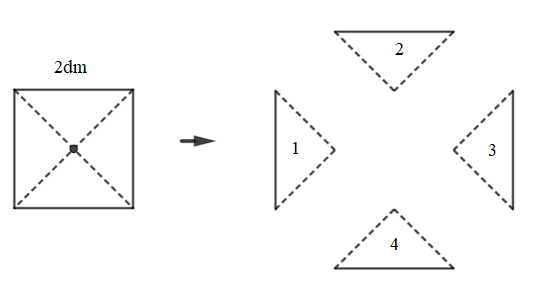
– Bước 1: Cắt một hình vuông cạnh bằng 2 dm.
– Bước 2: Cắt hình vuông thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông.
Hoạt động 2 trang 29 Toán 7 tập 1 KNTT
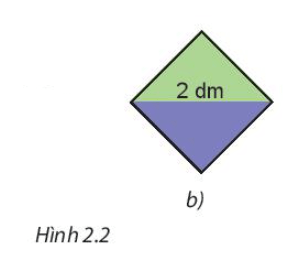
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2.b). Em hãy tính diện tích hình vuông nhận được.
Trả lời:
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông.
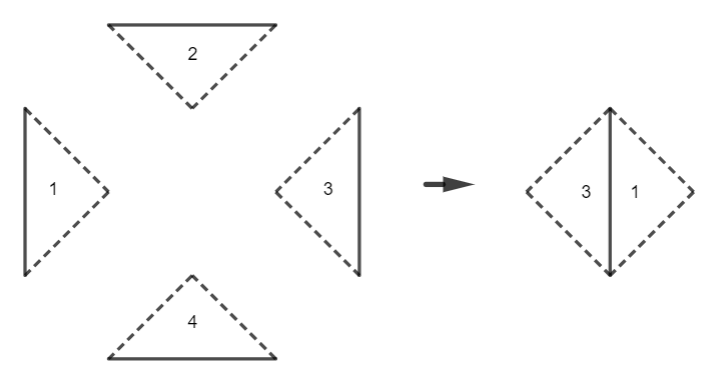
Vì 2 tam giác vuông chiếm một nửa hình vuông ban đầu nên diện tích hình vuông thu được là:
$2.2:2= 2$ (dm2)
Hoạt động 3 trang 29 Toán 7 tập 1 KNTT
Dùng thước có vạch chia để đo độ dài cạnh hình vuông nhận được trong HĐ2. Độ dài cạnh hình vuông này bằng bao nhiêu đềximét ?
Trả lời:
Dùng thước đo ta được cạnh hình vuông dài khoảng $14 cm$.
Ta có: $14 cm = 1,4 dm$.
Vận dụng 1 trang 30 Toán 7 tập 1 KNTT
Người xưa đã tính đường kính thân cây theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, tức là lấy chu vi thân cây chia làm 8 phần bằng nhau (quân bát); bớt đi ba phần (phát tam) còn lại 5 phần (tổn ngũ) rồi chia đôi kết quả (quân nhị). Hãy cho biết người xưa đã ước lượng số \(\pi \) bằng bao nhiêu?
Trả lời:
Theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, có:
\(d = \frac{C}{8}.5:2 = \frac{C}{8}.5.\frac{1}{2} = \frac{{5C}}{{16}} = \frac{C}{{\frac{{16}}{5}}}\)
Theo công thức, có: \(d = \frac{C}{\pi }\)
Như vậy, người xưa đã ước lượng số \(\pi \) bằng \(\frac{{16}}{5} = 3,2\).
2. CĂN BẬC HAI SỐ HỌC
Luyện tập 1 trang 30 Toán 7 tập 1 KNTT
Tính: \(a)\sqrt {16}; b) \sqrt {81} ; c) \sqrt {{{2021}^2}} \).
Trả lời:
a) Vì \({4^2} = 16\) nên \(\sqrt {16} = 4\)
b) Vì \({9^2} = 81\) nên \(\sqrt {81} = 9\)
c) Vì 2021 > 0 nên \(\sqrt {{{2021}^2}} = 2021\).
Vận dụng 2 trang 30 Toán 7 tập 1 KNTT
Sàn thi đấu bộ môn cử tạ có dạng một hình vuông, diện tích 144 m2. Em hãy tính chu vi của sàn thi đấu đó
Trả lời:
Cạnh của sàn thi đấu là: \(\sqrt {144} = 12\) (m)
Chu vi của sàn thi đấu là: $4. 12 = 48$ (m)
Vậy chu vi của sàn thi đấu đó là $48$ m.
3. TÍNH CĂN BẬC HAI SỐ HỌC BẰNG MÁY TÍNH CẦM TAY
Luyện tập 2 trang 31 Toán 7 tập 1 KNTT
Sử dụng máy tính cầm tay tính các căn bậc hai số học sau (làm tròn kết quả với độ chính xác 0,005, nếu cần).
\(a) \sqrt {15} ; b) \sqrt {2,56} ;c) \sqrt {17256} ;d) \sqrt {793881} \)
Trả lời:
Độ chính xác 0,005 tức là ta cần làm tròn đến hàng phần trăm.
a) Ấn các phím:
Ta được kết quả là 3,872983346…
Làm tròn kết quả với độ chính xác 0,005 được $\sqrt {15} \approx 3,87$
b) Ấn các phím:
![]()
Ta được kết quả là $\sqrt {2,56} = 1,6$
c) Ấn các phím:
![]()
Ta được kết quả là 131,362095…
Làm tròn kết quả với độ chính xác 0,005 được $\sqrt {17256} \approx 131,36$
d) Ấn các phím:

Ta được kết quả là $\sqrt {793881} = 891$
Vận dụng 3 trang 31 Toán 7 tập 1 KNTT
Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thế giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 m2.
(Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).
Trả lời:
Độ dài cạnh đáy của kim tự tháp này là:
\(\sqrt {52198,16} \approx 228,469\) (m)
Làm tròn đến chữ số thập phân thứ nhất, ta được: $228,5$ m.
Vậy độ dài cạnh đáy của kim tự tháp này xấp xỉ $228,5$ m.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 6 7 8 9 10 11 12 trang 32 sgk Toán 7 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 2.6 trang 32 Toán 7 tập 1 KNTT
Cho biết \({153^2} = 23409\). Hãy tính \(\sqrt {23409} \)
Bài giải:
Do 1532 = 23409 và 153 > 0 nên \(\sqrt {23409} = 153\).
Giải bài 2.7 trang 32 Toán 7 tập 1 KNTT
Từ các số là bình phương của 12 số tự nhiên đầu tiên, em hãy tìm căn bậc hai số học của các số sau:
a) 9; b) 16; c) 81; d) 121
Bài giải:
a) Vì \({3^2} = 9\) nên \(\sqrt 9 = 3\)
b) Vì \({4^2} = 16\) nên \(\sqrt {16} = 4\)
c) Vì \({9^2} = 81\) nên \(\sqrt {81} = 9\)
d) Vì \({11^2} = 121\) nên \(\sqrt {121} = 11\)
Giải bài 2.8 trang 32 Toán 7 tập 1 KNTT
Khi tìm căn bậc hai số học của một số tự nhiên ta thường phân tích số đó ra thừa số nguyên tố. Chẳng hạn:
Vì \(324 = {2^2}{.3^4} = {({2.3^2})^2} = {18^2}\) nên \(\sqrt {324} = 18\)
Tính căn bậc hai số học của 129 600.
Bài giải:
Ta có:
\(129{\rm{ }}600 = {2^6}{.3^4}{.5^2} = {({2^3}{.3^2}.5)^2} = {360^2}\)
Nên \(\sqrt {129600} = 360\).
Giải bài 2.9 trang 32 Toán 7 tập 1 KNTT
Tính độ dài các cạnh của hình vuông có diện tích bằng:
a) 81 dm2; b) 3 600 m2; c) 1 ha.
Bài giải:
a) Độ dài các cạnh của hình vuông là: \(\sqrt {81} = 9\) (dm)
b) Độ dài các cạnh của hình vuông là: \(\sqrt {3600} = 60\) (m)
c) Đổi 1 ha = 10 000 m2
Độ dài các cạnh của hình vuông là: \(\sqrt {10000} = 100\) (m)
Chú ý: Câu c cần đổi đơn vị trước khi tìm căn bậc hai số học.
Giải bài 2.10 trang 32 Toán 7 tập 1 KNTT
Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn các kết quả với độ chính xác 0,005.
a) 3; b) 41; c) 2 021.
Bài giải:
Làm tròn các kết quả với độ chính xác 0,005 tức là làm tròn đến hàng phần trăm.
a) Ấn các phím:
![]()
Ta được kết quả là 1,732050808.
Làm tròn kết quả với độ chính xác 0,005 được $\sqrt 3 \approx 1,73$
b) Ấn các phím:
![]()
Ta được kết quả là 6,403124237.
Làm tròn kết quả với độ chính xác 0,005 được $\sqrt {41} \approx 6,4$
c) Ấn các phím:
![]()
Ta được kết quả là 44,95553359.
Làm tròn kết quả với độ chính xác 0,005 được $\sqrt {2021} \approx 44,96$.
Giải bài 2.11 trang 32 Toán 7 tập 1 KNTT
Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 8 dm và chiều rộng là 5 dm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu đềximét (làm tròn kết quả đến hàng phần mười)?
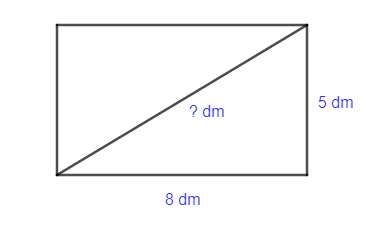
Bài giải:
Ta có: Bình phương độ dài đường chéo của một hình chữ nhật là:
\({5^2} + {8^2} = 25 + 64 = 89\) (dm)
Độ dài đường chéo của một hình chữ nhật là:
\(\sqrt {89} = 9,43398…\)(dm)
Làm tròn kết quả này đến hàng phần mười, ta được: $9,4$ dm.
Vậy độ dài đường chéo của hình chữ nhật đó xấp xỉ $9,4$ dm.
Chú ý: Độ dài đường chéo của một hình chữ nhật bằng căn bậc hai số học của tổng các bình phương độ dài hai cạnh của nó.
Giải bài 2.12 trang 32 Toán 7 tập 1 KNTT
Để lát một mảnh sân hình vuông có diện tích 100 m2, người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50 cm (coi các mạch ghép là không đáng kể)?
Bài giải:
Diện tích một viên gạch là:
502 = 2500 (cm2) = 0,25 m2.
Người ta cần số viên gạch là:
$100 : 0,25 = 400$ (viên).
Vậy người ta cần dùng $400$ viên gạch để lát sân.
Bài trước:
👉 Giải bài 1 2 3 4 5 trang 28 sgk Toán 7 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 13 14 15 16 17 18 trang 36 sgk Toán 7 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 6 7 8 9 10 11 12 trang 32 sgk Toán 7 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
