Nội Dung
Hướng dẫn giải Bài tập cuối chương 3 sgk Toán 8 tập 1 bộ Chân Trời Sáng Tạo. Nội dung bài bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
GIẢI BÀI TẬP CUỐI CHƯƠNG 3
Sau đây là phần Giải Bài tập cuối chương 3 trang 88 89 sgk Toán 8 tập 1 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
CÂU HỎI TRẮC NGHIỆM
Giải bài 1 trang 88 Toán 8 tập 1 CTST
Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó có 2 đoạn tre dài $60cm$ và $80cm$ để làm hai đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều, Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là:
A. $5 m$.
B. $1 m$.
C. $1,5 m$.
D. $2 m$.
Trả lời:
Ta có hình vẽ minh họa sau:
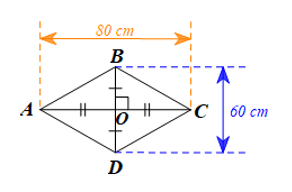
Giả sử hình thoi \(ABCD\) có hai đường chéo \(AC = 80 cm\); \(BD = 60 cm\).
Suy ra:
\(BD \bot AC\) hay \(\widehat {BOA} = 90^\circ \)
\(OA = OC = \frac{1}{2}AC = \frac{1}{2}.80 = 40 cm\)
\(OB = OD = \frac{1}{2}BD = \frac{1}{2}.60 = 30 cm\)
Áp dụng định lý Pythagore vào tam giác vuông \(BOA\) nên ta có:
\(A{B^2} = O{B^2} + O{A^2} = {30^2} + {40^2} = 900 + 1600 = 2500 = {50^2}\)
\(AB = 50 (cm)\)
Chu vi hình thoi là:
\(50.4 = 200 \,(cm) = 2 \,(m)\)
Tổng độ dài bốn đoạn tre dùng làm cạnh của cái diều là $2 m$
⇒ Đáp án: D.
Giải bài 2 trang 88 Toán 8 tập 1 CTST
Cho hình thang cân \(ABCD\) (\(AB // CD\)) có \(\widehat A = 65^\circ \). Số đo góc \(C\) là:
A. \(115^\circ \).
B. \(95^\circ \).
C. \(65^\circ \).
D. \(125^\circ \).
Trả lời:
Ta có hình vẽ minh họa sau:
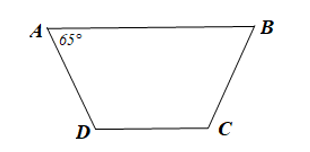
Vì \(ABCD\) là hình thang cân nên \(\widehat C = \widehat D\)
Vì \(AB\) // \(CD\) nên \(\widehat A + \widehat D = 180^\circ \)
Suy ra \(\widehat D = 180^\circ – \widehat A = 180^\circ – 65^\circ = 115^\circ \)
Vậy \(\widehat C = 115^\circ \)
⇒ Đáp án: A.
Giải bài 3 trang 88 Toán 8 tập 1 CTST
Trong các khẳng định sau, khẳng định nào sai?
A. Tứ giác có ba góc vuông là hình chữ nhật.
B. Hình bình hành có một góc vông là hình chữ nhật.
C. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.
D. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
Trả lời:
Theo tính chất hình bình hành: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Đây là tính chất đã có sẵn của hình bình hành, nên khẳng định C là sai.
⇒ Đáp án: C.
Giải bài 4 trang 88 Toán 8 tập 1 CTST
Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Biết \(AB = 8 cm\); \(AC = 15 cm\). Độ dài đoạn \(AM\) là:
A. $8,5 cm$.
B. $8 cm$.
C. $7 cm$.
D. $7,5 cm$.
Trả lời:
Ta có hình vẽ minh họa sau:
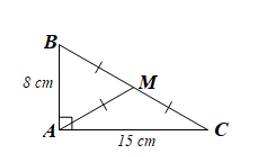
Áp dụng định lí Pythagpre vào \(\Delta ABC\) vuông tại \(A\) ta có:
\(B{C^2} = A{B^2} + A{C^2} = {8^2} + {15^2} = 64 + 225 = 289 = {17^2}\)
\(⇒ BC = 17 cm\)
Xét \(\Delta ABC\) có \(AM\) là trung tuyến nên bằng nửa cạnh huyền \(BC\)
Suy ra \(AM = \frac{1}{2}BC = \frac{1}{2}.17 = 8.5 cm\)
⇒ Đáp án: B.
Giải bài 5 trang 88 Toán 8 tập 1 CTST
Cho hình thoi \(ABCD\) có cạnh bằng \(13 cm \), độ dài đường chéo \(AC\) là $10 cm$. Độ dài đường chéo \(BD\) là:
A. $24 cm$.
B. $12 cm$.
C. $16 cm$.
D. $20 cm$.
Trả lời:
Ta có hình vẽ minh họa sau:
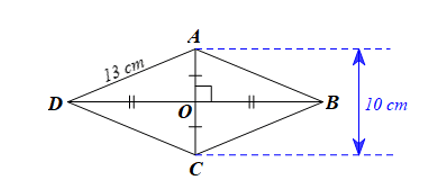
Gọi \(O\) là giao điểm của hai đường chéo
Vì \(ABCD\) là hình thoi (gt) nên:
\(AC\) vuông góc với \(BD\);
\(OB = OD = \frac{1}{2}BD\);
\(OA = OC = \frac{1}{2}AC = \frac{1}{2}.10 = 5 (cm)\)
Áp dụng ĐL Pythagore vào tam giác vuông \(OAB\) ta có:
\(O{A^2} = A{B^2} – O{B^2} = {13^2} – {5^2} = 169 – 25 = 144 = {12^2}\)
\(⇒ OA = 12 cm\)
Suy ra \(AC = 2OA = 2.12 = 24 cm\)
⇒ Đáp án: A.
Giải bài 6 trang 88 Toán 8 tập 1 CTST
Trong các khẳng định sau, khẳng định nào đúng?
A. Hình chữ nhật có hai đường chép bằng nhau là hình vuông.
B. Hình thoi có hai đường chéo vuông góc là hình vuông.
C. Hình thoi có một góc vuông là hình vuông.
D. Hình chữ nhật có một góc vuông là hình vuông.
Trả lời:
Theo tính chất của hình chữ nhật: Hình chữ nhật có hai đường chéo bằng nhau và có bốn góc vuông. Do đó đây là các tính chất đã có sẵn của hình chữ nhật nên A và D là khẳng định sai.
Theo tính chất của hình thoi: Hình thoi có hai đường chéo vuông góc với nhau. Do đó đây là tính chất đã có sẵn của hình thoi nên B là khẳng định sai.
Hình thoi có một góc vuông là hình vuông. Đây là khẳng định đúng.
⇒ Đáp án: C.
Giải bài 7 trang 88 Toán 8 tập 1 CTST
Cho tứ giác \(ABCD\), biết \(\widehat A = 60^\circ ;\;\widehat B = 110^\circ ;\;\widehat D = 70^\circ \). Khi đó số đo góc \(C\) là:
A. \(120^\circ \).
B. \(110^\circ \).
C. \(130^\circ \).
D. \(80^\circ \).
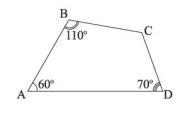
Trả lời:
Xét tứ giác \(ABCD\) ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
\(⇔ \widehat C = 360^\circ – \left( {\widehat A + \widehat B + \widehat D} \right)\)
\(⇔ \widehat C = 360^\circ – \left( {60^\circ + 110^\circ + 70^\circ } \right) = 120^\circ \)
⇒ Đáp án: A.
BÀI TẬP TỰ LUẬN
Giải bài 8 trang 89 Toán 8 tập 1 CTST
Cho hình bình hành \(ABCD\). Các điểm \(E\), \(F\) thuộc đường chéo \(AC\) sao cho \(AE = EF = FC\). Gọi \(M\) là trung điểm của \(BF\) và \(CD\), \(N\) là giao điểm của \(DE\) và \(AB\). Chứng minh rằng:
a) \(M\), \(N\) theo thứ tự là trung điểm của \(CD\), \(AB\);
b) \(EMFN\) là hình bình hành.
Bài giải:
Ta có hình vẽ minh họa sau:
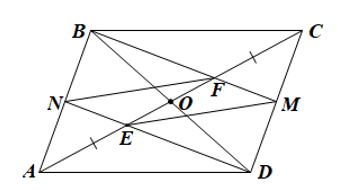
a) Ta có:
\(AE = EF = FC\) nên \(AE = EF = FC = \frac{1}{3}AC\) (1)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) hay \(OA = OC = \frac{1}{2}AC\) và \(AC = 2OA = 2OC\) (2)
Từ (1) và (2) suy ra \(AE = EF = FC = \frac{2}{3}OA = \frac{2}{3}OC\).
Xét \(\Delta BCD\) có \(CO\) là trung tuyến và \(CF = \frac{2}{3}CO\) (cmt)
Suy ra \(F\) là trọng tâm của \(\Delta BCD\)
Suy ra \(BM\) là đường trung tuyến của \(\Delta BCD\)
Suy ra \(M\) là trung điểm của \(CD\)
Xét \(\Delta ABD\) có \(AO\) là trung tuyến và \(AE = \frac{2}{3}AO\) (cmt)
Suy ra \(E\) là trọng tâm của \(\Delta ABD\)
Suy ra \(DN\) là đường trung tuyến của \(\Delta ABD\)
Suy ra \(N\) là trung điểm của \(AB\).
b) Do $M$ là trung điểm của $CD$ (câu a) nên \(MC = MD = \frac{1}{2}CD\).
$N$ là trung điểm của $AB$ (câu a) nên \(NB = NA = \frac{1}{2}AB\).
Mà $AB = CD$ và $AB // CD$ (do $ABCD$ là hình bình hành)
Suy ra $NB = MD$ và $NB // MD$.
Xét tứ giác $BMDN$ có $NB = MD$ và $NB // MD$
Do đó $BMDN$ là hình bình hành.
Suy ra $BM // DN$ và $BM = DN$.
Ta có:
$E$ là trọng tâm của \(\Delta ABD\) nên \(EN = \frac{1}{3}DN\).
$F$ là trọng tâm của \(\Delta BCD\) nên \(FM = \frac{1}{3}BM\).
Mà $DN = BM$ (chứng minh trên) nên $EN = FM$.
Xét tứ giác $EMFN$ có $EN = FM$ và $EN // FM$ (do $BM // DN$)
Suy ra $EMFN$ là hình bình hành.
Giải bài 9 trang 89 Toán 8 tập 1 CTST
Cho tam giác \(ABC\) cân tại \(A\). Gọi \(H\), \(D\) lần lượt là trung điểm của các cạnh \(BC\) và \(AB\).
a) Chứng minh rằng tứ giác \(ADHC\) là hình thang;
b) Gọi \(E\) là điểm đối xứng với \(H\) qua \(D\). Chứng minh rằng tứ giác \(AHBE\) là hình chữ nhật;
c) Tia \(CD\) cắt \(AH\) tại \(M\) và cắt \(BE\) tại \(N\). Chứng minh rằng tứ giác \(AMBN\) là hình bình hành.
Bài giải:
Ta có hình vẽ minh họa sau:
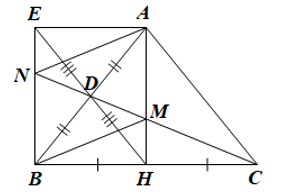
a) Vì \(\Delta ABC\) cân tại \(A\) nên \(\widehat {ABC} = \widehat {ACB}\) và \(AB = AC\)
Vì \(\Delta ABC\) cân tại \(A\), có \(AH\) là trung tuyến (gt)
Suy ra \(AH\) là đường cao
Suy ra \(AH \bot BC\)
Suy ra \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)
Xét \(\Delta AHB\) vuông tại \(H\) ta có: \(HD\) là trung tuyến
Suy ra \(HD = \frac{1}{2}AB\)
Mà \(DA = DB = \frac{1}{2}AB\) (do \(D\) là trung điểm \(AB\))
Suy ra \(DA = DB = HD\)
Suy ra \(\Delta DHB\) cân tại \(D\)
Suy ra \(\widehat {ABC} = \widehat {DHB}\)
Mà \(\widehat {ABC} = \widehat {ACB}\) (cmt)
Suy ra \(\widehat {DHB} = \widehat {ACB}\)
Mà hai góc ở vị trí đồng vị
Suy ra \(DH\) // \(AC\)
Suy ra \(ADHC\) là hình thang.
b) Vì \(E\) đối xứng với \(H\) qua \(D\) (gt)
Suy ra \(D\) là trung điểm của \(HE\)
Xét tứ giác \(AHBE\) ta có:
Hai đường chéo \(HE\) và \(AB\) cắt nhau tại trung điểm \(D\)
Suy ra \(AHBE\) là hình bình hành
Mà \(\widehat {AHB} = 90^\circ \) (cmt)
Suy ra \(AHBE\) là hình chữ nhật.
c) Vì \(AHBE\) là hình chữ nhật (cmt)
Suy ra \(AH // BE\) và \(AH = BE\)
Xét \(\Delta DEN\) và \(\Delta DHM\) ta có:
\(\widehat {NED} = \widehat {DHM}\) (do \(BE // AH\))
\(DE = DH\) (do \(D\) là trung điểm của \(HE\))
\(\widehat {EDN} = \widehat {MDH}\) (đối đỉnh)
Suy ra \(\Delta DEN = \Delta DHM\) (g.c.g)
Suy ra \(EN = MH\) (hai cạnh tương ứng)
Mà \(BE = AH\) (cmt)
Suy ra \(BE – EN = AH – MH\)
Suy ra \(NB = AM\)
Mà \(NB // AM\) (do \(EB // AH\))
Suy ra \(AMBN\) là hình bình hành.
Giải bài 10 trang 89 Toán 8 tập 1 CTST
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Gọi \(M\), \(N\), \(E\) lần lượt là trung điểm của \(AB\), \(AC\), \(BC\).
a) Chứng minh rằng tứ giác \(ANEB\) là hình thang vuông;
b) Chứng minh rằng tứ giác \(ANEM\) là hình chữ nhật;
c) Qua \(M\) kẻ đường thẳng song song với \(BN\) cắt \(EN\) tại \(F\). Chứng minh rằng tứ giác \(AFCE\) là hình thoi;
d) Gọi \(D\) là điểm đối cứng của \(E\) qua \(M\). Chứng minh rằng \(A\) là trung điểm của \(DF\).
Bài giải:
Ta có hình vẽ minh họa sau:
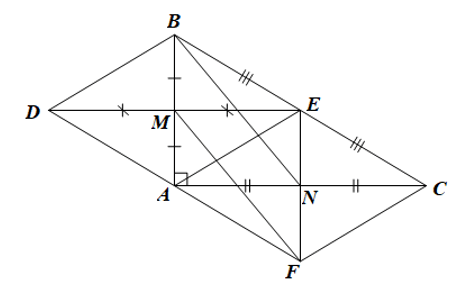
a) Xét tam giác $ABC$ vuông tại $A$ có $E$ là trung điểm của $BC$ nên $AE$ là đường trung tuyến ứng với cạnh huyền của tam giác $ABC$
$⇒ AE = BE = EC = \frac{1}{2}BC$
Vì $AE = EC$ nên $E$ thuộc đường trung trực của $AC$. Vì $N$ là trung điểm của $AC$ nên $N$ thuộc đường trung trực của $AC$.
⇒ EN là đường trung trực của $AC$ hay \(EN \bot AC\)
Ta có \(AB \bot AC, EN \bot AC ⇒ AB // EN\) nên $ANEB$ là hình thang
Vì \(\widehat {BAN} = 90^0\) nên $ANEB$ là hình thang vuông.
b) Ta có: \(M\), \(E\) lần lượt là trung điểm của \(AB\) và \(BC\) (gt);
Suy ra \(ME\) là đường trung bình của \(\Delta ABC\)
Suy ra \(ME // AC\) hay \(ME // AN\)
Mà \(AM // NE\) (do \(AB // NE\))
Suy ra tứ giác \(AMEN\) là hình bình hành
Mà \(\widehat {MAN} = 90^\circ \) nên \(AMEN\) là hình chữ nhật.
c) Xét tứ giác \(BMFN\) có:
\(MF // BN\) (gt) và \(BM // FN\) (do \(AB // NE\))
Suy ra \(BMFN\) là hình bình hành
Suy ra \(BM = FN\)
Mặt khác \(NE = AM\) (tứ giác \(ANEM\) là hình chữ nhật) và \(AM = BM\)
Suy ra \(FN = NE\)
Tứ giác \(AFCE\) có \(N\) là trung điểm của \(AC\) và \(EF\)
Suy ra \(AFCE\) là hình bình hành
Mà \(AC \bot EF\)
Do đó \(AFCE\) là hình thoi.
d) Xét tứ giác \(ADBE\) ta có: \(DE\) và \(AB\) cắt nhau tại \(M\) (gt)
Mà \(M\) là trung điểm của \(AB\) (gt)
\(M\) là trung điểm của \(DE\) (do \(D\) đối xứng với \(E\) qua \(M\))
Suy ra \(ADBE\) là hình bình hành
Suy ra \(AD // BE\) hay \(AD // EC\)
Mà \(AF // EC\) (do \(AECF\) là hình thoi)
Suy ra \(A,D,F\) thẳng hàng (1)
Mà \(ADBE\) là hình bình hành
Suy ra \(BE // AD\)
Mà \(AF = EC\) (do \(AFCE\) là hình thoi); \(EB = EC\) (gt)
Suy ra \(AD = AF\) (2)
Từ (1) và (2) suy ra \(A\) là trung điểm của \(DF\).
Giải bài 11 trang 89 Toán 8 tập 1 CTST
Cho hình bình hành \(ABCD\) có \(AB = 2AD\). Gọi \(E\) và \(F\) lần lượt là trung điểm của \(DF\) và \(CD\), \(I\) là giao điểm của \(AF\) và \(DE\), \(K\) là giao điểm của \(BF\) và \(CE\).
a) Chứng minh rằng tứ giác \(AECF\) là hình bình hành;
b) Tứ giác \(AEFD\) là hình gì? Vì sao?
c) Chứng minh tứ giác \(EIFK\) là hình chữ nhật;
d) Tìm điều kiện của hình bình hành \(ABCD\) để tứ giác \(EIFK\) là hình vuông.
Bài giải:
Ta có hình vẽ minh họa sau:
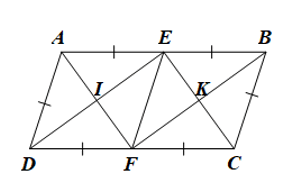
a) Ta có:
\(AE = EB = \frac{1}{2}AB\) (do \(E\) là trung điểm của \(AB\))
\(DF = FC = \frac{1}{2}CD\) (\(F\) là trung điểm của \(CD\))
\(AB = CD\) (do \(ABCD\) là hình bình hành)
Suy ra \(AE = CF = EB = DF\)
Xét tứ giác \(AECF\) ta có:
\(AE // CF\) (do \(AB // CD\))
\(AE = CF\)
Suy ra \(AECF\) là hình bình hành.
b) Vì \(AB = 2AD\) (gt) và \(AB = 2AE\) (do \(E\) là trung điểm của \(AB\))
Suy ra \(AD = AE\)
Xét tứ giác \(AEFD\) có \(AE // DF\) và \(AE = DF\) (cmt)
Suy ra \(AEFD\) là hình bình hành
Mà \(AE = AD\) (cmt)
Suy ra \(AEFD\) là hình thoi.
c) Ta có:
\(AF \bot DE\) (do \(AEFD\) là hình thoi)
và \(AF // EC\) (\(AECF\) là hình bình hành)
Suy ra \(EC \bot DE\)
Suy ra \(\widehat {IEK} = 90^\circ \)
Vì \(AEFD\) là hình thoi nên \(EF = AE\)
Và \(AE = \frac{1}{2}AB\) (gt)
Suy ra \(EF = \frac{1}{2}AB\)
Xét \(\Delta AFB\) có \(FE\) là đường trung tuyến và \(EF = \frac{1}{2}AB\)
Suy ra \(\Delta AFB\) vuông tại \(F\)
Suy ra \(\widehat {IFK} = 90\)
Xét tứ giác \(EIFK\) ta có:
\(\widehat {EIF} = 90\) (do \(AF \bot DE\))
\(\widehat {IEK} = 90^\circ \) (cmt)
\(\widehat {IFK} = 90^\circ \) (cmt)
Suy ra \(EIFK\) là hình chữ nhật.
d) Ta có:
\(EIFK\) là hình vuông, suy ra \(FI = EI\)
Mà \(EI = ID = \frac{1}{2}DE\) (do \(AEFD\) là hình thoi)
\(FI = IA = \frac{1}{2}AF\) (do \(AEFD\) là hình thoi)
Suy ra \(AF = DE\)
Mà \(AEFD\) là hình thoi
Suy ra \(AEFD\) là hình chữ nhật
Suy ra \(\widehat {ADC} = 90^\circ \)
Mà \(ABCD\) là hình bình hành (gt)
Suy ra \(ABCD\) là hình chữ nhật.
Vậy nếu hình bình hành \(ABCD\) là hình chữ nhật thì \(EIFK\) là hình vuông.
Giải bài 12 trang 89 Toán 8 tập 1 CTST
Cho hình hình hành \(ABCD\) có \(AD = 2AB\). Từ \(C\) vẽ \(CE\) vuông góc với \(AB\) tại \(E\). Nối \(E\) với trung điểm \(M\) của \(AD\). Từ \(M\) vẽ \(MF\) vuông góc với \(CE\) tại \(F\), \(MF\) cắt \(BC\) tại \(N\).
a) Tứ giác \(MNCD\) là hình gì?
b) Chứng minh tam giác \(EMC\) cân tại \(M\);
c) Chứng minh rằng \(\widehat {BAD} = 2\widehat {AEM}\).
Hướng dẫn:
a) Chứng minh \(EN = NC = NB = \) \(\frac{1}{2}BC\).
b) Chứng minh \(\widehat {AEM} = \widehat {EMN} = \widehat {NMC} = \widehat {MCD} = \frac{1}{2}\widehat {NCD}\).
Bài giải:
Ta có hình vẽ minh họa sau:
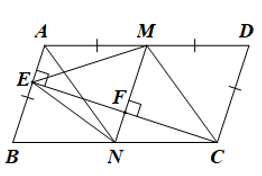
a) Ta có:
\(MN \bot CE\) (gt)
\(AB \bot CE\) (gt)
Suy ra \(MN // AB\)
Mà \(AB // CD\) (do \(ABCD\) là hình bình hành) nên \(MN // CD\)
Xét tứ giác \(MNCD\) ta có:
\(MN // CD\) (cmt)
\(MD // CN\) (do \(AD // BC\))
Suy ra \(MNCD\) là hình bình hành
Lại có:
\(AD = 2AB\) (gt);
\(AD = 2MD\) (do \(M\) là trung điểm của \(AD\))
\(AB = CD\) (do \(ABCD\) là hình bình hành)
Suy ra \(MD = CD\)
Hình bình hành \(MNCD\) có \(MD = CD\) (cmt) nên là hình thoi.
b) Vì \(MNCD\) là hình thoi nên:
\(MD = CD = NC = MN = \frac{1}{2}AD = \frac{1}{2}BC\) (do \(AD = BD\))
Do \(NC = \frac{1}{2}BC\) nên \(N\) là trung điểm của \(BC\)
Xét \(\Delta EBC\) vuông tại \(E\) có \(EN\) là trung tuyến nên \(EN = \frac{1}{2}BC\)
Suy ra \(EN = NB = NC = \frac{1}{2}BC\)
Suy ra \(\Delta NEC\) cân tại \(N\)
Mà \(NF\) là đường cao (do \(MF \bot EC\))
Suy ra \(NF\) cũng là trung tuyến, phân giác, trung trực của \(\Delta NEC\)
Suy ra \(F\) là trung điểm \(EC\)
Xét \(\Delta MEC\) có \(MF\) là đường cao đồng thời là trung tuyến
Suy ra \(\Delta EMC\) cân tại \(M\).
c) Vì \(AB\) // \(MN\) (cmt)
Suy ra \(\widehat {AEM} = \widehat {EMN}\) (so le trong)
Mà \(\widehat {EMN} = \widehat {NMC}\) (do \(MF\) là phân giác)
\(\widehat {NMC} = \widehat {MCD}\) (do \(MN // CD\))
Suy ra \(\widehat {AEM} = \widehat {MCD}\)
Mà \(\widehat {MCD} = \frac{1}{2}\widehat {BCD}\) (do \(MNCD\) là hình thoi)
Và \(\widehat {BCD} = \widehat {BAD}\) (do \(ABCD\) là hình bình hành)
Suy ra \(\widehat {AEM} = \frac{1}{2}\widehat {BAD}\)
Suy ra \(\widehat {BAD} = 2\widehat {AEM}\).
Bài trước:
👉 Giải bài 1 2 3 4 5 trang 87 sgk Toán 8 tập 1 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 trang 96 97 sgk Toán 8 tập 1 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải Bài tập cuối chương 3 trang 88 89 sgk Toán 8 tập 1 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
