Nội Dung
Hướng dẫn giải Giải Bài tập cuối chương 9 sgk Toán 6 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ câu trả lời các câu hỏi, bài giải các bài tập, giúp các bạn học sinh học tốt môn toán 6.
GIẢI BÀI TẬP CUỐI CHƯƠNG 9
Giải bài 1 trang 107 Toán 6 tập 2 CTST
Hãy liệt kê tất cả các kết quả có thể xảy ra của mỗi phép thử nghiệm sau:
a) Lấy ra 1 quả bóng từ hộp có 10 quả bóng được đánh số từ 1 đến 10.
b) Bạn Lan chọn một ngày trong tháng 8 để đi về quê.
Bài giải:
a) Các kết quả có thể xảy ra là: bóng được đánh số 1,2,3,4,5,6,7,8,9,10
b) Bạn Lan chọn một ngày trong tháng 8 để đi về quê, kết quả có thể xảy ra là bất kì ngày nào trong tháng (từ ngày 1/8 đến 31/8).
Giải bài 2 trang 107 Toán 6 tập 2 CTST
Trong hộp có 1 cây bút xanh, 1 cây bút đỏ, 1 cây bút tím. Hãy liệt kê các kết quả có thể xảy ra của mỗi hoạt động sau:
a) Lấy ra 1 cây bút từ hộp.
b) Lấy ra cùng một lúc 2 cây bút từ hộp.
Bài giải:
a) Lấy ra 1 cây bút từ hộp, kết quả có thể xảy ra là: bút xanh, bút đỏ hoặc bút tím
b) Lấy ra cùng 1 lúc 2 cây bút từ hộp, có 3 kết quả có thể xảy ra: bút xanh và đỏ, bút đỏ và tím, hoặc bút xanh và tím.
Giải bài 3 trang 107 Toán 6 tập 2 CTST
Lớp trưởng lớp 6A làm 4 tấm bia giống hệt nhau ghi tên 4 bạn hay hát trong lớp là Mai, Lan, Cúc, Trúc và cho vào một hộp. Một bạn trong lớp rút một trong 4 tấm bia đó và bạn có tên sẽ lên hát, sau đó tấm bia được trả lại hộp và cứ thế tiếp tục chọn người lên hát.
a) Liệt kê tập hợp các kết quả có thể xảy ra trong mỗi lần rút tấm bia.
b) Em có thể dự đoán trước được người tiếp theo lên hát không?
c) Có bạn nào phải lên hát nhiều lần không?
Bài giải:
a) Các kết quả có thể xảy ra trong mỗi lần rút tấm bìa là: Mai, Lan, Cúc, Trúc.
b) Không thể dự đoán trước được người tiếp theo lên hát vì xác suất rút phải tên đều như nhau.
c) Sẽ có bạn phải lên hát nhiều lần, vì sau mỗi lần rút tấm bìa được trả lại.
Giải bài 4 trang 107 Toán 6 tập 2 CTST
Trong hộp có 10 lá thăm được đánh số từ 0 đến 9. Lấy ra từ hộp 2 lá thăm. Trong các sự kiện sau, sự kiện nào chắc chắn xảy ra, sự kiện nào không thể xảy ra, sự kiện nào có thể xảy ra?
a) Tổng các số ghi trên hai lá thăm bằng 1.
b) Tích các số ghi trên hai lá thăm bằng 1.
c) Tích các số ghi trên hai lá thăm bằng 0.
d) Tổng các số ghi trên hai lá thăm lớn hơn 0.
Bài giải:
a) Tổng các số ghi trên hai lá thăm bằng 1: có thể xảy ra.
b) Tích các số ghi trên hai lá thăm bằng 1: không thể xảy ra.
c) Tích các số ghi trên hai lá thăm bằng 0: có thể xảy ra.
d) Tổng các số ghi trên hai lá thăm lớn hơn 0: chắc chắn xảy ra.
Giải bài 5 trang 107 Toán 6 tập 2 CTST
Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
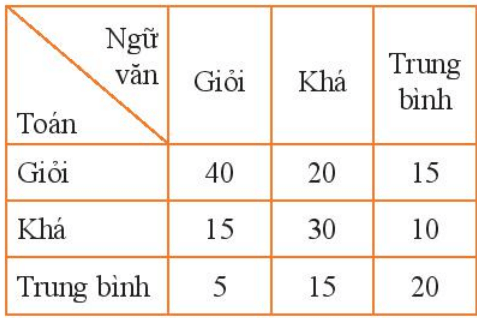
(Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – khá là 20).
Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
a) Môn Toán đạt loại giỏi;
b) Loại khá trở lên ở cả hai môn;
c) Loại trung bình ở ít nhất một môn.
Bài giải:
Tổng số học sinh là:
\(40 + 20 + 15 + 15 + 30 + 10 + 5 + 15 + 20 = 170\) (học sinh)
a) Xác suất thực nghiệm của sự kiện chọn ra học sinh môn Toán đạt loại giỏi là:
\((40 + 20 + 15):170 = \frac{{75}}{{170}} = \frac{{15}}{{34}}\)
b) Xác suất thực nghiệm của sự kiện học sinh được chọn đạt loại khá ở cả hai môn là:
\((40 + 15 + 20 + 30):170 = \frac{{105}}{{170}} = \frac{{21}}{{34}}\)
c) Xác suất thực nghiệm của sự kiện học sinh được chọn đạt loại trung bình ở ít nhất một môn là:
\((5 + 15 + 20 + 15 + 10):170 = \frac{{65}}{{170}} = \frac{{13}}{{34}}\).
Giải bài 6 trang 107 Toán 6 tập 2 CTST
Kiểm tra thị lực của học sinh một trường THCS, ta thu được bảng kết quả như sau:
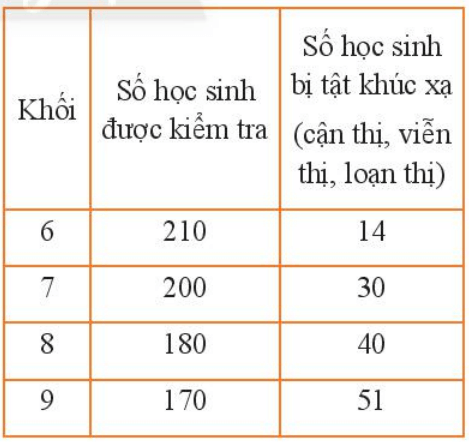
Hãy tính và so sánh xác suất thực nghiệm của sự kiện “học sinh bị tật khúc xạ” theo từng khối lớp.
Bài giải:
Xác suất thực nghiệm của sự kiện “học sinh bị tật khúc xạ” ở khối 6: \(\frac{14}{210} = \frac{2}{30}\)
Xác suất thực nghiệm của sự kiện “học sinh bị tật khúc xạ” ở khối 7: \(\frac{30}{200} = \frac{3}{{20}}\)
Xác suất thực nghiệm của sự kiện “học sinh bị tật khúc xạ” ở khối 8: \(\frac{40}{180} = \frac{2}{9}\)
Xác suất thực nghiệm của sự kiện “học sinh bị tật khúc xạ” ở khối 9: \(\frac{{51}}{{170}} = \frac{3}{10}\)
So sánh xác xuất thực nghiệm của sự kiện “học sinh bị tật khúc xạ”, ta thấy xác suất thực nghiệm của sự kiện “học sinh bị tật khúc xạ” tăng dần từ khối 6 đến khối 9.
⇒ Xác suất thực nghiệm của sự kiện “học sinh bị tật khúc xạ” ở khối 9 là lớn nhất.
Bài trước:
👉 HĐTH&TN: Xác suất thực nghiệm trong trò chơi may rủi sgk Toán 6 tập 2 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải Bài tập cuối chương 9 sgk Toán 6 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 6 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
