Nội Dung
Hướng dẫn giải Bài tập cuối chương III sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
GIẢI BÀI TẬP CUỐI CHƯƠNG III
Sau đây là phần Giải Bài tập cuối chương III trang 74 75 sgk Toán 8 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
A. TRẮC NGHIỆM
Giải bài 3.39 trang 74 Toán 8 tập 1 KNTT
Trong các khẳng định sau, khẳng định nào đúng?
A. Không có tứ giác nào mà không có góc tù.
B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.
C. Nếu tứ giác có hai góc tù thì góc còn lại phải nhọn.
D. Không có tứ giác nào có ba góc tù.
Bài giải:
♦ Khẳng định A: sai vì có xảy ra trường hợp tứ giác mà không có góc tù.
Chẳng hạn như hình chữ nhật có bốn góc vuông, tức là hình chữ nhật không có góc tù.
♦ Khẳng định B:
Tứ giác có ba góc nhọn thì tổng số đo của ba góc bé hơn: $90^o . 3 = 270^o.$
Khi đó, góc còn lại sẽ lớn hơn $360^o– 270^o= 90^o.$
Do đó, góc còn lại là góc tù nên khẳng định B đúng.
♦ Khẳng định C: sai vì có thể xảy ra trường hợp tứ giác có hai góc tù, một góc vuông và một góc nhọn.
Ví dụ:
Tứ giác $ABCD$ có \(\widehat A = {100^o}; \,\widehat B = {100^o}; \,\widehat C = {90^o}; \,\widehat D = {70^o}\).
♦ Khẳng định D: sai vì có thể xảy ra trường hợp tứ giác có ba góc tù.
Ví dụ:
Tứ giác $MNPQ$ có \(\widehat M = {100^o}; \,\widehat N = {110^o}; \,\widehat P = {120^o}; \,\widehat Q = {30^o}\).
Vậy khẳng định $B$ là đúng.
Giải bài 3.40 trang 74 Toán 8 tập 1 KNTT
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.
b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.
c) Tứ giác có ba góc vuông là hình chữ nhật.
d) Tứ giác có ba cạnh bằng nhau là hình thoi.
Bài giải:
♦ Khẳng định a): sai vì tứ giác có hai đường chéo bằng nhau thì chưa chắc tứ giác đó là hình bình hành.
♦ Khẳng định b): sai vì tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành, còn tứ giác có hai cặp cạnh bằng nhau thì chưa khẳng định được là hình bình hành.
♦ Khẳng định c): đúng.
Tứ giác có ba góc vuông thì số đo của góc còn lại là:
$360^o– 90^o . 3 = 90^o.$
Khi đó, số đo của góc còn lại cũng là góc vuông.
Do đó, tứ giác đã cho có bốn góc vuông nên tứ giác đó là hình chữ nhật.
♦ Khẳng định d): sai vì tứ giác có bốn cạnh bằng nhau mới là hình thoi.
Vậy khẳng định c) đúng; các khẳng định a), b), d) sai.
Giải bài 3.41 trang 74 Toán 8 tập 1 KNTT
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.
b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.
d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành.
Bài giải:
a) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Nên tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.
Do đó khẳng định a) đúng.
b) Hình bình hành có hai cặp cạnh đối diện bằng nhau.
Nên tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
Do đó khẳng định b) là đúng.
c) Tứ giác có hai cạnh song song là hình thang.
Hình thang có và hai đường chéo bằng nhau là hình thang cân.
Nên tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.
Do đó khẳng định c) đúng.
d) Tứ giác có hai cạnh đối vừa song song vừa bằng nhau là hình bình hành.
Do đó khẳng định d) sai.
Vậy các khẳng định a), b), c) đúng; khẳng định d) sai.
B. TỰ LUẬN
Giải bài 3.42 trang 74 Toán 8 tập 1 KNTT
Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân (H.3.59).

Bài giải:
Gọi $O$ là giao điểm của $AC$ và $BD$.

♦ Xét $∆ABC$ và $∆BAD$ có:
$AD = BC$ (giả thiết)
$AC = BD$ (giả thiết)
Cạnh $AB$ chung
Do đó $∆ABC = ∆BAD$ (c.c.c)
Suy ra \(\widehat {ADB} = \widehat {ACB}\) (hai góc tương ứng).
♦ Xét $∆ACD$ và $∆BDC$ có:
$AD = BC$ (giả thiết)
$AC = BD$ (giả thiết)
Cạnh $CD$ chung
Do đó $∆ADC = ∆BCD$ (c.c.c)
Suy ra \(\widehat {DAC} = \widehat {CB{\rm{D}}}\) (hai góc tương ứng).
♦ Xét ∆OAD và ∆OBC có:
\(\widehat {A{\rm{D}}B} = \widehat {ACB}\) (chứng minh trên)
$AD = BC$ (giả thiết)
\(\widehat {DAC} = \widehat {CB{\rm{D}}}\) (chứng minh trên)
Do đó $∆OAD = ∆OBC$ (g.c.g).
Suy ra $OA = OB; \,OC = OD$ (các cặp cạnh tương ứng).
Khi đó, các tam giác $OAB, OCD$ là tam giác cân tại $O$.
Suy ra \(\widehat {OAB} = \widehat {OBA}; \,\widehat {OCD} = \widehat {ODC}\)
♦ Xét $∆OAB$ và $∆OCD$ cân tại $O$ có:
• \(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
• \(\widehat {OAB} = \widehat {OBA}; \,\widehat {OCD} = \widehat {ODC}\)
• \(\widehat {OAB} + \widehat {OBA} + \widehat {AOB} = \widehat {OCD} + \widehat {OD} + \widehat {COD} = {180^o}\)
$\widehat {OAB} + \widehat {OBA} = \widehat {OCD} + \widehat {ODC}\\2\widehat {OAB} = 2\widehat {OCD}$
Suy ra \(\widehat {OAB} = \widehat {OCD}\) mà hai góc này ở vị trí so le trong.
Do đó $AB // CD$.
Tứ giác $ABCD$ có $AB // CD$ nên $ABCD$ là hình thang.
Hình thang $ABCD$ có hai đường chéo $AC = BD$.
Do đó tứ giác $ABCD$ là hình thang cân.
Vậy nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.
Giải bài 3.43 trang 74 Toán 8 tập 1 KNTT
Cho hình bình hành $ABCD$. Lấy điểm $P$ trên tia $AB$ sao cho $AP = 2 AB$.
a) Tứ giác $BPCD$ có phải là hình bình hành không? Tại sao?
b) Khi tam giác $ABD$ vuông cân tại $A$, hãy tính số đo các góc của tứ giác $BPCD$.
Bài giải:
Ta có hình vẽ minh họa sau:

a) Xét tứ giác $BPCD$ ta có:
$BP // CD, \,BP = CD$ (cùng bằng $AB$)
Suy ra $BPCD$ là hình bình hành.
b) Tam giác $ABD$ vuông cân tại $A$ suy ra $AB = AD$, do đó $ABCD$ là hình vuông
Khi đó $BD$ là phân giác $\widehat {ABC} ⇒ \widehat {DBC} = {45^o}$
$⇒ \widehat {DBP} = {45^o} + {90^o} = {135^o}$
⇒ \(\widehat {PCD} = \widehat {DBP} = {135^o}\)
Ta lại có:
$BD//PC ⇒\widehat {BPC} = \widehat {ABD} = {45^o}$ (hai góc đồng vị)
⇒ \(\widehat {BDC} = \widehat {BPC} = {45^o}\)
Vậy khi tam giác $ABD$ vuông cân tại $A$ thì số đo các góc của tứ giác $BPCD$ là \(\widehat {BDC} = \widehat {BPC} = {45^o}\), \(\widehat {PCD} = \widehat {DBP} = {135^o}\).
Giải bài 3.44 trang 75 Toán 8 tập 1 KNTT
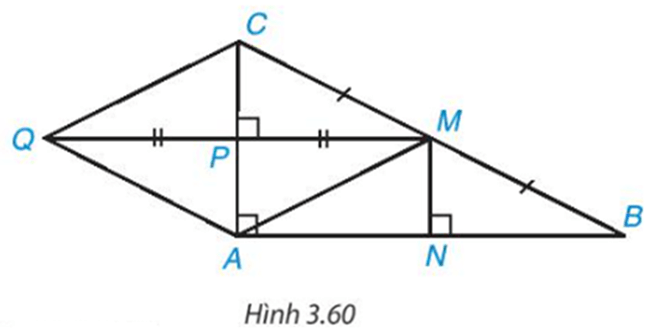
Cho tam giác $ABC$ vuông tại $A$. Gọi $M$ là trung điểm của $BC$ còn $P, N$ lần lượt là chân đường vuông góc hạ từ $M$ xuống $CA, AB$ (H.3.60).
a) Chứng minh hai tam giác vuông $CMP$ và $MBN$ bằng nhau.
b) Chứng minh tứ giác $APMN$ là một hình chữ nhật. Từ đó suy ra $N$ là trung điểm của $AB, P$ là trung điểm của $AC$.
c) Lấy điểm $Q$ sao cho $P$ là trung điểm của $MQ$, chứng minh rằng tứ giác $AMCQ$ là một hình thoi.
d) Nếu $AB = AC$, tức là tam giác $ABC$ vuông cân tại $A$ thì tứ giác $AMCQ$ có là hình vuông không? Vì sao?
Bài giải:
a) Ta có:
$MP⊥AC, AB⊥AC$
Suy ra $MP//AB$ nên \(\widehat {CMP} = \widehat B\)
Xét tam giác vuông $CMP$ và $MBN$ ta có:
$CM = MB$ (gt)
\(\widehat {CMP} = \widehat B\)
Suy ra $ΔCMP=ΔMBN$ (cạnh huyền – góc nhọn)
b) Xét tứ giác $APMN$ có:
\(\widehat P = \widehat A = \widehat N = {90^o}\)
Suy ra $APMN$ là hình chữ nhật
Xét tam giác $ABC$ có: $M$ là trung điểm $AB, MP//AB$ suy ra $P$ là trung điểm $AC$
Tương tự ta có: $M$ là trung điểm $AB, MN//AC$ suy ra $N$ là trung điểm $AB$
c) Xét tứ giác $AMCQ$ có:
$P$ là trung điểm $MQ$, $P$ là trung điểm $AC, AC⊥MQ$
Suy ra $AMCQ$ là hình thoi.
d) Nếu $ABC$ vuông cân tại $A , AM$ là đường trung tuyến suy ra $AM$ cũng là đường cao
Suy ra \(\widehat {AMC} = {90^o}\)
Xét hình thoi $AMCQ$ có \(\widehat {AMC} = {90^o}\)
Suy ra $AMCQ$ là hình vuông
Giải bài 3.45 trang 75 Toán 8 tập 1 KNTT
Cho tam giác $ABC$ cân tại $A$; $M$ là một điểm thuộc đường thẳng $BC, B$ ở giữa $M$ và $C$. Gọi $E$ và $K$ lần lượt là chân đường vuông góc hạ từ $M$ và từ $B$ xuống $AC$, còn $N, D$ lần lượt là chân đường vuông góc hạ từ $B$ xuống $ME$ và từ $M$ xuống $AB$(H.3.61).
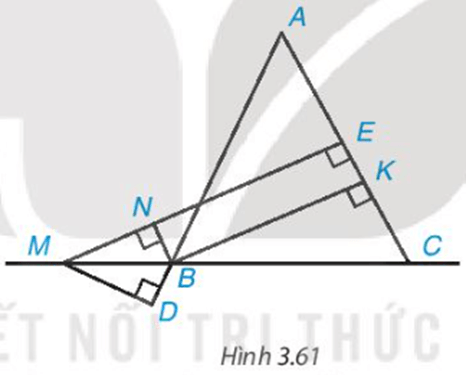
Chứng minh rằng:
a) Tứ giác $BKEN$ là hình chữ nhật.
b) $BK$ và $NE$ cùng bằng hiệu khoảng cách từ $M$ đến $AC$ và $AB$ (dù $M$ thay đổi trên đường thẳng $MC$ miễn là $B$ nằm giữa $M$ và $C$) tức là $BK = ME – MD$.
Bài giải:
a) Xét tứ giác $BKEN$ có:
\(\widehat {BKE} = \widehat {KEN} = \widehat {ENB} = {90^o}\)
Suy ra tứ giác $BKEN$ là hình chữ nhật.
b) $D$ là chân đường vuông góc hạ từ $M$ đến $AB$
Ta có $BN // AC$ (do $BKNE$ là hình chữ nhật)
Suy ra \(\widehat {MBN} = \widehat {BCA}\) (hai góc đồng vị)
\(\widehat {MBD} = \widehat {ABC}\) (đối đỉnh)
Mà \(\widehat {ABC} = \widehat {BCA}\) (tam giác $ABC$ cân tại $A$)
Suy ra \(\widehat {MBN} = \widehat {MBD}\)
Xét tam giác vuông $MBD$ và $MBN$ ta có:
$AB$ chung
\(\widehat {ABC} = \widehat {BCA}\)
Suy ra $ΔMBD = ΔMBN$ (cạnh huyền – góc nhọn)
Suy ra $MD = MN$
Lại có: $BK = NE = ME – MN$
Suy ra $BK = NE = ME − MD$
Bài trước:
👉 Giải bài 34 35 36 37 38 trang 73 sgk Toán 8 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 trang 80 sgk Toán 8 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải Bài tập cuối chương III trang 74 75 sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
