Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 trang 69 70 sgk Toán 7 tập 1 Cánh Diều

Nội Dung

Hướng dẫn giải Bài tập cuối chương II sgk Toán 7 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 trang 69 70 sgk Toán 7 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.

GIẢI BÀI TẬP CUỐI CHƯƠNG II

Sau đây là phần Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 trang 69 70 sgk Toán 7 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 trang 69 Toán 7 tập 1 CD

Tìm những số vô tỉ trong các số sau đây:

$-6,123(456); – \sqrt 4 ; \sqrt {\frac{4}{9}} ; \sqrt {11}; \sqrt{15}$.

Bài giải:

• Vì $-6,123(456)$ là số thập phân vô hạn tuần hoàn nên không là số vô tỉ.

• $ – \sqrt 4 = – 2$ không là số vô tỉ.

• $\sqrt {\frac{4}{9}} = \frac{2}{3}$ không là số vô tỉ.

• $\sqrt {11} $ là số vô tỉ vì không thể viết được dưới dạng $\dfrac{a}{b}(a,b \in \mathbb{Z},b \ne 0)$.

• $\sqrt {15} $ là số vô tỉ vì không thể viết được dưới dạng $\dfrac{a}{b}(a,b \in \mathbb{Z},b \ne 0)$.

Vậy trong các số trên có $\sqrt {11};\sqrt {15} $ là số vô tỉ.

Chú ý: Căn bậc hai của một số nguyên tố luôn là số vô tỉ.

Giải bài 2 trang 69 Toán 7 tập 1 CD

So sánh:

a) 4,9(18) và 4,928…;

b) -4,315 và -4,318..;

c) $\sqrt 3 $ và $\sqrt {\frac{7}{2}} $.

Bài giải:

a) $4,9(18) = 4,91818…< 4,928…$ (vì chữ số hàng phần trăm của 4,91818 là 1 nhỏ hơn chữ số hàng phần trăm của 4,928 là 2)

Vậy $4,9(18) < 4,928$

b) Vì $4,315 < 4,318…$ nên $-4,315 > -4,318…$

c) Vì 3 < $\frac{7}{2}$ nên $\sqrt 3 $ < $\sqrt {\frac{7}{2}} $

Giải bài 3 trang 69 Toán 7 tập 1 CD

a) Sắp xếp các số sau theo thứ tự tăng dần:

$6;\sqrt {35} ;\sqrt {47} ; – 1,7; – \sqrt 3 ;0$

b) Sắp xếp các số sau theo thứ tự giảm dần:

$ – \sqrt {2,3} ;\sqrt {5\frac{1}{6}} ;0;\sqrt {5,3} ; – \sqrt {2\frac{1}{3}} ; – 1,5$

Bài giải:

a) Ta có:

$6 = \sqrt {36} ; – 1,7 = – \sqrt {2,89} $

Vì $0 < 2,89 < 3$ nên $0> – \sqrt {2,89} > – \sqrt 3 $ hay $0 > -1,7 > – \sqrt 3$

Vì $0 < 35 < 36 < 47$ nên $0 < \sqrt {35} < \sqrt {36} < \sqrt {47} $ hay $0 < \sqrt {35} < 6 < \sqrt {47} $

Vậy các số theo thứ tự tăng dần là:

$ – \sqrt 3 ; – 1,7;0;\sqrt {35} ;6;\sqrt {47} $

b) Ta có:

$\sqrt {5\frac{1}{6}} = \sqrt {5,1(6)} ; – \sqrt {2\frac{1}{3}} = – \sqrt {2,(3)} $; -1,5 = $ – \sqrt {2,25} $

Vì 0 < 2,25 < 2,3 < 2,(3) nên 0> $ – \sqrt {2,25} > – \sqrt {2,3} > – \sqrt {2,(3)} $ hay 0 > -1,5 > $ – \sqrt {2,3} > – \sqrt {2\frac{1}{3}} $

Vì 5,3 > 5,1(6) > 0 nên $\sqrt {5,3} > \sqrt {5,1(6)} $> 0 hay $\sqrt {5,3} > \sqrt {5\frac{1}{6}} > 0$

Vậy các số theo thứ tự giảm dần là:

$\sqrt {5,3} ;\sqrt {5\frac{1}{6}} ;0$; -1,5; $ – \sqrt {2,3} ; – \sqrt {2\frac{1}{3}} $

Giải bài 4 trang 69 Toán 7 tập 1 CD

Tính:

a) $2.\sqrt 6 .( – \sqrt 6 )$;

b) $\sqrt {1,44} – 2.{(\sqrt {0,6} )^2}$;

c) $0,1.{(\sqrt 7 )^2} + \sqrt {1,69}$;

d) $( – 0,1).{(\sqrt {120} )^2} – \frac{1}{4}.{(\sqrt {20} )^2}$.

Bài giải:

a) Ta có:

$2.\sqrt 6 .( – \sqrt 6 ) = – 2.\sqrt 6 .\sqrt 6 \\ = – 2.{(\sqrt 6 )^2}\\ = – 2.6\\ = – 12$

b) Ta có:

$\sqrt {1,44} – 2.{(\sqrt {0,6} )^2}\\ = 1,2 – 2.0,6\\ = 1,2 – 1,2\\ = 0$$

c) Ta có:

$0,1.{(\sqrt 7 )^2} + \sqrt {1,69} \\ = 0,1.7 + 1,3 \\= 0,7 + 1,3 \\= 2$

d) Ta có:

$( – 0,1).{(\sqrt {120} )^2} – \frac{1}{4}.{(\sqrt {20} )^2} \\= ( – 0,1).120 – \frac{1}{4}.20\\ = – 12 – 5\\ = – (12 + 5)\\ = – 17$

Giải bài 5 trang 69 Toán 7 tập 1 CD

Tìm số x không âm, biết:

a) $\sqrt x – 16 = 0$;

b) $2\sqrt x = 1,5$;

c) $\sqrt {x + 4} – 0,6 = 2,4$.

Bài giải:

a) Ta có:

$\begin{array}{l}\sqrt x – 16 = 0\\⇔ \sqrt x = 16\\⇔x = {16^2}\\⇔ x = 256\end{array}$

Vậy $x = 256$.

b) Ta có:

$\begin{array}{l}2\sqrt x = 1,5\\⇔ \sqrt x = 1,5:2\\⇔ \sqrt x = 0.75\\⇔ x = {(0,75)^2}\\⇔ x = 0,5625\end{array}$

Vậy $x = 0,5625$.

c) Ta có:

$\begin{array}{l}\sqrt {x + 4} – 0,6 = 2,4\\⇔ \sqrt {x + 4} = 2,4 + 0,6\\ ⇔ \sqrt {x + 4} = 3\\⇔ x + 4 = 9\\⇔ x = 5\end{array}$

Vậy $x = 5$.

Giải bài 6 trang 69 Toán 7 tập 1 CD

Tìm số x trong các tỉ lệ thức sau:

a) $\frac{x}{{ – 3}} = \frac{7}{{0,75}}$;

b) $- 0,52:x = \sqrt {1,96} : ( – 1,5)$;

c) $x:\sqrt 5 = \sqrt 5 :x$

Bài giải:

a) Ta có:

$\begin{array}{l}\frac{x}{{ – 3}} = \frac{7}{{0,75}}\\ \Rightarrow x.0,75 = ( – 3).7\\ \Rightarrow x = \frac{{( – 3).7}}{{0,75}} = – 28\end{array}$

Vậy $x = 28 $

b) Ta có:

$\begin{array}{l} – 0,52:x = \sqrt {1,96} : ( – 1,5)\\ – 0,52:x = 1,3 : ( – 1,5)\\ – 0,52:x = – 1,95\\x = ( – 0,52):( – 1,95)\\x = \frac{4}{{15}}\end{array}$

Vậy $x = \frac{4}{{15}}$

c) Ta có:

$\begin{array}{l}x:\sqrt 5 = \sqrt 5 :x\\ \Leftrightarrow \frac{x}{{\sqrt 5 }} = \frac{{\sqrt 5 }}{x}\\ \Rightarrow x.x = \sqrt 5 .\sqrt 5 \\ \Leftrightarrow {x^2} = 5\\ \Leftrightarrow \left[ {_{x = – \sqrt 5 }^{x = \sqrt 5 }} \right.\end{array}$

Vậy $x \in \{ \sqrt 5 ; – \sqrt 5 \} $

Chú ý: Nếu ${x^2} = a(a > 0)$ thì x = $\sqrt a $ hoặc x = -$\sqrt a $

Giải bài 7 trang 69 Toán 7 tập 1 CD

Cho $\frac{a}{b} = \frac{c}{d}$ với $b – d \ne 0; b + 2d \ne 0$. Chứng tỏ rằng:

$\frac{{a – c}}{{b – d}} = \frac{{a + 2c}}{{b + 2d}}$

Bài giải:

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{a}{b} = \frac{c}{d} = \frac{{a – c}}{{b – d}}$; $\frac{a}{b} = \frac{c}{d} = \frac{{a + 2c}}{{b + 2d}}$

Như vậy $\frac{{a – c}}{{b – d}} = \frac{{a + 2c}}{{b + 2d}}$ (đpcm)

Giải bài 8 trang 69 Toán 7 tập 1 CD

Tìm ba số x, y, z biết: $\frac{x}{5} = \frac{y}{7} = \frac{z}{9}$ và x – y + z = $\frac{7}{3}$

Bài giải:

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\begin{array}{l}\frac{x}{5} = \frac{y}{7} = \frac{z}{9} = \frac{{x – y + z}}{{5 – 7 + 9}} = \frac{{\frac{7}{3}}}{7} = \frac{7}{3}.\frac{1}{7} = \frac{1}{3}\\ \Rightarrow x = 5.\frac{1}{3} = \frac{5}{3};\\y = 7.\frac{1}{3} = \frac{7}{3}\\z = 9.\frac{1}{3} = \frac{9}{3} = 3\end{array}$

Vậy $x = \frac{5}{3};y = \frac{7}{3};z = 3$

Giải bài 9 trang 69 Toán 7 tập 1 CD

Lớp 7A có 45 học sinh. Trong đợt sơ kết Học kì I, số học sinh ở các mức Tốt, Khá, Đạt tỉ lệ với ba số 3;4;2. Tính số học sinh ở mỗi mức, biết trong lớp không có học sinh nào ở mức Chưa đạt.

Bài giải:

Gọi số học sinh ở các mức Tốt, Khá, Đạt là $x, y, z (x,y,z \in \mathbb{N}$)

Vì lớp 7A có 45 học sinh và không có học sinh nào ở mức Chưa đạt nên $x+y+z =45$

Vì số học sinh ở các mức Tốt, Khá, Đạt tỉ lệ với ba số 3;4;2 nên $\frac{x}{3} = \frac{y}{4} = \frac{z}{2}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\begin{array}{l}\frac{x}{3} = \frac{y}{4} = \frac{z}{2} = \frac{{x + y + z}}{{3 + 4 + 2}} = \frac{{45}}{9} = 5\\ \Rightarrow x = 3.5 = 15\\y = 4.5 = 20\\z = 2.5 = 10\end{array}$

Vậy số học sinh ở các mức Tốt, Khá, Đạt lần lượt là: 15 bạn, 20 bạn và 10 bạn.

Giải bài 10 trang 70 Toán 7 tập 1 CD

Chị Phương định mua 3 kg táo với số tiền định trước. Khi vào siêu thị đúng thời điểm được khuyến mại nên giá táo được giảm 25%. Hỏi với số tiền đó, chị Phương mua được bao nhiêu ki-lô-gam táo?

Bài giải:

Gọi số táo mua được là $x (kg) (x > 0)$

Giả sử giá táo trước giảm giá là a thì giá táo sau khi giảm giá là: $a – 0,25a = 0,75a$

Vì số táo . giá táo = số tiền mua táo (không đổi) nên số táo và giá táo là hai đại lượng tỉ lệ nghịch.

Áp dụng tính chất của 2 đại lượng tỉ lệ nghịch, ta có:

$3.a = x. 0,75a$ nên $x = \frac{{3.a}}{{0,75.a}} = 4$ (thỏa mãn)

Vậy chị Phương mua được $4$ kg táo.

Giải bài 11 trang 70 Toán 7 tập 1 CD

Cứ 15 phút, chị Lan chạy được 2,5 km. Hỏi trong 1 giờ, chị chạy được bao nhiêu ki – lô- mét? Biết rằng vận tốc chạy của chị Lan là không đổi

Bài giải:

Gọi số km mà chị Lan chạy được trong 1 giờ = 60 phút là x (km) (x > 0)

Vì vận tốc không đổi nên quãng đường và thời gian là hai đại lượng tỉ lệ thuận nên theo tính chất của hai đại lượng tỉ lệ thuận, ta có:

$\frac{{2,5}}{{15}} = \frac{x}{{60}} \Rightarrow x = \frac{{2,5.60}}{{15}} = 10$ (thoả mãn)

Vậy trong $1$ giờ, chị Lan chạy được $10 km$

Giải bài 12 trang 70 Toán 7 tập 1 CD

Một công nhân trong 30 phút làm được 20 sản phẩm. Hỏi để làm được 50 sản phẩm người đó cần bao nhiêu phút? Biết năng suất làm việc của người đó không đổi.

Bài giải:

Gọi thời gian cần thiết để người đó làm được 50 sản phẩm là x (phút) ( x > 0)

Vì năng suất làm việc không đổi thì thời gian và số sản phẩm làm được là 2 đại lượng tỉ lệ thuận nên theo tính chất của hai đại lượng tỉ lệ thuận, ta có:

$\frac{{30}}{{x}} = \frac{{20}}{50} \Rightarrow x = \frac{{30.50}}{{20}} = 75$ (thỏa mãn)

Vậy để người đó làm được $50$ sản phẩm thì cần $75$ phút.

Giải bài 13 trang 70 Toán 7 tập 1 CD

Cứ đổi 1 158 000 đồng Việt Nam thì được 50 đô la Mỹ.

(Nguồn: https://portal.vietcombank.com.vn, cập nhật vào 18 giờ 30 phút ngày 07/5/2021)

Để có 750 đô la Mỹ thì cần đổi bao nhiêu đồng Việt Nam?

Bài giải:

Gọi số tiền Việt Nam cần có để đổi được 750 đô la Mỹ là x (đồng) (x >0)

Vì số tiền đô la Mỹ và số tiền Việt Nam quy đổi cho nhau là 2 đại lượng tỉ lệ thuận nên theo tính chất của 2 đại lượng tỉ lệ thuận, ta có:

$\frac{{1158000}}{{50}} = \frac{x}{{750}} \Rightarrow x = \frac{{1158000.750}}{{50}} = 17370000$ (thỏa mãn)

Vậy số tiền Việt Nam cần có để đổi được 750 đô la Mỹ là 17 370 000 đồng.

Giải bài 14 trang 70 Toán 7 tập 1 CD

Trong tháng trước, cứ 6 giờ, dây chuyền làm ra 1 000 sản phẩm. Nhưng trong tháng này, do được cải tiến nên năng suất của dây chuyền bằng 1,2 lần năng suất tháng trước. Hỏi trong tháng này để làm ra 1 000 sản phẩm như thế thì dây chuyền đó cần bao nhiêu thời gian?

Bài giải:

Gọi thời gian dây chuyền cần để hoàn thành 1 000 sản phẩm là x (giờ) (x > 0)

Giả sử năng suất của tháng trước là a thì năng suất của tháng này là $1,2.a$

Vì khối lượng công việc không đổi nên năng suất và thời gian hoàn thành là 2 đại lượng tỉ lệ nghịch nên theo tính chất của 2 đại lượng tỉ lệ nghịch, ta có:

$6.a = x. 1,2a$ nên $x = \frac{{6.a}}{{1,2.a}} = 5$ (thỏa mãn)

Vậy cần $5$ giờ để dây chuyền hoàn thành $1 000$ sản phẩm như thế

Giải bài 15 trang 70 Toán 7 tập 1 CD

Đồng trắng là một hợp kim của đồng với niken. Một hợp kim đồng trắng có khối lượng của đồng và niken tỉ lệ với 9 và 11. Tính khối lượng của đồng và niken cần dùng để tạo ra 25 kg hợp kim đó.

Bài giải:

Gọi khối lượng của đồng và niken cần dùng để tạo ra 25 kg hợp kim đó là $x, y (kg) (x, y > 0)$, ta có $x + y = 25$

Vì khối lượng của đồng và niken tỉ lệ với 9 và 11 nên $\frac{x}{9} = \frac{y}{{11}}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có

$\begin{array}{l}\frac{x}{9} = \frac{y}{{11}} = \frac{{x + y}}{{9 + 11}} = \frac{{25}}{{20}} = 1,25\\ \Rightarrow x = 9.1,25 = 11,25\\y = 11.1,25 = 13,75\end{array}$

Vậy cần $11,25 kg$ đồng và $13,75 kg$ niken.

Giải bài 16 trang 70 Toán 7 tập 1 CD

Cho ba hình chữ nhật có cùng diện tích. Biết chiều rộng của ba hình chữ nhật tỉ lệ với ba số 1;2;3. Tính chiều dài của mỗi hình chữ nhật đó, biết tổng chiều dài của ba hình chữ nhật là 110 cm.

Bài giải:

Gọi chiều dài 3 hình chữ nhật lần lượt là x, y, z (cm) (x, y, z > 0).

Do tổng chiều dài của ba hình chữ nhật là 110 cm nên $x+y+z=110$

Vì 3 hình chữ nhật có: chiều dài . chiều rộng = diện tích (không đổi) nên chiều rộng và chiều dài là 2 đại lượng tỉ lệ nghịch.

Áp dụng tính chất 2 đại lượng tỉ lệ nghịch, ta có:

$1.x = 2.y = 3.z$

$\begin{array}{l} \Rightarrow \frac{{1.x}}{6} = \frac{{2.y}}{6} = \frac{{3.z}}{6}\\ \Rightarrow \frac{x}{6} = \frac{y}{3} = \frac{z}{2}\end{array}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\begin{array}{l}\frac{x}{6} = \frac{y}{3} = \frac{z}{2} = \frac{{x + y + z}}{{6 + 3 + 2}} = \frac{{110}}{{11}} = 10\\ \Rightarrow x = 6.10 = 60;\\y = 3.10 = 30;\\z = 2.10 = 20\end{array}$

Vậy chiều dài của mỗi hình chữ nhật đó lần lượt là 60 cm, 30 cm, 20 cm.

Giải bài 17 trang 70 Toán 7 tập 1 CD

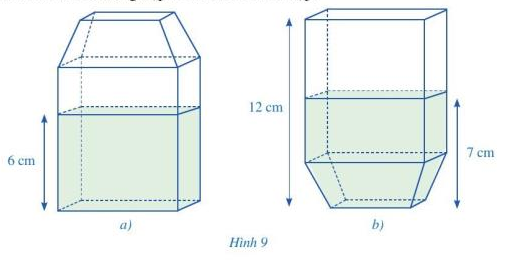
Hình 9a mô tả hình dạng của một hộp sữa và lượng sữa chứa trong hộp đó. Hình 9b mô tả hình dạng của một hộp sữa và lượng sữa chứa trong hộp khi đặt hộp ngược lại. Tính tỉ số của thể tích sữa có trong hộp và thể tích của cả hộp.

Bài giải:

Xét hình 9b, phần hộp không chứa sữa có dạng hình hộp chữ nhật với đáy là đáy của hộp sữa và chiều cao là 12 – 7 = 5 (cm)

Xét hình 9a, phần hộp chứa sữa có dạng hình hộp chữ nhật với đáy là đáy của hộp sữa và chiều cao là 6 cm.

Vì diện tích đáy không đổi thì thể tích và chiều cao của hình hộp là 2 đại lượng tỉ lệ thuận nên thể tích phần hộp không chứa sữa với phần hộp chứa sữa là tỉ lệ của chiều cao hình hộp không chứa sữa và chiều cao hình hộp có chứa sữa và là $\frac{5}{6}$. Tức là thể tích phần hộp chứa sữa là 6 phần, phần không chứa sữa là 5 phần, thể tích cả hộp là: 5+6 = 11 phần.

Như vậy, tỉ số của của thể tích sữa có trong hộp và thể tích của cả hộp là $\frac{6}{{11}}$

Bài trước:

👉 Giải bài 1 2 3 4 5 6 7 trang 68 sgk Toán 7 tập 1 Cánh Diều

Bài tiếp theo:

👉 HĐTH&TN: Chủ đề 1. Một số hình thức khuyến mãi trong kinh doanh sgk Toán 7 tập 1 Cánh Diều

Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 trang 69 70 sgk Toán 7 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“