Nội Dung
Hướng dẫn giải Bài tập cuối chương I sgk Toán 7 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 6 7 8 9 10 trang 30 31 sgk Toán 7 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
GIẢI BÀI TẬP CUỐI CHƯƠNG I
Sau đây là phần Giải bài 1 2 3 4 5 6 7 8 9 10 trang 30 31 sgk Toán 7 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 30 Toán 7 tập 1 CD
a) Sắp xếp các số sau theo thứ tự tăng dần: \(0,5;1;\dfrac{{ – 2}}{3}\).
b) Trong ba điểm A, B, C trên trục số dưới đây có một điểm biểu diễn số hữu tỉ 0,5. Hãy xác định điểm đó.

Bài giải:
a) Vì \(\dfrac{{ – 2}}{3} < 0\), mà 0 < 0,5 < 1 nên \(\dfrac{{ – 2}}{3} < 0,5 < 1\).
Vậy sắp xếp các số đã cho theo thứ tự tăng dần là: \(\frac{{ – 2}}{3};\,0,5;\,1\)
b) Số 0,5 nằm giữa số 0 và số 1
⇒ Điểm B biểu diễn số hữu tỉ $0,5$.
Giải bài 2 trang 30 Toán 7 tập 1 CD
Tính:
a) \(5\frac{3}{4}.\frac{{ – 8}}{9}\);
b) \(3\frac{3}{4}:2\frac{1}{2}\);
c) \(\frac{{ – 9}}{5}:\frac{1}{2}\);
d) \({\left( {1,7} \right)^{2023}}:{\left( {1,7} \right)^{2021}}\).
Bài giải:
a) Ta có:
\(5\frac{3}{4}.\frac{{ – 8}}{9} = \frac{{23}}{4}.\frac{{ – 8}}{9} = \frac{{ – 46}}{9}\);
b) Ta có:
\(3\frac{3}{4}:2\frac{1}{2} = \frac{{15}}{4}:\frac{5}{2} = \frac{{15}}{4}.\frac{2}{5} = \frac{3}{2}\)
c) Ta có:
\(\frac{{ – 9}}{5}:\frac{1}{2} = \frac{{ – 9}}{5}.2 = \frac{{ – 18}}{5}\)
d) Ta có:
\({\left( {1,7} \right)^{2023}}:{\left( {1,7} \right)^{2021}} = {\left( {1,7} \right)^{2023 – 2021}} = {\left( {1,7} \right)^2} = 2,89\).
Giải bài 3 trang 30 Toán 7 tập 1 CD
Tính một cách hợp lí:
a) \(\frac{{ – 5}}{{12}} + \left( { – 3,7} \right) – \frac{7}{{12}} – 6,3\);
b)\(2,8.\frac{{ – 6}}{{13}} – 7,2 – 2,8.\frac{7}{{13}}\).
Bài giải:
Ta tính như sau:
a) Ta có:
\(\begin{array}{l}\frac{{ – 5}}{{12}} + \left( { – 3,7} \right) – \frac{7}{{12}} – 6,3\\ = \left( {\frac{{ – 5}}{{12}} – \frac{7}{{12}}} \right) – \left( {3,7 + 6,3} \right)\\ = – 1 – 10 = – 11\end{array}\)
b) Ta có:
\(\begin{array}{l}2,8.\frac{{ – 6}}{{13}} – 7,2 – 2,8.\frac{7}{{13}}\\ = 2,8.\left( {\frac{{ – 6}}{{13}} – \frac{7}{{13}}} \right) – 7,2\\ = 2,8.\left( { – 1} \right) – 7,2\\ = – 2,8 – 7,2 = – 10\end{array}\)
Giải bài 4 trang 30 Toán 7 tập 1 CD
Tính:
a) \(0,3 – \frac{4}{9}:\frac{4}{3} \cdot \frac{6}{5} + 1\);
b) \({\left( {\frac{{ – 1}}{3}} \right)^2} – \frac{3}{8}:{(0,5)^3} – \frac{5}{2} \cdot ( – 4)\);
c) \(1 + 2:\left( {\frac{2}{3} – \frac{1}{6}} \right) \cdot ( – 2,25)\);
d) \(\left[ {\left( {\frac{1}{4} – 0,5} \right) \cdot 2 + \frac{8}{3}} \right]:2\).
Bài giải:
Ta tính như sau
a) Ta có:
\(\begin{array}{l}0,3 – \frac{4}{9}:\frac{4}{3} \cdot \frac{6}{5} + 1\\ = \frac{3}{{10}} – \frac{4}{9}.\frac{3}{4}.\frac{6}{5} + 1\\ = \frac{3}{{10}} – \frac{2}{5} + 1\\ = \frac{3}{{10}} – \frac{4}{{10}} + \frac{{10}}{{10}}\\ = \frac{9}{{10}}\end{array}\)
b) Ta có:
\(\begin{array}{l}{\left( {\frac{{ – 1}}{3}} \right)^2} – \frac{3}{8}:{(0,5)^3} – \frac{5}{2} \cdot ( – 4)\\ =\frac{1}{9} – \frac{3}{8}:(\frac{1}{2})^3 – \frac{5}{2}.\left( { – 4} \right)\\ = \frac{1}{9} – \frac{3}{8}:\frac{1}{8} – \frac{5}{2}.\left( { – 4} \right)\\ =\frac{1}{9} – \frac{3}{8}.8 – \frac{5}{2}.\left( { – 4} \right)\\ = \frac{1}{9} – 3 + 10\\ = \frac{1}{9} – \frac{{27}}{9} + \frac{{90}}{9}\\ = \frac{{64}}{9}\end{array}\)
c) Ta có:
\(\begin{array}{l}1 + 2:\left( {\frac{2}{3} – \frac{1}{6}} \right) \cdot ( – 2,25)\\ = 1 + 2:\left( {\frac{4}{6} – \frac{1}{6}} \right) \cdot \left( { – \frac{225}{100}} \right)\\ = 1 + 2:\frac{1}{2}.\left( { – \frac{9}{4}} \right)\\ = 1 + 2.\frac{2}{1}.\left( { – \frac{9}{4}} \right)\\ = 1 + \left( { – 9} \right) = – 8\end{array}\)
d) Ta có:
\(\begin{array}{l}\left[ {\left( {\frac{1}{4} – 0,5} \right) \cdot 2 + \frac{8}{3}} \right]:2\\ = \left[ {\left( {\frac{1}{4} – \frac{2}{4}} \right) \cdot 2 + \frac{8}{3}} \right].\frac{1}{2}\\ = \left( {\frac{{ – 1}}{4}.2 + \frac{8}{3}} \right).\frac{1}{2}\\ = \left( {\frac{{ – 1}}{2} + \frac{8}{3}} \right).\frac{1}{2}\\= \left( {\frac{{ – 3}}{6} + \frac{16}{6}} \right).\frac{1}{2}\\ = \frac{{13}}{6}.\frac{1}{2} = \frac{{13}}{{12}}\end{array}\).
Giải bài 5 trang 30 Toán 7 tập 1 CD
Tìm x, biết:
a) \(x + \left( { – \frac{2}{9}} \right) = \frac{{ – 7}}{{12}}\);
b) \(( – 0,1) – x = \frac{{ – 7}}{6}\)
c) \(( – 0,12) \cdot \left( {x – \frac{9}{{10}}} \right) = – 1,2\);
d) \(\left( {x – \frac{3}{5}} \right):\frac{{ – 1}}{3} = 0,4.\)
Bài giải:
Ta tìm $x$ như sau:
a) Ta có:
\(\begin{array}{l}x + \left( { – \frac{2}{9}} \right) = \frac{{ – 7}}{{12}}\\x = \frac{{ – 7}}{{12}} + \frac{2}{9}\\x = \frac{{ – 21}}{{36}} + \frac{8}{{36}}\\x = \frac{{ – 13}}{{36}}\end{array}\)
Vậy \(x = \frac{{ – 13}}{{36}}\).
b) Ta có:
\(\begin{array}{l}( – 0,1) – x = \frac{{ – 7}}{6}\\\frac{{ – 1}}{{10}} – x = \frac{{ – 7}}{6}\\x = \frac{{ – 1}}{{10}} + \frac{7}{6}\\x = \frac{{ – 3}}{{30}} + \frac{{35}}{{30}}\\x = \frac{{32}}{{30}}\\x = \frac{{16}}{{15}}\end{array}\)
Vậy \(x = \frac{{16}}{{15}}\)
c) Ta có:
\(\begin{array}{l}( – 0,12) \cdot \left( {x – \frac{9}{{10}}} \right) = – 1,2\\\frac{{ – 3}}{{25}} \cdot \left( {x – \frac{9}{{10}}} \right) = \frac{{ – 6}}{5}\\x – \frac{9}{{10}} = \frac{{ – 6}}{5}:\left( {\frac{{ – 3}}{{25}}} \right)\\x – \frac{9}{{10}} = \frac{{ – 6}}{5}.\frac{{ – 25}}{3}\\x – \frac{9}{{10}} = 10\\x = 10 + \frac{9}{{10}}\\x = \frac{{109}}{{10}}\end{array}\)
Vậy \(x = \frac{{109}}{{10}}\).
d) Ta có:
\(\begin{array}{l}\left( {x – \frac{3}{5}} \right):\frac{{ – 1}}{3} = 0,4\\\left( {x – \frac{3}{5}} \right):\frac{{ – 1}}{3} = \frac{2}{5}\\x – \frac{3}{5} = \frac{2}{5}.\frac{{ – 1}}{3}\\x – \frac{3}{5} = \frac{{ – 2}}{{15}}\\x = \frac{{ – 2}}{{15}} + \frac{3}{5}\\x= \frac{{ – 2}}{{15}} + \frac{9}{15}\\x = \frac{7}{{15}}\end{array}\)
Vậy \(x = \frac{7}{{15}}\).
Giải bài 6 trang 30 Toán 7 tập 1 CD
Sắp xếp các số sau theo thứ tự tăng dần:
a) \({(0,2)^0};{(0,2)^3};{(0,2)^1};{(0,2)^2};\)
b) \({( – 1,1)^2};{( – 1,1)^0};{( – 1,1)^1};{( – 1,1)^3}\).
Bài giải:
a) Ta có:
\({\left( {0,2} \right)^0} = 1;{\left( {0,2} \right)^1} = 0,2;{\left( {0,2} \right)^2} = 0,04;{\left( {0,2} \right)^3} = 0,008\)
Vì \(0,008 < 0, 04 < 0,2< 1\) nên sắp xếp các số theo thứ tự tăng dần là:
\({(0,2)^3};{(0,2)^2};{(0,2)^1};{(0,2)^0}.\)
b) Ta có:
\({\left( { – 1,1} \right)^0} = 1;{\left( { – 1,1} \right)^1} = – 1,1;{\left( { – 1,1} \right)^2} = 1,21;{\left( { – 1,1} \right)^3} = – 1,331\)
Vì \(-1,331 < -1,1 < 1 < 1,21\) nên sắp xếp các số theo thứ tự tăng dần là:
\({( – 1,1)^3};{( – 1,1)^1};{( – 1,1)^0};{( – 1,1)^2}\)
Chú ý:
– Nếu phần cơ số lớn hơn 1 thì khi số mũ tăng, giá trị lũy thừa cũng tăng.
– Nếu phần cơ số lớn hơn 0, nhỏ hơn 1 thì khi số mũ tăng giá trị lũy thừa giảm.
Giải bài 7 trang 30 Toán 7 tập 1 CD
Trọng lượng của một vật thể trên Mặt Trăng bằng khoảng \(\frac{1}{6}\) trọng lượng của nó trên Trái Đất. Biết trọng lượng của một vật trên Trái Đất được tính theo công thức: \(P = 10\;{\rm{m}}\) với \(P\) là trọng lượng của vật tính theo đơn vị Niu-tơn (kí hiệu \({\rm{N}}\)); \(m\) là khối lượng của vật tính theo đơn vị ki-lô-gam.
(Nguồn: Khoa học tự nhiên 6, NXB Đại học Sư phạm, 2021)
Nếu trên Trái Đất một nhà du hành vũ trụ có khối lượng là \(75,5\;{\rm{kg}}\) thì trọng lượng của người đó trên Mặt Trăng sẽ là bao nhiêu Niu-tơn (làm tròn kết quả đến hàng phần trăm)?
Bài giải:
Trọng lượng người đó trên Trái Đất là:
\(75,5.10 = 755 (N)\)
Trọng lượng người đó trên Mặt Trăng là:
\(755.\dfrac{1}{6} \approx 125,83\) (N)
Giải bài 8 trang 31 Toán 7 tập 1 CD
Một người đi quãng đường từ địa điểm \(A\) đến địa điểm \(B\) với vận tốc \(36\;{\rm{km}}/{\rm{h}}\) mất 3,5 giờ. Từ địa điểm \(B\) quay trở về địa điểm \(A\), người đó đi với vận tốc \(30\;{\rm{km}}/{\rm{h}}\). Tính thời gian đi từ địa điểm \(B\) quay trở về địa điểm \(A\) của người đó.
Bài giải:
Quãng đường AB dài: \(36.3,5 = 126\) (km)
Thời gian người đó đi quãng đường từ địa điểm B về địa điểm A là:
\(126:30 = \frac{{21}}{{5}}= 4,2\) (giờ) = 4 giờ 12 phút
Giải bài 9 trang 31 Toán 7 tập 1 CD
Một trường trung học cơ sở có các lớp 7A, 7B, 7C, 7D, 7E; mỗi lớp đều có 40 học sinh. Sau khi sơ kết Học kì I, số học sinh ở mức Tốt của mỗi lớp đó được thể hiện qua biểu đồ cột ở Hình 9.
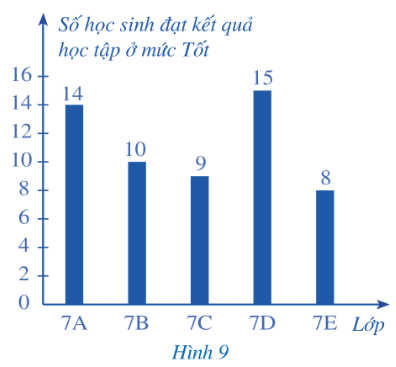
a) Lớp nào có số học sinh ở mức Tốt ít hơn một phần tư số học sinh của cả lớp?
b) Lớp nào có số học sinh ở mức Tốt nhiều hơn một phần ba số học sinh của cả lớp?
c) Lớp nào có tỉ lệ học sinh ở mức Tốt cao nhất, thấp nhất?
Bài giải:
a) Một phần tư số học sinh cả lớp là: \(\frac{1}{4}.40 = 10\) (học sinh).
⇒ Lớp 7C và 7E có số học sinh ở mức Tốt ít hơn một phần tư số học sinh của cả lớp.
b) Một phần ba số học sinh cả lớp là: \(\frac{1}{3}.40 \approx 13\)(học sinh).
⇒ Lớp 7A và 7D có số học sinh ở mức Tốt nhiều hơn một phần ba số học sinh của cả lớp.
c) Lớp 7D có tỉ lệ học sinh ở mức Tốt cao nhất.
Lớp 7E có tỉ lệ học sinh ở mức Tốt thấp nhất.
Giải bài 10 trang 31 Toán 7 tập 1 CD
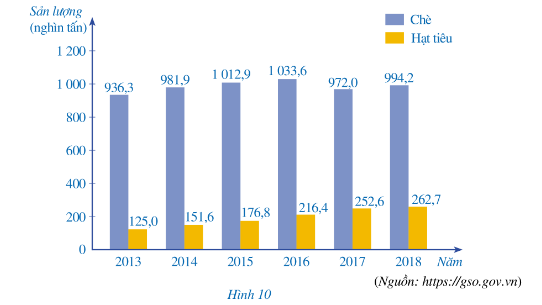
Sản lượng chè và hạt tiêu xuất khẩu của Việt Nam qua một số năm được biểu diễn trong biểu đồ cột kép ở Hình 10.
a) Những năm nào sản lượng chè xuất khẩu trên 1 triệu tấn? Sản lượng hạt tiêu xuất khẩu trên 0,2 triệu tấn?
b) Năm nào Việt Nam có sản lượng chè xuất khẩu lớn nhất? Sản lượng hạt tiêu xuất khẩu lớn nhất?
c) Tính tỉ số phần trăm của sản lượng chè xuất khẩu năm 2013 và sản lượng chè xuất khẩu năm 2018.
Bài giải:
a) Năm 2015 và năm 2016 sản lượng chè xuất khẩu trên 1 triệu tấn.
Năm 2016, 2017, 2018 sản lượng hạt tiêu xuất khẩu trên 0,2 triệu tấn.
b) Năm 2016 Việt Nam có sản lượng chè xuất khẩu lớn nhất.
Năm 2018 Việt Nam sản lượng hạt tiêu xuất khẩu lớn nhất.
c) Tỉ số phần trăm của sản lượng chè xuất khẩu năm 2013 và sản lượng chè xuất khẩu năm 2018 là:
\(\frac{{936,3}}{{994,2}}.100\% = 94,18\% \)
Bài trước:
👉 Giải bài 1 2 3 4 trang 29 sgk Toán 7 tập 1 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 trang 35 sgk Toán 7 tập 1 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 10 trang 30 31 sgk Toán 7 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
