Nội Dung
Hướng dẫn giải Bài tập cuối chương V sgk Toán 7 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 6 7 8 9 trang 34 35 36 sgk Toán 7 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
GIẢI BÀI TẬP CUỐI CHƯƠNG V
Sau đây là phần Giải bài 1 2 3 4 5 6 7 8 9 trang 34 35 36 sgk Toán 7 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 34 Toán 7 tập 2 CD
Biểu đồ cột ở Hình 33 biểu diễn kim ngạch xuất khẩu hàng hóa (ước đạt) của tỉnh Bình Dương vào các năm 2016, 2017, 2018, 2019, 2020.
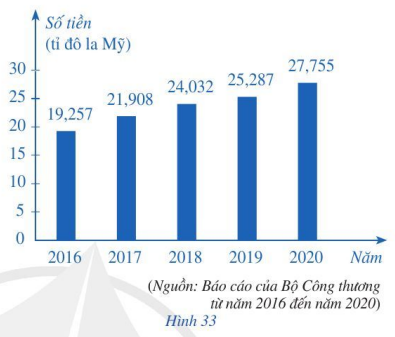
a) Kim ngạch xuất khẩu hàng hóa năm 2020 của tỉnh Bình Dương tăng bao nhiêu phần trăm so với năm 2016?
b) Trong giai đoạn từ năm 2016 đến năm 2020, kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương trung bình là bao nhiêu tỉ đô la Mỹ?
c) Hoàn thành số liệu ở bảng sau:
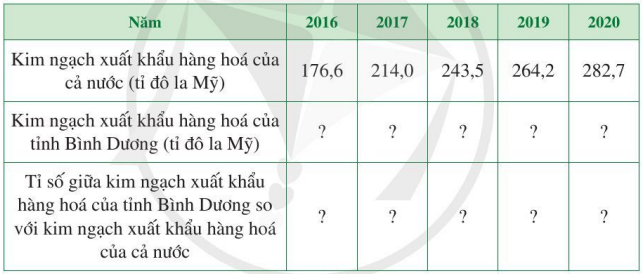
Bài giải:
a) Tỉ số phần trăm kim ngạch xuất khẩu hàng hóa năm 2020 và kim ngạch xuất khẩu hàng hóa năm 2016 là:
\(\dfrac{27,755}{19,257}.100 = 144,129 \approx 144,13 \%\)
Vậy kim ngạch xuất khẩu hàng hóa năm 2020 của tỉnh Bình Dương tăng 44,13% so với năm 2016.
b) Tổng kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương trong giai đoạn từ năm 2016 đến năm 2020 là:
\(19,257 + 21,908 + 24,032 + 25,287 + 27,755 = 118,239\) (tỉ đô la Mỹ)
Vậy trong giai đoạn từ năm 2016 đến năm 2020, kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương trung bình là:
\(118,239:5 = 23,6478\) (tỉ đô la Mỹ)
c) Tỉ số giữa kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hóa của cả nước năm 2016 là \(\dfrac{19,257}{176,6} \approx 0,11\).
Tương tự, ta có bảng số liệu:
| Năm | 2016 | 2017 | 2018 | 2019 | 2020 |
| Kim ngạch xuất khẩu hàng hóa của cả nước (tỉ đô la Mỹ) | 176,6 | 214,0 | 243,5 | 264,2 | 282,7 |
| Kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương (tỉ đô la Mỹ) | 19,257 | 21,908 | 24,032 | 25,287 | 27,755 |
| Tỉ số giữa kim ngạch xuất khẩu hàng hóa của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hóa của cả nước | \(\dfrac{19,257}{176,6}\)\(\) | \(\dfrac{21,908}{214,0}\) | \(\dfrac{24,032}{243,5}\) | \(\dfrac{25,287}{264,2}\) | \(\dfrac{27,755}{282,7}\) |
Giải bài 2 trang 34 Toán 7 tập 2 CD
Biểu đồ đoạn thẳng ở Hình 34 biểu diễn dân số của thế giới vào các năm 1804, 1927, 1959, 1974, 1987, 1999, 2011. Giả sử dân số thế giới tại các năm m và n (m < n) lần lượt là a và b. Ta gọi tốc độ tăng dân số từ năm m đến năm n là tỉ số \(\dfrac{b – a}{n – m}\).
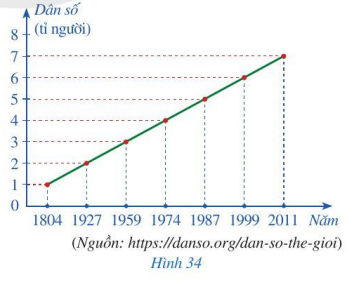
a) Tính tốc độ tăng dân số thế giới:
– Từ năm 1804 đến năm 1927;
– Từ năm 1999 đến năm 2011.
b) Tốc độ tăng dân số thế giới từ năm 1999 đến năm 2011 gấp bao nhiêu lần tốc độ tăng dân số thế giới từ năm 1804 đến năm 1927?
c) Hoàn thành số liệu ở bảng sau:

d) Nêu nhận xét về tốc độ tăng dân số thế giới từ năm 1804 đến năm 2011.
Bài giải:
a) Từ năm 1804 đến năm 1927:
Dân số thế giới tại các năm 1804 và 1927 lần lượt là 1 tỉ người và 2 tỉ người. Vậy tốc độ tăng dân số thế giới từ năm 1804 đến năm 1927 là:
\(\dfrac{2 – 1}{1927 – 1804} = 0,008\)
Tương tự, tốc độ tăng dân số thế giới từ năm 1999 đến năm 2011 là:
\(\dfrac{7 – 6}{2011 – 1999} = 0,08\)
b) Tốc độ tăng dân số thế giới từ năm 1999 đến năm 2011 gấp tốc độ tăng dân số thế giới từ năm 1804 đến năm 1927 là:
\(\dfrac{0,08}{0,008} = 10\) (lần)
c) Dân số thế giới tăng từ 1 tỉ người (năm 1804) lên 2 tỉ người (năm 1927) cần \(1927 – 1804 = 123\) (năm)
Tương tự, ta có bảng số liệu sau:
| Dân số thế giới tăng (tỉ người) | Từ 1 lên 2 | Từ 2 lên 3 | Từ 3 lên 4 | Từ 4 lên 5 | Từ 5 lên 6 | Từ 6 lên 7 |
| Thời gian cần thiết (năm) | 123 | 32 | 15 | 13 | 12 | 12 |
d) Nhận xét về tốc độ tăng dân số thế giới từ năm 1804 đến năm 2011:
– Tốc độ tăng dân số (tăng 1 tỉ người) ngày càng nhanh: từ 1 lên 2 tỉ người cần 123 năm (1804 – 1927), nhưng từ 2 lên 3 tỉ người chỉ cần 32 năm (1927 – 1959).
– Thời gian tăng dân số (1 tỉ người) ngày càng được rút ngắn (từ 123 năm xuống còn 12 năm).
Giải bài 3 trang 35 Toán 7 tập 2 CD
Theo kết quả tổng điều tra dân số và nhà ở năm 2019, dân số nước ta là 96 208 984 người và quy mô dân số theo sáu vùng kinh tế – xã hội được biểu diễn bằng biểu đồ hình quạt tròn ở Hình 35.
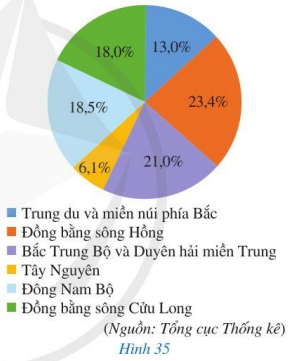
a) Nêu quy mô dân số của mỗi vùng kinh tế – xã hội của nước ta.
b) Vùng kinh tế – xã hội nào có quy mô dân số lớn nhất? Nhỏ nhất?
Bài giải:
a) Quy mô dân số của vùng Trung du và miền núi phía Bắc là:
\(\dfrac{96208984.13}{100} = 12507167,92\) (người)
Tương tự, quy mô dân số của vùng Đồng bằng sông Hồng, Bắc Trung Bộ và Duyên hải miền Trung, Tây Nguyên, Đông Nam Bộ, Đồng bằng sông Cửu Long lần lượt là:
\(\dfrac{96208984.23,4}{100} = 22512902,26\);
\(\dfrac{96208984.21}{100} = 20203886,64\);
\(\dfrac{96208984.6,1}{100} = 5868748,024\);
\(\dfrac{96208984.18,5}{100} = 17798662,04\);
\(\dfrac{96208984.18}{100} = 17317617,12\).
b) Ta thấy:
5 868 748,024 < 12 507 167,92 < 17 317 617,12 < 17 798 662,04 < 20 203 886,64 < 22 512 902,26
Vậy vùng kinh tế – xã hội Tây Nguyên là vùng có quy mô dân số nhỏ nhất (5 868 748,024 người) và vùng kinh tế – xã hội Đồng bằng sông Hồng là vùng có quy mô dân số lớn nhất (22 512 902,26 người).
Giải bài 4 trang 35 Toán 7 tập 2 CD
Biểu đồ ở Hình 36 biểu diễn tỉ lệ theo thể tích trong không khí của: khí oxygen; khí nitrogen; hơi nước, khí carbonic và các khí khác.
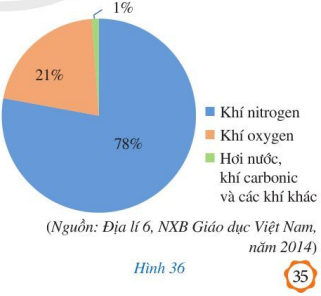
Quan sát biểu đồ các thành phân của không khí ở Hình 36 và cho biết trong không khí, có bao nhiêu phần trăm là:
a) Khí nitrogen;
b) Khí oxygen;
c) Hơi nước, khí carbonic và các khí khác.
Bài giải:
Quan sát biểu đồ ta thấy:
a) Khí nitrogen: 78%
b) Khí oxygen: 21%
c) Hơi nước, khí carbonic và các khí khác: 1%.
Giải bài 5 trang 36 Toán 7 tập 2 CD
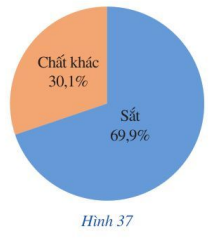
Quặng sắt là các loại đá và khoáng vật mà từ đó sắt kim loại có thể được chiết ra. Quặng sắt thường giàu các sắt oxit và có màu sắc từ xám sẫm, vàng tươi, tía sẫm tới nâu đỏ. Quặng hematite là loại quặng sắt chính có trong các mỏ quặng của nước Brasil. Tỉ lệ sắt trong quặng hematite được biểu diễn ở Hình 37. Trong 8 kg quặng hematite có bao nhiêu ki-lô-gam sắt?
Bài giải:
Quan sát biểu đồ ta thấy:
Trong 8 kg quặng hematite có số ki-lô-gam sắt là:
\(\dfrac{8.69,9}{100} = 5,592\) (ki-lô-gam).
Giải bài 6 trang 36 Toán 7 tập 2 CD
Gieo ngẫu nhiên xúc xắc một lần. Tính xác suất của mỗi biến cố sau:
a) “Mặt xuất hiện của xúc xắc có số chấm là ước của 6”.
b) “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 2”.
Bài giải:
Tập hợp gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là:
A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.
Số phần tử của tập hợp A là 6.
a) Có bốn kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước của 6” là: mặt 1 chấm, mặt 2 chấm, mặt 3 chấm, mặt 6 chấm.
Vì thế, xác suất của biến cố trên là \(\dfrac{4}{6} = \dfrac{2}{3}\).
b) Có hai kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 2” là: mặt 2 chấm, mặt 5 chấm.
Vì thế, xác suất của biến cố trên là \(\dfrac{2}{6} = \dfrac{1}{3}\).
Giải bài 7 trang 36 Toán 7 tập 2 CD
Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 51, 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số chia cho 17 dư 2 và chia cho 3 dư 1”.
b) “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5”.
Bài giải:
Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ rút ra là:
B = {1, 2, 3, …, 51, 52}.
Số phần tử của B là 52.
a) Trong các số từ 1 đến 52 có ba số chia 17 dư 2 là: 2, 19, 36. Trong 3 số trên, có một số chia 3 dư 1 là 19.
Vậy có một kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia cho 17 dư 2 và chia cho 3 dư 1” là: 19.
Vì thế, xác suất của biến cố trên là \(\dfrac{1}{52}\).
b) Có tám kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5” là: 5, 15, 25, 35, 45, 50, 51, 52.
Vì thế, xác suất của biến cố trên là \(\dfrac{8}{52} = \dfrac{2}{13}\).
Giải bài 8 trang 36 Toán 7 tập 2 CD
Viết ngẫu nhiên một số tự nhiên có hai chữ số. Tính xác suất của mỗi biến cố sau:
a) “Số tự nhiên được viết ra là số chia hết cho cả 2 và 5”;
b) “Số tự nhiên được viết ra là số có tổng các chữ số bằng 5”.
Bài giải:
Tập hợp C gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra là:
C = {10, 11, 12, …, 97, 98, 99}.
Số phần tử của C là 90
a) Có chín kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số chia hết cho cả 2 và 5” là: 10, 20, 30, 40, 50, 60, 70, 80, 90.
Vì thế, xác suất của biến cố trên là \(\dfrac{9}{90} = \dfrac{1}{10}\).
b) Có năm kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số có tổng các chữ số bằng 5” là: 14, 23, 32, 41, 50.
Vì thế, xác suất của biến cố trên là \(\dfrac{5}{90} = \dfrac{1}{18}\).
Giải bài 9 trang 36 Toán 7 tập 2 CD
Một đội thanh niên tình nguyện gồm 27 thành viên đến từ các tỉnh: Kom Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng, Phú Yên, Khánh Hòa, Ninh Thuận, Bình Thuận, Bà Rịa – Vũng Tàu, Bình Dương, Bình Phước, Đồng Nai, Tây Ninh, Long An, Tiền Giang, Vĩnh Long, Bến Tre, Đồng Tháp, Trà Vinh, An Giang, Cần Thơ, Hậu Giang, Bạc Liêu, Sóc Trăng, Kiên Giang, Cà Mau; mỗi tỉnh chỉ có đúng một thành viên trong đội. Chọn ra ngẫu nhiên một thành viên của đội thanh niên trên. Tính xác suất của mỗi biến cố sau:
a) “Thành viên được chọn ra đến từ vùng Tây Nguyên”;
b) “Thành viên được chọn ra đến từ vùng Duyên hải miền Trung”;
c) “Thành viên được chọn ra đến từ vùng Đông Nam Bộ”;
d) “Thành viên được chọn ra đến từ vùng Đồng bằng sông Cửu Long”.
Bài giải:
Tập hợp D gồm các kết quả có thể xảy ra đối với thành viên được chọn ra là từ các tỉnh:
D = {Kom Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng, Phú Yên, Khánh Hòa, Ninh Thuận, Bình Thuận, Bà Rịa – Vũng Tàu, Bình Dương, Bình Phước, Đồng Nai, Tây Ninh, Long An, Tiền Giang, Vĩnh Long, Bến Tre, Đồng Tháp, Trà Vinh, An Giang, Cần Thơ, Hậu Giang, Bạc Liêu, Sóc Trăng, Kiên Giang, Cà Mau}.
Số phần tử của D là 27.
a) Có năm kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Tây Nguyên” là: Kom Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng.
Vì thế, xác suất của biến cố trên là \(\dfrac{5}{27}\).
b) Có bốn kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Duyên hải miền Trung” là: Phú Yên, Khánh Hòa, Ninh Thuận, Bình Thuận.
Vì thế, xác suất của biến cố trên là \(\dfrac{4}{27}\).
c) Có năm kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Đông Nam Bộ” là: Bà Rịa – Vũng Tàu, Bình Dương, Bình Phước, Đồng Nai, Tây Ninh.
Vì thế, xác suất của biến cố trên là \(\dfrac{5}{27}\).
d) Có mười ba kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Đồng bằng sông Cửu Long” là: Long An, Tiền Giang, Vĩnh Long, Bến Tre, Đồng Tháp, Trà Vinh, An Giang, Cần Thơ, Hậu Giang, Bạc Liêu, Sóc Trăng, Kiên Giang, Cà Mau.
Vì thế, xác suất của biến cố trên là \(\dfrac{13}{27}\).
Bài trước:
👉 Giải bài 1 2 3 4 5 trang 32 33 sgk Toán 7 tập 2 Cánh Diều
Bài tiếp theo:
👉 HĐTH&TN: Dung tích phổi Toán 7 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 trang 34 35 36 sgk Toán 7 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
