Nội Dung
Hướng dẫn giải Bài 2. Số thực. Giá trị tuyệt đối của một số thực sgk Toán 7 tập 1 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 5 6 7 8 9 trang 38 sgk Toán 7 tập 1 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
BÀI 2. SỐ THỰC. GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ THỰC
Hoạt động khởi động trang 35 Toán 7 tập 1 CTST
Người ta gọi tập hợp các số hữu tỉ và số vô tỉ là gì?
Trả lời:
Người ta sẽ gọi tập gồm các số hữu tỉ và các số vô tỉ là tập số thực.
1. SỐ THỰC VÀ TẬP HỢP CÁC SỐ THỰC
Hoạt động khám phá 1 trang 35 Toán 7 tập 1 CTST
Trong các số sau, số nào là số hữu tỉ, số nào là số vô tỉ?
\(\frac{2}{3};\,\,\,\,3,\left( {45} \right);\,\,\,\,\sqrt 2 ;\,\,\, – 45;\,\,\, – \sqrt 3 ;\,\,\,0;\,\,\,\,\pi .\)
Trả lời:
Ta có: \(3,\left( {45} \right) = \frac{{38}}{{11}}\); \( – 45 = \frac{{ – 45}}{1};\,\,0 = \frac{0}{1}\) do đó:
Các số hữu tỉ là: \(\frac{2}{3};\,3,\left( {45} \right);\, – 45;\,0\).
Các số vô tỉ là: \(\sqrt 2 ;\, – \sqrt 3 ;\,\pi \).
Chú ý: Số thập phân vô hạn tuần hoàn cũng là số hữu tỉ.
Thực hành 1 trang 35 Toán 7 tập 1 CTST
Các phát biểu sau đúng hay sai? Nếu sai, hãy phát biểu lại cho đúng.
\(a)\,\sqrt 3 \in \mathbb{Q};\,\,\,\,\,\,\,b) \sqrt 3 \in \mathbb{R}\,\,\,\,\,c) \frac{2}{3} \notin \mathbb{R}\,\,\,\,\,d)\, – 9 \in \mathbb{R}\).
Trả lời:
a) \(\sqrt 3 \in \mathbb{Q}\) sai.
Sửa lại: \(\sqrt 3 \notin \mathbb{Q}\)
b) \(\sqrt 3 \in \mathbb{R}\) đúng.
c) \(\frac{2}{3} \notin \mathbb{R}\) sai.
Sửa lại: \(\frac{2}{3} \in \mathbb{R}\)
d) \( – 9 \in \mathbb{R}\) đúng.
2. THỨ TỰ TRONG TẬP HỢP CÁC SỐ THỰC
Hoạt động khám phá 2 trang 35 Toán 7 tập 1 CTST
Hãy so sánh các số thập phân sau đây: $3,14; 3,14(15); 3,141515$.
Trả lời:
Ta có: $3,14 < 3,141515 < 3,141515(15)$
Vậy $3,14 < 3,141515 < 3,14(15)$.
Thực hành 2 trang 36 Toán 7 tập 1 CTST
So sánh hai số thực:
a) 4,(56) và 4,56279;
b) -3,(65) và -3,6491;
c) 0,(21) và 0,2(12);
d) \(\sqrt 2 \) và 1,42.
Trả lời:
a) Ta có:
$4,(56)= 4,5656….$
Vì $4,5656… > 4,56279$ nên $4,(56) > 4,56279$
b) Ta có:
$-3,(65) = -3,6565…$
Vì $3,6565… > 3,6491$ nên $-3,6565…< -3,6491$. Do đó $-3,(65) < -3,6491$;
c) Ta có:
\(0,(21)=\frac{7}{{33}}\) và \(0,2(12)= \frac{7}{{33}}\) nên \(0,(21) = 0,2(12)\).
d) \(\sqrt 2 = 0,41421…< 1,42\).
Vận dụng 1 trang 36 Toán 7 tập 1 CTST
Cho một hình vuông có diện tích 5 m2. Hãy so sánh độ dài a của cạnh hình vuông đó với độ dài b = 2,361 m.
Trả lời:
Cạnh hình vuông có diện tích 5 m2 là:
\(a = \sqrt 5 = 2,236…\)(m)
Ta có: \(2,236… < 2,361\) nên $a<b$.
3. TRỤC SỐ THỰC
Hoạt động khám phá 3 trang 36 Toán 7 tập 1 CTST
Quan sát hình vẽ bên và cho biết độ dài của đoạn thẳng OA bằng bao nhiêu. Độ dài OA có là số hữu tỉ hay không?
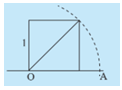
Trả lời:
Ta quan sát thấy hình vuông trong hình có độ dài cạnh là 1 nên độ dài đường chéo của nó là \(\sqrt 2 \). Mặt khác, ta thấy độ dài đường chéo của hình vuông bằng độ dài cạnh OA. Do đó độ dài cạnh OA = \(\sqrt 2 \).
Mà \(\sqrt 2 \) không phải số hữ tỉ nên $OA$ không phải số hữu tỉ.
Thực hành 3 trang 36 Toán 7 tập 1 CTST
Hãy biểu diễn các số thực: \( – 2;\,\, – \sqrt 2 ;\, – 1,5;\,\,2;\,3\) trên trục số.
Trả lời:
Ta biểu diễn các số thực: \( – 2;\,\, – \sqrt 2 ;\, – 1,5;\,\,2;\,3\) trên trục số như sau:

Vận dụng 2 trang 36 Toán 7 tập 1 CTST
Không cần vẽ hình, hãy nêu nhận xét về vị trí của hai số \(\sqrt 2 \,;\frac{3}{2}\) trên trục số.
Trả lời:
Do \(\sqrt 2 \, = 1,41… < \frac{3}{2} = 1,5\) nên số \(\sqrt 2 \) nằm bên trái số \(\frac{3}{2}\).
4. SỐ ĐỐI CỦA MỘT SỐ THỰC
Hoạt động khám phá 4 trang 37 Toán 7 tập 1 CTST

Gọi A và A’ lần lượt là hai điểm biểu diễn hai số 4,5 và -4,5 trên trục số. So sánh OA và OA’.
Trả lời:
Ta có: $OA = 4,5$ và $OA’=4,5$ nên $OA=OA’$.
Thực hành 4 trang 37 Toán 7 tập 1 CTST
Tìm số đối của các số thực sau: \(5,12;{\rm{ }}\pi ;{\rm{ }} – \sqrt {13} .\)
Trả lời:
Số đối của số: $5,12$ là $-5,12$
Số đối của số: \(\pi \) là \( – \pi \)
Số đối của số: \( – \sqrt {13} \) là \(\sqrt {13} \).
Chú ý: Muốn tìm số đối của một số ta chỉ cần đổi dấu của nó.
Vận dụng 3 trang 37 Toán 7 tập 1 CTST
So sánh các số đối của hai số \(\sqrt 2 \) và \(\sqrt 3 \).
Trả lời:
Số đối của hai số \(\sqrt 2 \) và \(\sqrt 3 \) lần lượt là \( – \sqrt 2 \) và \( – \sqrt 3 \)
Do \(2 < 3 \Rightarrow \sqrt 2 < \sqrt 3 \Rightarrow – \sqrt 2 > – \sqrt 3 \).
Chú ý: Với hai số thực a, b dương. Nếu a > b thì \(\sqrt a > \sqrt b \).
5. GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ THỰC
Hoạt động khám phá 5 trang 37 Toán 7 tập 1 CTST
Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm \(\sqrt 2 \) và \( – \sqrt 2 \).
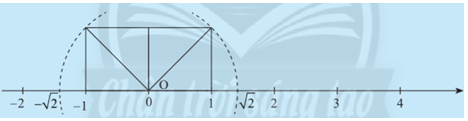
Trả lời:
Ta thấy khoảng cách từ 0 đến điểm \(\sqrt 2 \) bằng \(\sqrt 2 \).
Khoảng cách từ 0 đến điểm -\(\sqrt 2 \) bằng \(\sqrt 2 \)
Vậy khoảng cách từ 0 đến hai điểm \(\sqrt 2 \) và \( – \sqrt 2 \) bằng nhau.
Thực hành 5 trang 37 Toán 7 tập 1 CTST
Tìm giá trị tuyệt đối của các số thực sau: \(-3,14; 41; -5; 1,(2); -\sqrt5\).
Trả lời:
Ta có:
$\left| { – 3,14} \right| = 3,14$
${\rm{ }}\left| {41} \right| = 41$
${\rm{ }}\left| { – 5} \right| = 5$
${\rm{ }}\left| {1,\left( 2 \right)} \right| = 1,(2)$
${\rm{ }}\left| {- \sqrt 5} \right| = \sqrt 5.$
Vận dụng 4 trang 37 Toán 7 tập 1 CTST
Có bao nhiêu số thực x thoả mãn |x| = \(\sqrt 3 \)?
Trả lời:
Có hai số thực $x$ thỏa mãn là: \(x = \sqrt 3 ;\,\,x = – \sqrt 3 \).
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 7 8 9 trang 38 sgk Toán 7 tập 1 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 38 Toán 7 tập 1 CTST
Hãy thay mỗi ⍰ bằng kí hiệu \( \in \) hoặc \( \notin \) để có phát biểu đúng.
\(\begin{array}{l}5 ⍰ \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, – 2 ⍰ \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,\,\sqrt 2 ⍰ \mathbb{Q};\\\frac{3}{5} ⍰ \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,2,31\left( {45} \right) ⍰ I\,\,\,\,\,\,7,62\left( {38} \right) ⍰ \mathbb{R};\,\,\,\,0 ⍰ I\end{array}\).
Bài giải:
Ta thay như sau:
\(\begin{array}{l}5 \in \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, – 2 \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,\,\sqrt 2 \notin \mathbb{Q};\\\frac{3}{5} \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,2,31\left( {45} \right) \notin I\,\,\,\,\,\,7,62\left( {38} \right) \in \mathbb{R};\,\,\,\,0 \notin I\end{array}\)
Giải bài 2 trang 38 Toán 7 tập 1 CTST
Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn:
\(-\frac{2}{3};\,\,\,\,\,4,1;\,\,\, – \sqrt 2 ;\,\,\,\,3,2;\,\,\,\,\,\pi ;\,\,\,\, – \frac{3}{4};\,\,\,\,\frac{7}{3}.\)
Bài giải:
Ta có:
\(-\frac{2}{3} = -0,\left( 6 \right);\,\,\,\,\,4,1;\,\,\, – \sqrt 2 = – 1,414…;\,\,\,\,3,2;\,\,\,\,\,\\\pi = 3,141…;\,\,\,\, – \frac{3}{4} = – 0,75;\,\,\,\,\frac{7}{3} = 2,\left( 3 \right)\).
Do \( – 1,414… < – 0,75 < -0,\left( 6 \right) < 2,\left( 3 \right) < 3,141… < 3,2 < 4,1\)
Nên \( – \sqrt 2 < – \frac{3}{4} < -\frac{2}{3} < \frac{7}{3} < \pi < 3,2 < 4,1.\)
Giải bài 3 trang 38 Toán 7 tập 1 CTST
Hãy cho biết tính đúng, sai của các khẳng định sau:
a) \(\sqrt 2 ;\,\sqrt 3 ;\,\sqrt 5 \) là các số thực.
b) Số nguyên không là số thực.
c) \( – \frac{1}{2};\frac{2}{3};\, – 0,45\) là các số thực.
d) Số 0 vừa là số hữu tỉ vừa là số vô tỉ.
e) $1; 2; 3; 4$ là các số thực.
Bài giải:
a) \(\sqrt 2 ;\,\sqrt 3 ;\,\sqrt 5 \) là các số thực ⇒ Đúng.
b) Số nguyên không là số thực ⇒ Sai (Do Tất cả các số nguyên đều là số thực).
c) \( – \frac{1}{2};\frac{2}{3};\, – 0,45\) là các số thực ⇒ Đúng.
d) Số 0 vừa là số hữu tỉ vừa là số vô tỉ ⇒ Sai (Do số 0 không là số vô tỉ).
e) $1; 2; 3; 4$ là các số thực ⇒ Đúng.
Chú ý: Số thực là tập hợp số lớn nhất, bao gồm tất cả các tập hợp số đã được học.
Giải bài 4 trang 38 Toán 7 tập 1 CTST
Hãy thay ⍰ bằng các chữ số thích hợp.
a) 2,71467>2,7⍰932;
b) 5,17934<5,17⍰46.
Bài giải:
Ta thay như sau:
a) 2,71467>2,70932
b) 5,17934<5,17946 nên -5,17934>-5,17946
Giải bài 5 trang 38 Toán 7 tập 1 CTST
Tìm số đối của các số sau: \( – \sqrt 5 ;\,\,\,\,\,12,\left( 3 \right);\,\,\,\,0,4599;\,\,\,\,\,\sqrt {10} ;\,\,\,\, – \pi .\)
Bài giải:
Số đối của các số \( – \sqrt 5 ;\,\,\,\,\,12,\left( 3 \right);\,\,\,\,0,4599;\,\,\,\,\,\sqrt {10} ;\,\,\,\, – \pi \) lần lượt là: \(\sqrt 5 ;\,\,\,\,\, – 12,\left( 3 \right);\,\,\,\, – 0,4599;\,\,\,\,\, – \sqrt {10} ;\,\,\,\,\pi \).
Giải bài 6 trang 38 Toán 7 tập 1 CTST
Tìm giá trị tuyệt đối của các số sau: \( – \sqrt 7 ;\,\,\,\,\,52,\left( 1 \right);\,\,\,\,\,0,68;\,\,\,\,\,\, – \frac{3}{2};\,\,\,\,\,2\pi .\)
Bài giải:
Ta có:
$\left| { – \sqrt 7 } \right| = \sqrt 7$
$\left| {\,52,\left( 1 \right)} \right| = \,52,\left( 1 \right)$
$\left| {0,68} \right| = 0,68$
$\left| { – \frac{3}{2}} \right| = \frac{3}{2}$
$\left| {2\pi } \right| = 2\pi$.
Giải bài 7 trang 38 Toán 7 tập 1 CTST
Sắp xếp theo thứ tự từ nhỏ đến lớn giá trị tuyệt đối của các số sau:
\( – 3,2;\,\,\,\,\,2,13;\,\,\,\, – \sqrt 2 ;\,\,\,\, – \frac{3}{7}\).
Bài giải:
Ta có:
\(\left| { – 3,2} \right| = 3,2;\,\,\,\,\,\left| {2,13} \right| = 2,13;\\\left| {\, – \sqrt 2 } \right| = \sqrt 2 = 1,41..;\,\,\,\,\left| { – \frac{3}{7}} \right| = \frac{3}{7} = 0,42…\)
Do \(0,42 < 1,41… < 2,13 < 3,2\) nên:
\(\left| { – \frac{3}{7}} \right| < \left| { – \sqrt 2 } \right| < \left| {2,13} \right| < \left| { – 3,2} \right|\).
Giải bài 8 trang 38 Toán 7 tập 1 CTST
Tìm giá trị của x và y biết rằng: \(\left| x \right| = \sqrt 5 \) và \(\left| {y – 2} \right| = 0\).
Bài giải:
Ta có:
\(\left| x \right| = \sqrt 5 \Rightarrow x = \sqrt 5 \) hoặc \(x = – \sqrt 5 \)
\(\left| {y – 2} \right| = 0 \Rightarrow y – 2 = 0 \Rightarrow y = 2\).
Vậy \(x = \sqrt 5 \) hoặc \(x = – \sqrt 5 \), $y = 2$
Giải bài 9 trang 38 Toán 7 tập 1 CTST
Tính giá trị của biểu thức: \(M = \sqrt {\left| { – 9} \right|} \).
Bài giải:
Do \(\left| { – 9} \right| = 9\) nên ta có:
\(M = \sqrt {\left| { – 9} \right|} = \sqrt 9 = 3\)
Bài trước:
👉 Giải bài 1 2 3 4 5 6 7 8 trang 33 34 sgk Toán 7 tập 1 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 7 trang 42 sgk Toán 7 tập 1 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 trang 38 sgk Toán 7 tập 1 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
