Nội Dung
Hướng dẫn giải Bài §5. Tam giác đồng dạng sgk Toán 8 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 6 trang 73 sgk Toán 8 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
§5. TAM GIÁC ĐỒNG DẠNG
Câu hỏi khởi động trang 70 Toán 8 tập 2 CD
Trong bức ảnh ở Hình 46, các tam giác được tạo dựng với hình dạng giống hệt nhau nhưng có kích thước to nhỏ khác nhau.

Các tam giác trong Hình 46 gợi nên những tam giác có mối liên hệ gì?
Trả lời:
Các tam giác trong Hình 46 gợi nên những tam giác đồng dạng với nhau.
I. ĐỊNH NGHĨA
Hoạt động 1 trang 70 Toán 8 tập 2 CD
Cho tam giác $ABC$, điểm $M$ nằm trên cạnh $BC$. Gọi $A’, B’, C’$ lần lượt là trung điểm của các đoạn thẳng $MA, MB, MC$ (Hình 47).
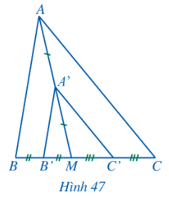
a) So sánh các cặp góc: \(\widehat {B’A’C’} \) và \(\widehat {BAC} \); \(\widehat {C’B’A’} \) và \(\widehat {CBA} \); \(\widehat {A’C’B’} \) và \(\widehat {ACB} \).
b) So sánh các tỉ số: \(\frac{A’B’}{AB} \); \(\frac{B’C’}{BC} \); \(\frac{C’A’}{CA} \).
Trả lời:
a) Xét tam giác $ABM$ có $A’B’$ là đường trung bình của tam giác
\(\Rightarrow A’B’ // AB\)
\(\Rightarrow \widehat {C’B’A’} = \widehat {CBA}\) (hai góc đồng vị)
Tương tự, tam giác $AMC$ có $A’C’$ là đường trung bình nên \(= \widehat {ACB}\) (hai góc đồng vị)
Xét tam giác $ABC$ có:
\(\widehat {BAC} + \widehat {CBA} + \widehat {ACB} = 180^0\)
Xét tam giác $A’B’C’$ có:
\(\widehat {B’A’C’} + \widehat {C’B’A’} + \widehat {A’C’B’} = 180^0\)
\(\Rightarrow \widehat {BAC} + \widehat {CBA} + \widehat {ACB} = \widehat {B’A’C’} + \widehat {C’B’A’} + \widehat {A’C’B’}\)
\(\Rightarrow \widehat {BAC} = \widehat {B’A’C’}\)
b) Ta có: $A’B’$ là đường trung bình của tam giác $ABM$ nên
\(A’B’ = \frac {1}{2} AB \Rightarrow \frac {A’B’}{AB} = \frac {1}{2}\)
$A’B’$ là đường trung bình của tam giác $ABM$ nên
\(A’C’ = \frac {1}{2} AC \Rightarrow \frac {A’C’}{AC} = \frac {1}{2}\)
Ta có:
\( \frac{B’C’}{BC} = \frac{MB’ +MC’}{2MB’ + 2MC’} = \frac{MB’ +MC’}{2(MB’ + MC’)} = \frac{1}{2}\)
\( \Rightarrow \frac{A’B’}{AB} = \frac{B’C’}{BC} = \frac{C’A’}{CA} \)
Luyện tập vận dụng 1 trang 71 Toán 8 tập 2 CD
Cho \(\Delta A’B’C’ \backsim \Delta ABC\) và \(AB = 3,\,\,BC = 2,\,\,CA = 4,\,\,A’B’ = x,\,\,B’C’ = 3,\,\,C’A’ = y\). Tìm \(x\) và \(y\).
Trả lời:
Vì $∆A’B’C’ᔕ ∆ABC$ nên $\frac {A’B’}{AB} = \frac {B’C’}{BC} = \frac {C’A’}{CA}$
Mà $BC = 2$ và $B’C’ = 3$ nên ta có:
$\frac {A’B’}{AB} = \frac {B’C’}{BC} = \frac {C’A’}{CA} = \frac {3′}{2}$
Do đó:
$x = A’B’ = \frac {3}{2} AB = \frac {3}{2}. 3= \frac {9}{2}$
$x = C’A’ = \frac {3}{2} CA = \frac {3}{2}. 4= 6$
Vậy \(x = \frac {9}{2}\) và \(y = 6\).
II. TÍNH CHẤT
Hoạt động 2 trang 71 Toán 8 tập 2 CD
Từ định nghĩa hai tam giác đồng dạng, hãy cho biết:
a) Mỗi tam giác có đồng dạng với chính nó hay không;
b) Nếu $∆A’B’C’$ đồng dạng với $∆ABC$ thì $∆ABC$ có đồng dạng với $∆A’B’C’$ hay không;
c) Nếu $∆A’’B’’C’’$ đồng dạng với $∆A’B’C’$ và $∆A’B’C’$ đồng dạng với $∆ABC$ thì $∆A’’B’’C’’$ có đồng dạng với $∆ABC$ hay không.
Trả lời:
a) Xét $∆ABC$ có: $\widehat A = \widehat A$; $\widehat B = \widehat B$; $\widehat C = \widehat C$ và $\frac {AB}{AB} = \frac {BC}{BC} = \frac {CA}{CA} = 1$ nên $∆ABC$ đồng dạng với chính nó.
b) Do $∆A’B’C’ᔕ ∆ABC$ nên
$\widehat {A’} = \widehat A$; $\widehat {B’} = \widehat B$; $\widehat {C’} = \widehat C$ và $\frac {A’B’}{AB} = \frac {B’C’}{BC} = \frac {C’A’}{CA}$
Suy ra:
$\widehat {A} = \widehat {A’}$; $\widehat {B} = \widehat {B’}$; $\widehat {C} = \widehat {C’}$ và $\frac {AB}{A’B’} = \frac {BC}{B’C’} = \frac {CA}{C’A’}$
Do đó $∆ABCᔕ ∆A’B’C’$.
c) Ta có:
$\frac {A”B”}{AB} = \frac {A”B”}{A’B’} . \frac {A’B’}{AB}$;
$\frac {B”C”}{BC} = \frac {B”C”}{B’C’} . \frac {B’C’}{BC}$;
$\frac {C”A”}{CA} = \frac {C”A”}{C’A’} . \frac {C’A’}{CA}$.
Do $∆A’’B’’C’’ᔕ ∆ A’B’C’$ nên:
$\widehat {A”} = \widehat {A’}$; $\widehat {B”} = \widehat {B’}$; $\widehat {C”} = \widehat {C’}$ và $\frac {A”B”}{A’B’} = \frac {B”C”}{B’C’} = \frac {C”A”}{C’A’}$
Do $∆A’B’C’ᔕ ∆ABC$ nên:
$\widehat {A’} = \widehat A$; $\widehat {B’} = \widehat B$; $\widehat {C’} = \widehat C$ và $\frac {A’B’}{AB} = \frac {B’C’}{BC} = \frac {C’A’}{CA}$
Suy ra
$\widehat {A”} = \widehat A$; $\widehat {B”} = \widehat B$; $\widehat {C”} = \widehat C$ và $\frac {A”B”}{AB} = \frac {B”C”}{BC} = \frac {C”A”}{CA}$
Do đó $∆A’’B’’C’’ ᔕ ∆ABC$.
Hoạt động 3 trang 72 Toán 8 tập 2 CD
Cho tam giác $ABC$ (Hình 50). Một đường thẳng song song với $BC$ cắt hai cạnh $AB, AC$ lần lượt tại $B’, C’$. Chứng minh $∆AB’C’ ᔕ ∆ABC$.
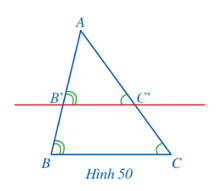
Trả lời:
Vì $B’C’ // BC$ nên ta có:
$\widehat {AB’C’} = \widehat {ABC}$ (hai góc đồng vị);
$\widehat {AC’B’} = \widehat {ACB}$ (hai góc đồng vị);
$\frac {AB’}{AB} = \frac {B’C’}{BC} = \frac {AC’}{AC}$ (hệ quả của định lí Thalès).
Xét $∆AB’C’$ và $∆ABC$ có:
$\widehat {B’AC’} = \widehat {BAC}$; $\widehat {AB’C’} = \widehat {ABC}$; $\widehat {AC’B’} = \widehat {ACB}$; $\frac {AB’}{AB} = \frac {B’C’}{BC} = \frac {AC’}{AC}$
Suy ra $∆AB’C’ᔕ ∆ABC$.
Luyện tập vận dụng 2 trang 72 Toán 8 tập 2 CD
Cho tam giác $ABC$. Gọi $B’, C’$ lần lượt là trung điểm của $AB, AC$. Chứng minh \(\Delta AB’C’ \backsim \Delta ABC\).
Trả lời:
Ta có hình vẽ minh họa sau:
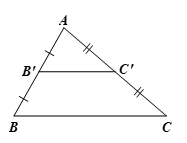
Ta có:
$B’, C’$ lần lượt là trung điểm của $AB, AC$ nên $B’C’$ là đường trung bình của tam giác $ABC$
\(\Rightarrow B’C’ // BC\)
Do đó \(\Delta A’B’C’ \backsim \Delta ABC\).
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 6 trang 73 sgk Toán 8 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 73 Toán 8 tập 2 CD
Cho \(\Delta ABC \backsim \Delta MNP\) và \(\widehat A = 45^\circ ,\,\,\widehat B = 60^\circ \). Tính các góc $C, M, N, P$.
Bài giải:
Ta có hình vẽ minh họa sau:
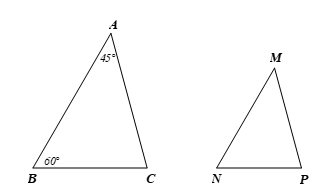
Vì \(\Delta ABC \backsim \Delta MNP\) nên:
\(\left\{ \begin{array}{l}\widehat A = \widehat M = 45^\circ \\\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P\end{array} \right.\)
Xét tam giác $ABC$ có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\45^\circ + 60^\circ + \widehat C = 180^\circ \\\widehat C = 180^\circ – 45^\circ – 60^\circ = 75^\circ \end{array}\)
\(\Rightarrow \widehat C = \widehat P = 75^\circ \)
Vậy $\widehat C = \widehat P = 75^\circ; \widehat M = 45^\circ; \widehat N = 60^\circ$.
Giải bài 2 trang 73 Toán 8 tập 2 CD
Cho \(\Delta ABC \backsim \Delta MNP\) và \(AB = 4,BC = 6,CA = 5,MN = 5\). Tính độ dài các cạnh $NP, PM$.
Bài giải:
Vì \(\Delta ABC \backsim \Delta MNP\) nên:
\(\begin{array}{l} \Rightarrow \frac{{AB}}{{MN}} = \frac{{BC}}{{NP}} = \frac{{CA}}{{PM}}\\ \Rightarrow \frac{4}{5} = \frac{6}{{NP}} = \frac{5}{{PM}}\\ \Rightarrow NP = \frac{{15}}{2};\,\,PM = \frac{{25}}{4}\end{array}\)
Vậy $NP = \frac{15}{2};\,\,PM = \frac{25}{4}$.
Giải bài 3 trang 73 Toán 8 tập 2 CD
Ba vị trí $A, B, C$ trong thực tiễn lần lượt được mô tả bởi ba đỉnh của tam giác $A’B’C’$ trên bản vẽ. Biết tam giác $A’B’C’$ đồng dạng với tam giác $ABC$ theo tỉ số \(\frac{1}{1\,000\,000}\) và \(A’B’ = 4cm,\,\,B’C’ = 5cm,\,\,C’A’ = 6cm\). Tính khoảng cách giữa hai vị trí $A$ và $B, B$ và $C, C$ và $A$ trong thực tiễn (theo đơn vị kilômét).
Bài giải:
Vì tam giác $A’B’C’$ đồng dạng với tam giác $ABC$ theo tỉ số \(\frac{1}{1\,000\,000}\) nên ta có:
\(\begin{array}{l}\frac{{A’B’}}{{AB}} = \frac{{B’C’}}{{BC}} = \frac{{A’C’}}{{AC}} = \frac{1}{{1\,000\,000}}\\ \Rightarrow \frac{4}{{AB}} = \frac{5}{{BC}} = \frac{6}{{AC}} = \frac{1}{{1\,000\,000}}\end{array}\)
Suy ra:
$AB = 4 \,000 \,000 \,cm = 40 \,km$.
$BC = 5 \,000 \,000 \,cm = 50 \,km$.
$AC = 6 \,000 \,000 \,cm = 60 \,km$.
Vậy khoảng cách giữa $A$ và $B$ là $40 \,km$, khoảng cách giữa $B$ và $C$ là $50 \,km$, khoảng cách giữa $C$ và $A$ là $60 \,km$.
Giải bài 4 trang 73 Toán 8 tập 2 CD
Trong Hình 54, độ rộng của khúc sông được tính bằng khoảng cách giữa hai vị trí $C, D$. Giả sử chọn được các vị trí $A, B, E$ sao cho \(\Delta ABE \backsim \Delta ACD\) và đo được \(AB = 20m,\,\,AC = 50m,\,\,BE = 8m\). Tính độ rộng của khúc sông đó.
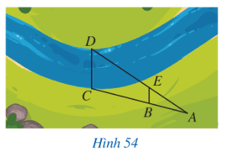
Bài giải:
Vì \(\Delta ABE \backsim \Delta ACD\) nên ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Leftrightarrow \frac{{20}}{{50}} = \frac{8}{{CD}} \Rightarrow CD = 8.50:20 = 20\)
Vậy độ rộng của khúc sông là $20 \,m$.
Giải bài 5 trang 73 Toán 8 tập 2 CD
Cho tam giác ABC (Hình 55), các điểm $M, N$ thuộc cạnh $AB$ thỏa mãn \(AM = MN = NB\), các điểm $P, Q$ thuộc cạnh $AC$ thỏa mãn \(AP = PQ = QC\). Tam giác $AMP$ đồng dạng với những tam giác nào?
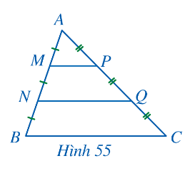
Bài giải:
Vì \(AM = MN = NB\) và \(AP = PQ = QC\) nên $M$ và $P$ lần lượt là trung điểm của $AN$ và $AQ$.
Khi đó $MP$ là đường trung bình của tam giác $ANQ$.
\(\begin{array}{l} \Rightarrow MP//NQ\\ \Rightarrow \Delta AMP \backsim \Delta ANQ\\ \Rightarrow \widehat {AMP} = \widehat {ANQ}\end{array}\)
Ta có:
\(\frac{{AM}}{{AB}} = \frac{{AP}}{{AC}} = \frac{1}{3} \Rightarrow MP//BC\) (Định lý Thales đảo)
\( \Rightarrow \Delta AMP \backsim \Delta ABC\).
Vậy tam giác $AMP$ đồng dạng với tam giác $ABC$.
Giải bài 6 trang 73 Toán 8 tập 2 CD
Cho hình bình hành $ABCD$. Một đường thẳng đi qua $D$ lần lượt cắt đoạn thẳng $BC$ và tia $AB$ tại $M$ và $N$ sao cho điểm $M$ nằm giữa hai điểm $B$ và $C$. Chứng minh:
a) \(\Delta NBM \backsim \Delta NAD\);
b) \(\Delta NBM \backsim \Delta DCM\);
c) \(\Delta NAD \backsim \Delta DCM\).
Bài giải:
Ta có hình vẽ minh họa sau:
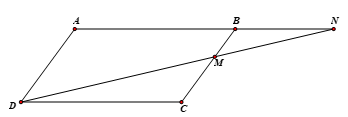
a) Vì $ABCD$ là hình bình hành nên \(AD//BC\) hay \(AD//BM\)
\(\Rightarrow \Delta NBM \backsim \Delta NAD\) (Định lý về cặp tam giác đồng dạng nhận dược từ định lý Thales)
b) Vì $ABCD$ là hình bình hành nên \(AB//CD\) hay \(BN//CD\)
\(\Rightarrow \Delta NBM \backsim \Delta DCM\) (Định lý về cặp tam giác đồng dạng nhận dược từ định lý Thales)
c) Ta có \(\Delta NBM \backsim \Delta NAD\) (chứng minh ở câu a)) và \(\Delta NBM \backsim \Delta DCM\) (chứng minh ở câu b)) nên \(\Delta NAD \backsim \Delta DCM\).
Bài trước:
👉 Giải bài 1 2 3 4 5 6 trang 69 sgk Toán 8 tập 2 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 trang 78 sgk Toán 8 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 6 trang 73 sgk Toán 8 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
