Giải bài 1 2 3 4 5 trang 111 sgk Toán 8 tập 1 Cánh Diều

---

II. TÍNH CHẤT

Hoạt động 2 trang 109 Toán 8 tập 1 CD

a) Mỗi hình chữ nhật có là một hình thang cân hay không?

b) Mỗi hình chữ nhật có là một hình bình hành hay không?

Trả lời:

a) Mỗi hình chữ nhật là một hình thang cân (do nó là hình thang có hai góc kề một đáy bằng nhau và bằng 90°).

b) Mỗi hình chữ nhật là một hình bình hành (do nó có hai cặp góc đối bằng nhau và cùng bằng 90°).

---

Luyện tập vận dụng 1 trang 110 Toán 8 tập 1 CD

Cho hình chữ nhật $ABCD$ có hai đường chéo $AC$ và $BD$ cắt nhau tại $O$. Gọi $M, N$ lần lượt là hình chiếu của $O$ trên $AB, BC$. Chứng minh: \(MN = \dfrac{1}{2}AC\).

Trả lời:

Ta có hình vẽ minh họa sau:

Do $ABCD$ là hình chữ nhật, $O$ là giao điểm của $AC$ và $BD$

Suy ra $OA = OB = OC = OD$

Xét tứ giác $MBNO$ có:

\(\widehat M = \widehat N = {90^o}\) (do $M, N$ lần lượt là hình chiếu của $O$ trên $AB, BC$)

\(\widehat B = {90^0}\)

nên $MBNO$ là hình chữ nhật.

Suy ra $MN = BO$ (tính chất hai đường chéo của hình chữ nhật)

\(⇒MN = \dfrac{1}{2}AC\) (do \(BO = AO = OC = \dfrac{1}{2}AC\)).

---

III. DẤU HIỆU NHẬN BIẾT

Hoạt động 3 trang 110 Toán 8 tập 1 CD

a) Cho hình bình hành $ABCD$ có \(\widehat A = {90^o}\). $ABCD$ có phải là hình chữ nhật hay không?

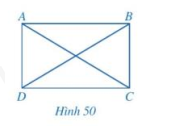
b) Cho hình bình hành $ABCD$ có hai đường chéo $AC$ và $BD$ bằng nhau (Hình 50).

• Hai tam giác $ABC$ và $DCB$ có bằng nhau hay không? Từ đó, hãy so sánh \(\widehat {ABC}\) và \(\widehat {DCB}\).

• $ABCD$ có phải là hình chữ nhật hay không?

Trả lời:

a) Hình bình hành $ABCD$ có \(\widehat A = {90^o}\)

Suy ra: \(\widehat C = \widehat A = {90^o}\)

Suy ra:

$\widehat B = \widehat D = \dfrac{360^o – \widehat A – \widehat C}{2}$ $= \dfrac{360^o – 90^o – 90^o}{2} = 90^o$

Vậy $ABCD$ là hình chữ nhật.

b) Xét hai tam giác $ABC$ và tam giác $DCB$ có:

$BC$ chung; $AB = DC$; $AC = BD$

Suy ra: \(\Delta ABC = \Delta DCB ⇒ \widehat {ABC} = \widehat {DCB}\)

Suy ra: \(\widehat {ABC} = \widehat {DCB} = \widehat {CBA} = \widehat {BAC} = {360^o}:4 = {90^o}\)

Vậy $ABCD$ là hình chữ nhật.

---

Luyện tập vận dụng 2 trang 111 Toán 8 tập 1 CD

Cho hình bình hành $ABCD$ có hai đường chéo $AC$ và $BD$ cắt nhau tại $O$ thỏa mãn \(\widehat {OAB} = \widehat {ODC}\). Chứng minh $ABCD$ là hình chữ nhật.

Trả lời:

Ta có hình vẽ minh họa sau:

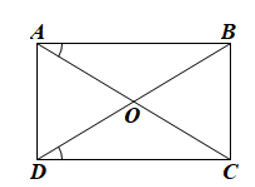
Do $ABCD$ là hình bình hành nên $AB // CD$ và $OA = OC; OB = OD$.

Mà tam giác $OCD$ cân tại $O$ suy ra $OC = OD$

$⇒ AC = BD$

Vậy hình bình hành $ABCD$ có hai đường chéo $AC = BD$ nên $ABCD$ là hình chữ nhật.

---

GIẢI BÀI TẬP

Sau đây là phần Giải bài 1 2 3 4 5 trang 111 sgk Toán 8 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 trang 111 Toán 8 tập 1 CD

Cho hình thang cân $ABCD$ có $AB // CD$, \(\widehat A = {90^o}\). Chứng minh $ABCD$ là hình chữ nhật.

Bài giải:

Ta có hình vẽ minh họa sau:

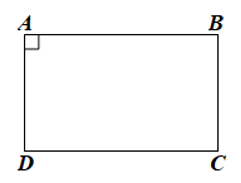
Hình thang cân $ABCD$ có $AB//CD$, \(\widehat A = 90^o\)

$⇒\widehat B = 90^0$ ⇒$\widehat C = \dfrac{360^o – 90^o – 90^o}{2} = 90^o$

Tứ giác $ABCD$ có 3 góc vuông nên $ABCD$ là hình chữ nhật.

---

Giải bài 2 trang 111 Toán 8 tập 1 CD

Cho tam giác $ABC$ vuông tại $A$ có $M$ là trung điểm của cạnh $BC$. Trên tia đối của tia $MA$ lấy điểm $D$ sao cho $MD = MA$. Chứng minh tứ giác $ABCD$ là hình chữ nhật và \(AM = \dfrac{1}{2}BC\).

Bài giải:

Ta có hình vẽ minh họa sau:

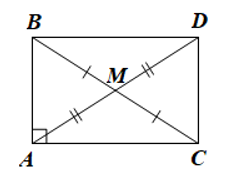
Xét tứ giác $ABCD$ có:

$MB = MC$ ($M$ là trung điểm của $BC$)

$MA = MD$ (gt)

Suy ra tứ giác $ABPC$ là hình bình hành (có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

Mà hình bình hành $ABDC$ có \(\widehat A = 90^o\) nên $ABCD$ là hình chữ nhật.

Vì $ABDC$ là hình chữ nhật nên $BC = AD$

Do đó \(AM = \dfrac{1}{2}AC = \dfrac{1}{2}BC\).

---

Giải bài 3 trang 111 Toán 8 tập 1 CD

Cho hình chữ nhật $ABCD$ có điểm $E$ nằm trên cạnh $CD$ sao cho \(\widehat {AEB} = {78^o}; \,\widehat {EBC} = {39^o}\). Tính số đo của \(\widehat {BEC}\) và \(\widehat {E{\rm{A}}B}\).

Bài giải:

Ta có hình vẽ minh họa sau:

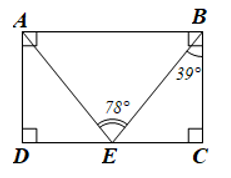
Xét tam giác BEC vuông tại C có:

$\widehat {BEC} + \widehat {EBC} + \widehat {BCE} = {180^o}$

$⇒ \widehat {BEC} + {39^o} + {30^o} = {180^o}$

$⇒ \widehat {BEC} = {180^o} – {39^o} – {30^o} = {51^o}$

Mà

$\widehat {EBA} + \widehat {EBC} = {90^o}$

⇒ $\widehat {EBA} = {90^o} – \widehat {EBC} = {90^o} – {39^o} = {51^o}$

Xét tam giác $AEB$ có:

$\widehat {AEB} + \widehat {EAB} + \widehat {EBA} = {180^o}$

$⇒\widehat {EAB} = {180^o} – \widehat {AEB} – \widehat {EBA} = {180^o} – {75^o} – {51^o} = {54^o}$.

---

Giải bài 4 trang 111 Toán 8 tập 1 CD

Một khu vườn có dạng tứ giác $ABCD$ với các góc $A, B, D$ là góc vuông, $AB = 400 m, AD = 300 m$. Người ta đã làm một cái hồ nước có dạng hình tròn, khi đó vị trí $C$ không còn nằm trong khu vườn nữa (Hình 52). Tính khoảng cách từ vị trí $C$ đến mỗi vị trí $A, B, D$.

Bài giải:

Tứ giác $ABCD$ có các góc $A, B, D$ là góc vuông nên tứ giác $ABCD$ là hình chữ nhật.

Khi đó:

$CD = AB = 400 m$

$CB = AD = 300 m$

Xét tam giác vuông $ABC$ vuông tại $B$ ta có:

$A{C^2} = A{B^2} + B{C^2} = {400^2} + {300^2} = 250000$

$⇒ AC = 500$ (m)

Vậy khoảng cách từ $C$ đến mỗi vị trí $A, B, D$ lần lượt là: $500m; 300m; 400m$.

---

Giải bài 5 trang 111 Toán 8 tập 1 CD

Bạn Linh có một mảnh giấy dạng hình tròn. Bạn Linh đó bạn Bình: làm thế nào có thể chọn ra 4 vị trí trên đường tròn đó để chúng là 4 đỉnh của một hình chữ nhật?

Bạn Bình làm như sau:

Bước 1: gấp mảnh giấy sao cho hai nửa đường tròn trùng khít nhau. Nét gấp thẳng tạo thành đường kính của hình tròn. Ta đánh dấu đầu mút của đường kính đó hai điểm A, C.

Bước 2: Sau đó lại gấp tương tự mảnh giấy đó nhưng theo đường kính mới và đánh dấu hai đầu mút của đường kính mới là hai điểm B, D. Khi đó tứ giác ABCD là hình chữ nhật (Hình 53).

Em hãy giải thích cách làm của bạn Bình.

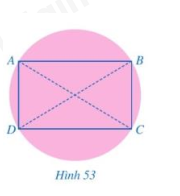
Bài giải:

Ta thấy $AC$ và $BD$ cắt nhau tại trung điểm của mỗi đường nên $ABCD$ là hình bình hành.

Mà $AC = BD$ nên hình bình hành $ABCD$ là hình chữ nhật.

---

Bài trước:

👉 Giải bài 1 2 3 4 5 trang 107 108 sgk Toán 8 tập 1 Cánh Diều

Bài tiếp theo:

👉 Giải bài 1 2 3 4 5 trang 115 sgk Toán 8 tập 1 Cánh Diều

Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 trang 111 sgk Toán 8 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!

---

“Bài tập nào khó đã có giaibaisgk.com“

---