Nội Dung
Hướng dẫn giải Bài §5. Tỉ lệ thức sgk Toán 7 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 trang 54 sgk Toán 7 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§5. TỈ LỆ THỨC
Câu hỏi khởi động trang 52 Toán 7 tập 1 CD
Có hai thanh sắt phi 18: thanh thứ nhất dài 2 m có khối lượng là 4 kg; thanh thứ hai dài 5 m có khối lượng là 10 kg.
Em có nhận xét gì về tỉ số giữa khối lượng của thanh sắt thứ nhất và khối lượng của thanh sắt thứ hai với tỉ số giữa chiều dài của thanh sắt thứ nhất và chiều dài của thanh sắt thứ hai?
Trả lời:
Tỉ số giữa khối lượng của thanh sắt thứ nhất và khối lượng của thanh sắt thứ hai là: \(\frac{4}{{10}} = \frac{2}{5}\)
Tỉ số giữa chiều dài của thanh sắt thứ nhất và chiều dài của thanh sắt thứ hai là: \(\frac{2}{5}\)
Như vậy, tỉ số giữa khối lượng của thanh sắt thứ nhất và khối lượng của thanh sắt thứ hai bằng tỉ số giữa chiều dài của thanh sắt thứ nhất và chiều dài của thanh sắt thứ hai
I. ĐỊNH NGHĨA
Hoạt động 1 trang 52 Toán 7 tập 1 CD
So sánh hai tỉ số \(\frac{{12}}{{28}}\) và \(\frac{{7,5}}{{17,5}}\)
Trả lời:
Ta có:
\(\begin{array}{l}\frac{{12}}{{28}} = \frac{{12:4}}{{28:4}} = \frac{3}{7};\\\frac{{7,5}}{{17,5}} = \frac{{75}}{{175}} = \frac{{75:25}}{{175:25}} = \frac{3}{7}\end{array}\)
Vậy \(\frac{{12}}{{28}}\) = \(\frac{{7,5}}{{17,5}}\).
Luyện tập vận dụng 1 trang 52 Toán 7 tập 1 CD
Từ các tỉ số sau đây có lập được tỉ lệ thức không?
a) \(\frac{{ – 2}}{5}:4\) và \(\frac{3}{4}:\frac{{ – 15}}{2}\);
b) \(\frac{{15}}{{27}}\) và $25:30$.
Trả lời:
a) Ta có:
\(\begin{array}{l}\frac{{ – 2}}{5}:4 = \frac{{ – 2}}{5}.\frac{1}{4} = \frac{{ – 2}}{{20}} = \frac{{ – 1}}{{10}};\\\frac{3}{4}:\frac{{ – 15}}{2} = \frac{3}{4}.\frac{{ – 2}}{{15}} = \frac{{ – 6}}{{60}} = \frac{{ – 1}}{{10}}\end{array}\)
Vậy \(\frac{{ – 2}}{5}:4\) và \(\frac{3}{4}:\frac{{ – 15}}{2}\) lập được tỉ lệ thức.
b) Ta có:
\(\begin{array}{l}\frac{{15}}{{27}} = \frac{{15:3}}{{27:3}} = \frac{5}{9};\\25:30 = \frac{{25}}{{30}} = \frac{{25:5}}{{30:5}} = \frac{5}{6}\end{array}\)
Vì \(\frac{5}{9} \ne \frac{5}{6}\) nên \(\frac{{15}}{{27}}\) và $25:30$ không lập được tỉ lệ thức.
II. TÍNH CHẤT
Hoạt động 2 trang 53 Toán 7 tập 1 CD
a) Cho tỉ lệ thức \(\frac{6}{{10}} = \frac{{ – 9}}{{ – 15}}\). So sánh tích hai số hạng 6 và -15 với tích hai số hạng 10 và -9.
b) Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Nhân hai vế của tỉ lệ thức với tích bd, ta được đẳng thức nào?
Trả lời:
a) Ta có: 6. (-15) = -90;
10.(-9) = – 90
Vậy tích hai số hạng 6 và -15 bằng tích hai số hạng 10 và -9.
b) Nhân hai vế của tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) với tích bd, ta được:
\(\frac{{a.b.d}}{b} = \frac{{c.b.d}}{d} \Rightarrow ad = bc\)
Vậy ta được đẳng thức $ad = bc$.
Luyện tập vận dụng 2 trang 53 Toán 7 tập 1 CD
Tìm số x trong tỉ lệ thức sau:
$(-0,4) : x = 1,2 : 0,3$.
Trả lời:
Vì $(-0,4) : x = 1,2 : 0,3$ nên:
\(\frac{{ – 0,4}}{x} = \frac{{1,2}}{{0,3}} \Rightarrow ( – 0,4).0,3 = 1,2.x \Rightarrow x = \frac{{( – 0,4).0,3}}{{1,2}} = – 0,1\)
Vậy $x = – 0,1$
Hoạt động 3 trang 53 Toán 7 tập 1 CD
Ta có đẳng thức $4 : 9 = 3 . 12$
a) Viết kết quả dưới dạng tỉ lệ thức khi chia hai vế của đẳng thức trên cho 9.3.
b) Tìm số thích hợp cho ⍰.
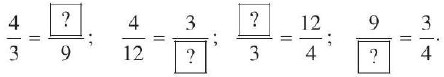
Trả lời:
a) Ta chia cả hai vế của đẳng thức $4.9 = 3.12$ cho $9.3$ ta được:
\(\frac{4.9}{9.3} = \frac{3.12}{9.3}\)
Rút gọn tử với mẫu ta được \(\frac{4}{3} = \frac{12}{9}\).
b) Ta điền số như sau:
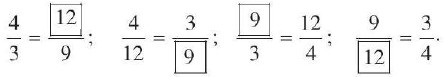
Luyện tập vận dụng 3 trang 54 Toán 7 tập 1 CD
a) Đưa hai số 21 và 27 vào ⍰ cho thích hợp:
18 . ⍰ = ⍰ . 14
b) Lập tất cả các tỉ lệ thức có thể được từ bốn số sau:
14; 18; 21; 27.
Trả lời:
a) Ta được: $18 . 21 = 27 . 14$.
b) Từ 4 số: 14; 18; 21; 27, ta có đẳng thức sau: $18 . 27 = 21 . 14$, ta lập được các tỉ lệ thức:
\(\frac{{18}}{{27}} = \frac{{14}}{{21}}; \frac{{18}}{{14}} = \frac{{27}}{{21}}; \frac{{14}}{{18}} = \frac{{21}}{{27}}; \frac{{21}}{{14}} = \frac{{27}}{{18}}\).
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 trang 54 sgk Toán 7 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 54 Toán 7 tập 1 CD
Từ các tỉ số sau đây có lập được tỉ lệ thức không?
a) 3,5 : (-5,25) và (-8) : 12;
b) \(39\frac{3}{{10}}:52\frac{2}{5}\) và 7,5 : 10;
c) 0,8 : (-0,6) và 1,2 : (-1.8)
Bài giải:
a) Ta có:
\(\begin{array}{l}3,5{\rm{ }}:{\rm{ }}\left( { – 5,25} \right) = \frac{{3,5}}{{ – 5,25}} = \frac{{350}}{{ – 525}} = \frac{{350:( – 175)}}{{( – 525):( – 175}} = \frac{{ – 2}}{3};\\( – 8):12 = \frac{{ – 8}}{{12}} = \frac{{( – 8):4}}{{12:4}} = \frac{{ – 2}}{3}\end{array}\)
Vậy từ các tỉ số 3,5 : (-5,25) và (-8) : 12 lập được tỉ lệ thức.
b) Ta có:
\(\begin{array}{l}39\frac{3}{{10}}:52\frac{2}{5} = \frac{{393}}{{10}}:\frac{{262}}{5} = \frac{{393}}{{10}}.\frac{5}{{262}} = \frac{3}{4};\\7,5:10 = \frac{{7,5}}{{10}} = \frac{{75}}{{100}} = \frac{{75:25}}{{100:25}} = \frac{3}{4}\end{array}\)
Vậy từ các tỉ số \(39\frac{3}{{10}}:52\frac{2}{5}\) và 7,5 : 10 lập được tỉ lệ thức.
c) Ta có:
\(\begin{array}{l}0,8{\rm{ }}:{\rm{ }}\left( { – 0,6} \right) = \frac{{0,8}}{{ – 0,6}} = \frac{8}{{ – 6}} = \frac{{8:( – 2)}}{{( – 6):( – 2)}} = \frac{{ – 4}}{3};\\1,2:( – 1,8) = \frac{{1,2}}{{ – 1,8}} = \frac{{12}}{{ – 18}} = \frac{{12:( – 6)}}{{( – 18):( – 6)}} = \frac{{ – 2}}{3}\end{array}\)
Vì \(\frac{{ – 4}}{3} \ne \frac{{ – 2}}{3}\) nên từ các tỉ số $0,8 : (-0,6) và 1,2 : (-1.8)$ không lập được tỉ lệ thức.
Giải bài 2 trang 54 Toán 7 tập 1 CD
Tìm x trong mỗi tỉ lệ thức sau:
a) \(\frac{x}{5} = \frac{{ – 2}}{{1,25}}\);
b) $18 : x = 2,4 : 3,6$;
c) $(x+1) : 0,4 = 0,5 : 0,2$.
Bài giải:
a) Ta có: x . 1,25 = 5. (-2) nên \(x = \frac{{5.( – 2)}}{{1,25}} = – 8\)
Vậy $x = -8$
b) Vì 18 : x = 2,4 : 3,6 nên \(\frac{{18}}{x} = \frac{{2,4}}{{3,6}} \Rightarrow 18.3,6 = x.2,4 \Leftrightarrow x = \frac{{18.3,6}}{{2,4}} = 2\)
Vậy $x = 2$
c) Vì (x+1) : 0,4 = 0,5 : 0,2 nên \(\frac{{x + 1}}{{0,4}} = \frac{{0,5}}{{0,2}} \Rightarrow (x + 1).0,2 = 0,4.0,5 \Leftrightarrow x + 1 = \frac{{0,4.0,5}}{{0,2}} = 1 \Leftrightarrow x = 0\)
Vậy $x = 0$
Giải bài 3 trang 54 Toán 7 tập 1 CD
Lập tất cả các tỉ lệ thức có thể có được từ bốn số sau: $1,5; 2; 3,6; 4,8$.
Bài giải:
Từ 4 số: $1,5; 2; 3,6; 4,8$ ta có đẳng thức sau: $1,5 . 4,8 = 2. 3,6$
Ta lập được các tỉ lệ thức như sau:
\(\frac{{1,5}}{2} = \frac{{3,6}}{{4,8}};\frac{{1,5}}{{3,6}} = \frac{2}{{4,8}};\frac{{4,8}}{2} = \frac{{3,6}}{{1,5}};\frac{{4,8}}{{3,6}} = \frac{2}{{1,5}}\)
Giải bài 4 trang 54 Toán 7 tập 1 CD
Trong giờ thí nghiệm xác định trọng lượng, bạn Hà dùng hai quả cân 100 g và 50 g thì đo được trọng lượng tương ứng là 1 N và 0,5 N.
a) Tính tỉ số giữa khối lượng của quả cân thứ nhất và khối lượng của quả cân thứ hai; tỉ số giữa trọng lượng tương ứng của quả cân thứ nhất và trọng lượng của quả cân thứ hai.
b) Hai tỉ số trên có lập thành tỉ lệ thức không?
Bài giải:
a) Tỉ số giữa khối lượng của quả cân thứ nhất và khối lượng của quả cân thứ hai là:
\(\frac{{100}}{{50}} = \frac{2}{1}\)
Tỉ số giữa trọng lượng tương ứng của quả cân thứ nhất và trọng lượng của quả cân thứ hai là:
\(\frac{1}{{0,5}} = \frac{2}{1}\)
b) Vì hai tỉ số trên bằng nhau nên lập thành tỉ lệ thức.
Giải bài 5 trang 54 Toán 7 tập 1 CD
Người ta pha nhiên liệu cho một loại động cơ bằng cách trộn 2 phần dầu với 7 phần xăng. Hỏi cần bao nhiêu lít xăng để trộn hết 8 lít dầu theo cách pha nhiên liệu như trên?
Bài giải:
Gọi số lít xăng cần để trộn là $x (x > 0)$
Vì số lít dầu: số lít xăng = 2 : 7 nên 8 : x = 2 : 7
Hay \(\frac{8}{x} = \frac{2}{7} \Rightarrow 8.7 = 2.x \Rightarrow x = \frac{{8.7}}{2} = 28\)
Vậy cần $28$ lít xăng để trộn hết $8$ lít dầu theo cách pha nhiên liệu như trên.
Bài trước:
👉 Giải bài 1 2 3 4 5 trang 51 sgk Toán 7 tập 1 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 7 trang 58 sgk Toán 7 tập 1 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 trang 54 sgk Toán 7 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
